江苏省无锡市惠山区2023年中考三模数学试题
试卷更新日期:2023-07-17 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、42. 下列图案中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 若正多边形的一个外角的度数为45°,则这个正多边形是( )A、正五边形 B、正六边形 C、正八边形 D、正十边形5. 在九年级体育中考中,某校某班参加仰卧起坐测试的一组女生(每组8人)测试成绩如下(单位:次/分):44,45,42,48,46,43,47,45.则这组数据的中位数为( )A、48 B、47 C、46 D、456. 如图,将绕点A逆时针旋转一定的度数,得到 . 若点D在线段的延长线上,若则旋转的度数为( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 若正多边形的一个外角的度数为45°,则这个正多边形是( )A、正五边形 B、正六边形 C、正八边形 D、正十边形5. 在九年级体育中考中,某校某班参加仰卧起坐测试的一组女生(每组8人)测试成绩如下(单位:次/分):44,45,42,48,46,43,47,45.则这组数据的中位数为( )A、48 B、47 C、46 D、456. 如图,将绕点A逆时针旋转一定的度数,得到 . 若点D在线段的延长线上,若则旋转的度数为( ) A、 B、 C、 D、7. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A、 B、 C、 D、7. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( ) A、3:4 B、9:16 C、9:1 D、3:18. 下面a , b的取值,能够说明命题“若a>b , 则|a|>|b|”是假命题的是( )A、a=3,b=2 B、a=3,b=-2 C、a=-3,b=-5 D、a=-3,b=59. 如图,已知点 , C是y轴上位于点B上方的一点,平分 , 平分 , 直线交于点D . 若反比例函数()的图像经过点D , 则k的值是( )
A、3:4 B、9:16 C、9:1 D、3:18. 下面a , b的取值,能够说明命题“若a>b , 则|a|>|b|”是假命题的是( )A、a=3,b=2 B、a=3,b=-2 C、a=-3,b=-5 D、a=-3,b=59. 如图,已知点 , C是y轴上位于点B上方的一点,平分 , 平分 , 直线交于点D . 若反比例函数()的图像经过点D , 则k的值是( ) A、-8 B、-9 C、-10 D、-1210. 如图,在中, , D为上一点,以为边,在如图所示位置作正方形 , 点O为正方形的对称中心,且 , 则的长为( )
A、-8 B、-9 C、-10 D、-1210. 如图,在中, , D为上一点,以为边,在如图所示位置作正方形 , 点O为正方形的对称中心,且 , 则的长为( ) A、 B、5 C、5 D、8
A、 B、5 C、5 D、8二、填空题
-
11. 函数 中,自变量 的取值范围是 .12. 2020年4月11日中国向蒙古国紧急援助490000只口罩,表达了中国人民愿同蒙古国携手抗疫、共克时艰的决心和信心.把490000用科学记数法表示为.13. 分解因式: .14. 已知圆锥的母线长为6cm,底面半径为3cm,则此圆锥的侧面积为cm2 .15. 如果 , 那么代数式的值是 .16. 北京冬奥会雪上项目竞赛场地“首钢滑雪大跳台”巧妙地融入了敦煌壁画“飞天”元素.如图,赛道剖面图的一部分可抽象为线段AB . 已知坡AB的长为30m,坡角约为37°,则坡AB的铅直高度AH约为m.(参考数据: , , . )
 17. 抛物线( , 是常数且 , )经过点 . 下列四个结论:①该抛物线一定经过;②;③点 , 在抛物线上,且 , 则④若 , 是方程的两个根,其中 , 则 . 其中正确的结论是(填写序号).18. 在矩形中,点P是矩形边上一点,连接 , 将分别沿翻折,得到 , 当三点共线时,则称P为边上的“优叠点”(如图1).
17. 抛物线( , 是常数且 , )经过点 . 下列四个结论:①该抛物线一定经过;②;③点 , 在抛物线上,且 , 则④若 , 是方程的两个根,其中 , 则 . 其中正确的结论是(填写序号).18. 在矩形中,点P是矩形边上一点,连接 , 将分别沿翻折,得到 , 当三点共线时,则称P为边上的“优叠点”(如图1).
 (1)、若 , 则此时的长度为;(2)、如图2,若将矩形置于平面直角坐标系中, , 点A在原点,B , D分别在x轴与y轴上,点E和点F分别是和边上的动点,运动过程中始终保持 . 当点P是边上唯一的“优叠点”时,连接交于点M , 连接交于点N , 则的最大值为 .
(1)、若 , 则此时的长度为;(2)、如图2,若将矩形置于平面直角坐标系中, , 点A在原点,B , D分别在x轴与y轴上,点E和点F分别是和边上的动点,运动过程中始终保持 . 当点P是边上唯一的“优叠点”时,连接交于点M , 连接交于点N , 则的最大值为 .三、解答题
-
19. 计算:(1)、 ;(2)、 .20.(1)、解方程:(2)、解不等式组:21. 如图,△ABC中,AB=AC , 点E , F在边BC上,BE=CF , 点D在AF的延长线上,AD=AC ,
 (1)、求证:△ABE≌△ACF;(2)、若∠BAE=30°,则∠ADC=°.22. 为了解某区九年级学生身体素质情况,该区从全区九年级学生中随机抽取了部分学生进行了一次体育考试科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)、求证:△ABE≌△ACF;(2)、若∠BAE=30°,则∠ADC=°.22. 为了解某区九年级学生身体素质情况,该区从全区九年级学生中随机抽取了部分学生进行了一次体育考试科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题: (1)、本次抽样测试的学生人数是 ▲ ;m= ▲ ;并把图2条形统计图补充完整;(2)、图1中的度数是°,(3)、该区九年级有学生4500名,如果全部参加这次体育科目测试,请估计不及格的人数是多少?23. 甲城市有2个景点A , B , 乙城市有3个景点C , D , E , 从中随机选取景点游览,(1)、若选取1个景点,则恰好在甲城市的概率为;(2)、若选取2个景点,求出恰好在同一个城市的概率.(用树状图或列表的方式分析)24. 在中, .
(1)、本次抽样测试的学生人数是 ▲ ;m= ▲ ;并把图2条形统计图补充完整;(2)、图1中的度数是°,(3)、该区九年级有学生4500名,如果全部参加这次体育科目测试,请估计不及格的人数是多少?23. 甲城市有2个景点A , B , 乙城市有3个景点C , D , E , 从中随机选取景点游览,(1)、若选取1个景点,则恰好在甲城市的概率为;(2)、若选取2个景点,求出恰好在同一个城市的概率.(用树状图或列表的方式分析)24. 在中, . (1)、请在图1中用无刻度的直尺和圆规作图:作直线l , 使l上的各点到两边的距离相等,设直线l与边交于点D , 在上找一点E , 使;(不写作法,保留作图痕迹)(2)、在(1)的条件下,若 , 则的长为 ▲ . (在备用图中分析)25. 如图,为的直径, , 为上不同于 , 的两点,过点作的切线交直线于点 , 直线于点 .
(1)、请在图1中用无刻度的直尺和圆规作图:作直线l , 使l上的各点到两边的距离相等,设直线l与边交于点D , 在上找一点E , 使;(不写作法,保留作图痕迹)(2)、在(1)的条件下,若 , 则的长为 ▲ . (在备用图中分析)25. 如图,为的直径, , 为上不同于 , 的两点,过点作的切线交直线于点 , 直线于点 . (1)、求证:;(2)、连接 , 若 , 且 , 求的半径.26. 某商品的进价是每件40元,原售价每件60元.进行不同程度的涨价后,统计了商品调价当天的售价和利润情况,以下是部分数据:
(1)、求证:;(2)、连接 , 若 , 且 , 求的半径.26. 某商品的进价是每件40元,原售价每件60元.进行不同程度的涨价后,统计了商品调价当天的售价和利润情况,以下是部分数据:售价(元/件)
60
61
62
63
…
利润(元)
6000
6090
6160
6210
…
(1)、当售价为每件60元时,当天可售出件;当售价为每件61元时,当天可售出件.(2)、若对该商品原售价每件涨价x元(x为正整数)时当天售出该商品的利润为y元.①用所学过的函数知识直接写出y与x之间满足的函数表达式: ▲ .
②如何定价才能使当天的销售利润不低于6200元?
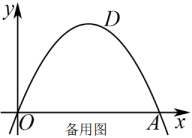
27. 如图,抛物线与x轴交于点 .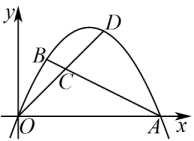
 (1)、求抛物线的函数表达式;(2)、点是抛物线上一点,点C是线段上一点,连接并延长交抛物线于点D , 若 , 求点D的坐标;(3)、抛物线上是否存在点P , 使得?若存在,求出点P的坐标:若不存在,说明理由.28. 如图①,在矩形ABCD中,动点P从点A出发,以1cm/s的速度沿AD向终点D移动,设移动时间为t(s),连接PC , 以PC为一边作正方形PCEF , 连接DE、DF , 设△PCD的面积为y(cm2),y与t之间的函数关系如图②所示.
(1)、求抛物线的函数表达式;(2)、点是抛物线上一点,点C是线段上一点,连接并延长交抛物线于点D , 若 , 求点D的坐标;(3)、抛物线上是否存在点P , 使得?若存在,求出点P的坐标:若不存在,说明理由.28. 如图①,在矩形ABCD中,动点P从点A出发,以1cm/s的速度沿AD向终点D移动,设移动时间为t(s),连接PC , 以PC为一边作正方形PCEF , 连接DE、DF , 设△PCD的面积为y(cm2),y与t之间的函数关系如图②所示.
 (1)、AB=cm , AD=cm;(2)、当t为何值时,△DEF的面积最小?请求出这个最小值;(3)、当t为何值时,△DEF为等腰三角形?请简要说明理由.
(1)、AB=cm , AD=cm;(2)、当t为何值时,△DEF的面积最小?请求出这个最小值;(3)、当t为何值时,△DEF为等腰三角形?请简要说明理由.