浙江省杭州市上城区重点中学2022-2023学八年级下学期期中数学试卷
试卷更新日期:2023-07-17 类型:期中考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列与杭州亚运会有关的图案中,中心对称图形是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列二次根式的运算正确的是( )A、 B、 C、 D、3. 下表是某篮球队的年龄分布,对于不同的值,下列关于年龄的数据量不会发生改变的是( )
2. 下列二次根式的运算正确的是( )A、 B、 C、 D、3. 下表是某篮球队的年龄分布,对于不同的值,下列关于年龄的数据量不会发生改变的是( )年龄岁
频数
A、平均数、中位数 B、中位数、众数 C、中位数、方差 D、平均数、方差4. 用配方法解一元二次方程 , 此方程可化为的正确形式是( )A、 B、 C、 D、5. 若用反证法证明命题“四边形中至少有一个角是钝角或直角”时,则首先应该假设这个四边形中( )A、 至少有一个角是钝角或直角 B、没有一个角是锐角 C、每一个角都是钝角或直角 D、每一个角是锐角6. 一个多边形的内角和是其外角和的倍,则这个多边形是( )A、 七边形 B、八边形 C、九边形 D、十边形7. 如图,在平行四边形ABCD,O是AC、BD的交点,过点O与AC垂直的直线交边AD于点E,若△CDE的周长为11cm,则平行四边形ABCD的周长为( ) A、20cm B、22cm C、24cm D、26cm8. 用长的铁丝围成一个一边靠墙的长方形场地,使该场地的面积为 , 并且在垂直于墙的一边开一个长的小门用其它材料 , 若设垂直于墙的一边长为 , 那么可列方程为( )
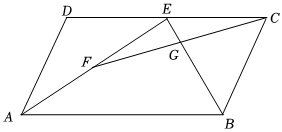
A、20cm B、22cm C、24cm D、26cm8. 用长的铁丝围成一个一边靠墙的长方形场地,使该场地的面积为 , 并且在垂直于墙的一边开一个长的小门用其它材料 , 若设垂直于墙的一边长为 , 那么可列方程为( ) A、 B、 C、 D、9. 如图,在▱中,为边延长线上一点,连结、若 , , 的面积为 , 则的面积为( )
A、 B、 C、 D、9. 如图,在▱中,为边延长线上一点,连结、若 , , 的面积为 , 则的面积为( ) A、 B、 C、 D、10. 对于一元二次方程 , 下列说法:
A、 B、 C、 D、10. 对于一元二次方程 , 下列说法:若 , 则;
若方程有两个不相等的实根,则方程必有两个不相等的实根;
若是方程的一个根,则一定有成立;
若是一元二次方程的根,则;
其中正确的( )
A、 只有 B、只有 C、只有 D、只有二、填空题(本大题共6小题,共24.0分)
-
11. 代数式有意义,则的取值范围是 .12. 超市把元千克的软糖千克,元千克的水果糖千克,混合在一起,则混合后糖果的平均价格为元千克.13. 关于的一元二次方程的两个根分别是与 , 则 .14. 如图,在▱中, , 的平分线交于点 , 连接若 , 则的度数为 .
 15. 如图,水库大坝截面的迎水坡的坡比与的长度之比为: , 背水坡坡比为: , 大坝高 , 坝顶宽 , 则大坝横截面的周长为
15. 如图,水库大坝截面的迎水坡的坡比与的长度之比为: , 背水坡坡比为: , 大坝高 , 坝顶宽 , 则大坝横截面的周长为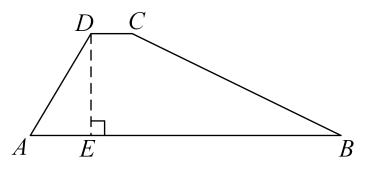 16. 如图,在平行四边形中, , , 将沿翻折至 , 连接当长为 时,是直角三角形.
16. 如图,在平行四边形中, , , 将沿翻折至 , 连接当长为 时,是直角三角形.
三、解答题(本大题共7小题,共66.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 下面是小华同学解答题目的过程:
第一步.
第二步.
第三步.
第四步.
小华的解题过程是否有错误?如果有,请写出正确解答过程.
18. 解方程.(1)、 ;(2)、 .19. 某市举行知识大赛,校、校各派出名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示. (1)、根据图示填写下表:
(1)、根据图示填写下表:平均数/分
中位数/分
众数/分
校
85
校
85
100
(2)、结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;(3)、若校的方差为分 , 计算校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.20. 已知 , .(1)、求的值;(2)、若的小数部分是 , 的整数部分是 , 求的值.21. 某商场一种商品的进价为每件元,售价为每件元每天可销售件,为尽快减少库存,商场决定降价促销.(1)、若该商品连续两次下调相同的百分率后售价降至每件元,求每次降价的百分率;(2)、经调查,若该商品每降价元,每天可多销售件若每天要想获得元的利润且尽快减少库存,每件应降价多少元?