陕西省咸阳市武功县2022-2023学年八年级下学期期中质量调研数学试题

试卷更新日期：2023-07-17 类型：期中考试

进入出卷网下载

一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是符合题意的）

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知 $x < y$ ，则下列结论不成立的是（）

A、 $x - 2 < y - 2$ B、 $3 x + 1 < 3 y + 1$ C、 $- 2 x < - 2 y$ D、 $\frac{x}{3} < \frac{y}{3}$

查看试题解析
3. 用反证法证明“若 $a < | a |$ ，则a为负数”应先假设（）

A、a为正数 B、a为非负数 C、a为负数 D、a为整数

查看试题解析
4. 如图， $B E = C F$ ， $A E ⊥ B C$ 于点E ， $D F ⊥ B C$ 于点F ，要根据“HL”证明 $Rt △ A B E ≌ Rt △ D C F$ ，则还需要添加一个条件是（）

A、 $A E = D F$ B、 $∠ A = ∠ D$ C、 $A B = D C$ D、 $∠ B = ∠ C$

查看试题解析
5. 如图，在 $△ A B C$ 中，已知点D在BC上，且 $B D + A D = B C$ ，则点D在（）

A、AC的垂直平分线上 B、 $∠ B A C$ 的平分线上 C、AB的垂直平分线上 D、BC的中点

查看试题解析
6. 如图，下列条件不能推出 $△ A B C$ 是等腰三角形的是（）

A、 $∠ B = ∠ C$ B、 $A D ⊥ B C$ ， $∠ B A D = ∠ C A D$ C、 $A D ⊥ B C$ ， $B D = C D$ D、 $A D ⊥ B C$ ， $∠ B A D = ∠ A C D$

查看试题解析
7. 若关于x的不等式组 ${\begin{array}{l} x + 6 < 2 + 3 x ， \\ \frac{a + x}{4} > x \end{array}$ 有且只有三个整数解，则实数a的取值范围是（）

A、 $15 \leq a \leq 18$ B、 $15 \leq a < 18$ C、 $5 < a \leq 6$ D、 $15 < a \leq 18$

查看试题解析
8. 如图，在 $Rt △ A B C$ 中， $A C = B C$ ，点D为AB中点， $∠ G D H = 90 °$ ， $∠ G D H$ 绕点D旋转，DG，DH分别与边AC、BC交于E、F两点．下列结论：① $C E = B F$ ， ② $A E + B F = \frac{\sqrt{2}}{2} A B$ ， ③ $S_{四边形 C E D F} = \frac{1}{2} S_{△ A B C}$ ， ④ $△ D E F$ 始终为等腰直角三角形．其中正确的结论有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题（共5小题，每小题3分，计15分）

9. 命题“全等三角形的对应边相等”的逆命题是．

查看试题解析
10. 若关于x的不等式 $a x > 2$ 可化为 $x < \frac{2}{a}$ ，则a的取值范围是．

查看试题解析
11. 如图，在平面直角坐标系中，线段AB端点坐标分别为 $A (- 5 ， 0)$ ， $B (0 ， - 3)$ ，若将线段AB平移至线段 $A_{1} B_{1}$ ，且 $A_{1} (- 3 ， m)$ ， $B_{1} (2 ， 1)$ ，则m的值为．

查看试题解析
12. 如图，已知一次函数 $y_{1} = 3 x + b$ 和 $y_{2} = a x - 3$ 的图象交于点 $P (- 2 ， - 5)$ ，则关于x的不等式 $3 x + b > a x - 3$ 的解集为．

查看试题解析
13. 如图，在四边形ABCD中， $∠ D A B = 30 °$ ，连接AC ，将 $△ A B C$ 绕点B逆时针旋转60°，点C的对应点与点D重合，得到 $△ E B D$ ，若 $A B = 5$ ， $A D = 4$ ，则AC的长度为．

查看试题解析

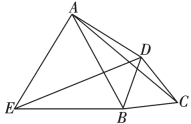
三、解答题（共13小题，计81分．解答应写出过程）

14. 解不等式： $\frac{x - 4}{2} - \frac{x - 1}{4} < 1$ ．

查看试题解析
15. 如图， $△ A B C$ 沿直线l向右平移3 cm，得到 $△ F D E$ ，且 $B C = 6$ cm， $∠ A B C = 45 °$ ．

(1)、求BE的长．

(2)、求 $∠ F D B$ 的度数．

查看试题解析
16. 如图，O是等边 $△ A B C$ 内一点， $∠ O C B = ∠ A B O$ ，求 $∠ B O C$ 的度数．

查看试题解析
17. 如图，已知线段a ， h ．请用尺规作图法作 $△ A B C$ ，使 $A B = A C$ ， $B C = a$ ， BC边上的高 $A D = h$ ．（不写作法，保留作图痕迹）

查看试题解析
18. 解不等式组： ${\begin{array}{l} 1 - 3 (x - 1) < 8 - x ， \\ \frac{x - 3}{2} + 3 \geq x + 1 \end{array}$ 并把解集在如图所示的数轴上表示出来．

查看试题解析
19. 如图，已知 $A N ⊥ O B$ ， $B M ⊥ O A$ ，垂足分别为N、M ， $O M = O N$ ， BM与AN相交于点P ，连接OP ．求证：点P在 $∠ A O B$ 的平分线上．

查看试题解析
20. 如图，在 $△ A B C$ 中，P是BC边上的一点，过点P作BC的垂线，交AB于点Q ，交CA的延长线于点R ．若 $A Q = A R$ ，求证： $△ A B C$ 是等腰三角形．

查看试题解析
21. 如图，AD与BC相交于点O，OA=OC，∠A=∠C，BE=DE．求证：OE垂直平分BD．

查看试题解析
22. 某运输公司要将300吨的货物运往某地，现有A ， B两种型号的汽车可调用，已知A型汽车每辆可装货物20吨，B型汽车每辆可装货物15吨．在每辆汽车不超载的情况下，要把这300吨货物一次性装运完成，并且A型汽车确定要用7辆，至少调用B型汽车多少辆？

查看试题解析
23. 在平面直角坐标系中， $△ A B C$ 的位置如图所示．

（ 1 ）将 $△ A B C$ 沿x轴方向向左平移6个单位，画出平移后得到的 $△ A_{1} B_{1} C_{1}$ ；

（ 2 ）将 $△ A B C$ 绕着点A顺时针旋转90°，画出旋转后得到的 $△ A_{2} B_{2} C_{2}$ ；

（ 3 ）作出 $△ A B C$ 关于原点O成中心对称的 $△ A_{3} B_{3} C_{3}$ ．

查看试题解析
24. 如图，已知 $△ A B C$ 是等边三角形，D是边AC的中点，连接BD ， $E C ⊥ B C$ 于点C ， $C E = B D$ ，连接AE、DE ．求证： $△ A D E$ 是等边三角形．

查看试题解析
25. 某学校计划购买若干台电脑，现从甲、乙两家商场了解到同一型号电脑每台报价均为6000元，并且多买都有一定的优惠．甲商场的优惠条件是：第一台按原价收款，其余每台优惠25%；乙商场的优惠条件是：每台优惠20%．

(1)、试写出甲、乙两商场的收费y（元）与所买电脑台数x之间的关系式；

(2)、若学校只在一家商场购买，选择哪家商场购买更优惠？请说明理由．

查看试题解析
26. 在 $△ A B C$ 中 $A B = A C$ ，点P在平面内，连接AP并将线段AP绕点A顺时针方向旋转与 $∠ B A C$ 相等的角度，得到线段AQ ，连接BQ ．

(1)、【发现问题】如图27，如果点P是BC边上任意一点，则线段BQ和线段PC的数量关系是；

(2)、【探究猜想】如图28，如果点P为平面内任意一点，前面发现的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由，请仅以图2所示的位置关系加以证明（或说明）；

(3)、[拓展应用]如图3，在 $△ A B C$ 中， $A C = 2$ ， $∠ A C B = 90 °$ ， $∠ A B C = 30 °$ ， P是线段BC上的任意一点连接AP ，将线段AP绕点A顺时针方向旋转60°，得到线段AQ ，连接CQ ，请求出线段CQ长度的最小值．

查看试题解析