重庆市梁平区梁山集团2022-2023学年八年级下学期数学期中考试试卷

试卷更新日期：2023-07-17 类型：期中考试

进入出卷网下载

一、单选题

1. 下列二次根式中，属于最简二次根式的是（　　）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{0.8}$ C、 $\sqrt{4}$ D、 $\sqrt{5}$

查看试题解析
2. 使二次根式 $\sqrt{x + 3}$ 有意义的x的取值范围是（）

A、 $x ＞ 3$ B、 $x ＞ - 3$ C、 $x \geq - 3$ D、 $x ≥ 3$

查看试题解析
3. 下列各组数中，以a，b，c为边的三角形不是直角三角形的是（　　）

A、a=1.5，b=2，c=3 B、a=7，b=24，c=25 C、a=6，b=8，c=10 D、a=3，b=4，c=5

查看试题解析
4. 如图所示，在数轴上点A所表示的数为a，则a的值为（）

A、﹣1﹣ $\sqrt{5}$ B、1﹣ $\sqrt{5}$ C、﹣ $\sqrt{5}$ D、﹣1+ $\sqrt{5}$

查看试题解析
5.
如图，长为8cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3cm至D点，则橡皮筋被拉长了（　　）

A、2cm B、3cm C、4cm D、5cm

查看试题解析
6. 如图，平行四边形ABCD中，AD＝5，AB＝3，AE平分∠BAD交BC边于点E，则EC等于（）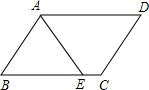

A、1 B、2 C、3 D、4

查看试题解析
7.
如图，正方形ABCD中，AE＝AB，直线DE交BC于点F，则∠BEF＝（）

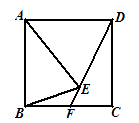A、45° B、30° C、60° D、55°

查看试题解析
8. 如图所示，DE为△ABC的中位线，点F在DE上，且∠AFB=90°，若AB=6，BC=10，则EF的长为（）

A、1 B、2 C、3 D、5

查看试题解析
9. 如图，在矩形ABCD中，AB＝8，BC＝4，将矩形沿AC折叠，点D落在D′处，则重叠部分 $△$ AFC的面积是（）

A、8 B、10 C、20 D、32

查看试题解析
10. 如图，点O为正方形ABCD的中心，BE平分∠DBC交DC于点E，延长BC到点F，使FC=EC，连结DF交BE的延长线于点H，连结OH交DC于点G，连结HC．则以下四个结论中：①OH∥BF，②GH= $\frac{1}{4}$ BC，③OD= $\frac{1}{2}$ BF，④∠CHF=45°．正确结论的个数为（）

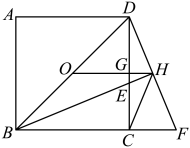A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 计算： $（ \sqrt{3} ）^{2} =$ ； $\sqrt{20} =$ ．

查看试题解析
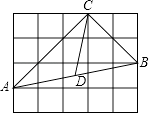
12. 已知 $x = \frac{\sqrt{5} - 2}{2}$ ，则 $x^{2} + x + 1 =$ ．

查看试题解析
13. 当x=时，二次根式 $\sqrt{x + 1}$ 取最小值，其最小值为．

查看试题解析
14. 如图，每个小正方形的边长为1，在△ABC中，点D为AB的中点，则线段CD的长为．

查看试题解析
15. 勾股定理是人类早期发现并证明的重要数学定理之一，是用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一．它不但因证明方法层出不穷吸引着人们，更因为应用广泛而使人入迷．如图，秋千静止时，踏板离地的垂直高度 $B E = 1 m$ ，将它往前推 $6 m$ 至 $C$ 处时（即水平距离 $C D = 6 m$ ），踏板离地的垂直高度 $C F = 4 m$ ，它的绳索始终拉直，则绳索 $A C$ 的长是 $m$ ．

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ B A C = 90 ° ， A B = 3 ， A C = 4 ， B C = 5$ ， $E F$ 垂直平分 $B C$ ，点P为直线 $E F$ 上的任一点，则 $A P + B P$ 的最小值是．

查看试题解析
17. 如图，E、F分别是矩形ABCD的边AD、AB上的点，若EF=EC，EF⊥EC，DC= $\sqrt{2}$ ，则BE的长为__．

查看试题解析
18. 如图，在边长为6的正方形 $A B C D$ 中，E是边 $C D$ 的中点，F在 $B C$ 边上，且 $∠ E A F = 45 °$ ，连接 $E F$ ，则 $B F$ 的长为．

查看试题解析

三、解答题

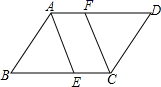
19. 计算及解方程组：

(1)、 $\sqrt{3} \div （ \sqrt{24} - 2 \sqrt{\frac{1}{6}} ） - | 1 - \sqrt{2} |$

(2)、 $\sqrt{6} (2 \sqrt{2} - \sqrt{15}) + {(\sqrt{3} - 2)}^{2}$

查看试题解析
20. 先化简，再求值： $(1 + \frac{3}{a - 1}) \div \frac{a^{2} + 4 a + 4}{2 a - 2}$ ，其中 $a = \sqrt{2} - 2$ ．

查看试题解析
21. 如图，已知▱ABCD中，AE平分∠BAD ， CF平分∠BCD ，分别交BC、AD于E、F ．求证：DF=BE ．

查看试题解析
22. 已知：如图，四边形ABCD中，AB⊥BC，AB＝2，BC＝4，CD＝4，AD＝6，求四边形ABCD的面积．

查看试题解析
23. 如图，在Rt△ABC中，∠B＝90°，AC＝60 cm，∠A＝60°，点D从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是t秒(0＜t≤15)．过点D作DF⊥BC于点F，连结DE，EF.

(1)、四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；

(2)、当t为何值时，△DEF为直角三角形？请说明理由．

查看试题解析
24. 如图，在矩形 $A B C D$ 中，E、F分别是边 $A B 、 C D$ 上的点， $A E = C F$ ，连接 $E F 、 B F$ ， $E F$ 与对角线 $A C$ 交于点O，且 $B E = B F$ ， $∠ B E F = 2 ∠ B A C$ ．若 $B C = 2 \sqrt{3}$ ，求 $A B$ 的长．

查看试题解析
25. 阅读材料：
小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如 $3 + 2 \sqrt{2} = (1 + \sqrt{2})^{2}$ ．善于思考的小明进行了以下探索：

设 $a + b \sqrt{2} = (m + n \sqrt{2})^{2}$ （其中a、b、m、n均为整数），则有 $a + b \sqrt{2} = m^{2} + 2 n^{2} + 2 m n \sqrt{2}$ ．

$∴ a = m^{2} + 2 n^{2}$ ， $b = 2 m n$ ．这样小明就找到了一种把类似 $a + b \sqrt{2}$ 的式子化为平方式的方法．

请你仿照小明的方法探索并解决下列问题：

(1)、当a、b、m、n均为正整数时，若 $a + b \sqrt{3} = (m + n \sqrt{3})^{2}$ ，用含m、n的式子分别表示a、b，得： $a =$ ， $b =$ ；

(2)、利用所探索的结论，找一组正整数a、b、m、n填空：+ $\sqrt{3}$ =（+ $\sqrt{3})^{2}$ ；

(3)、若 $a + 4 \sqrt{3} = (m + n \sqrt{3})^{2}$ ，且a、m、n均为正整数，求a的值？

(4)、化简： $\sqrt{6 + 2 \sqrt{5}}$ ．

查看试题解析
26. 如图，在边长为4的正方形ABCD中，点P在AB上从A向B运动，连接DP交AC于点Q．

(1)、试证明：无论点P运动到AB上何处时，都有△ADQ≌△ABQ；

(2)、当△ABQ的面积是正方形ABCD面积的 $\frac{1}{6}$ 时，求DQ的长；

(3)、若点P从点A运动到点B，再继续在BC上运动到点C，在整个运动过程中，当点P运动到什么位置时，△ADQ恰为等腰三角形．

查看试题解析