湖南省常德市安乡县2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-17 类型:期中考试
一、单选题
-
1. 以下列各组数据为边长作三角形,其中不能组成直角三角形的是( )A、4,6,8 B、5,12,13 C、6,8,10 D、7,24,252. 如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得 . 据此,可求得学校与工厂之间的距离等于( )
 A、 B、 C、3.5km D、3. 下列图形中,是中心对称图形的是( )A、
A、 B、 C、3.5km D、3. 下列图形中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 一个多边形的内角和为360°,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形5. 矩形具有而平行四边形不一定具有的性质是( )A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分6. 如图,在矩形中,平分交于点E,连接 , 若 , 则的长为( )
4. 一个多边形的内角和为360°,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形5. 矩形具有而平行四边形不一定具有的性质是( )A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分6. 如图,在矩形中,平分交于点E,连接 , 若 , 则的长为( ) A、12 B、14 C、16 D、207. 如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )
A、12 B、14 C、16 D、207. 如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )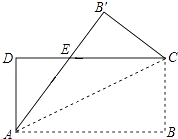 A、∠DAB′=∠CAB′ B、∠ACD=∠B′CD C、AD=AE D、AE=CE8. 如图以a、b、c为边作一个 , 其中 , 分别以各边为边向外作三个正方形、正方形、正方形 , 面积分别为S、、 , 其中B、C、H在同一直线上, A、C、G三点在同一条直线上,连接、 , 过C作 , 垂足为K,交于M,嘉淇在用本图证明勾股定理时,下列结论不成立的是( )
A、∠DAB′=∠CAB′ B、∠ACD=∠B′CD C、AD=AE D、AE=CE8. 如图以a、b、c为边作一个 , 其中 , 分别以各边为边向外作三个正方形、正方形、正方形 , 面积分别为S、、 , 其中B、C、H在同一直线上, A、C、G三点在同一条直线上,连接、 , 过C作 , 垂足为K,交于M,嘉淇在用本图证明勾股定理时,下列结论不成立的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 已知直角三角形的一个锐角为36°,则另一个锐角的大小为.10. 如图,九洞天风景区内的路互相垂直,路的中点与点被经过景区的六冲河隔开.若测得路的长为 , 则、两点间的距离 .
 11. 如图,是边长为的等边三角形,将沿直线平移至的位置,连接 , 则的长是 .
11. 如图,是边长为的等边三角形,将沿直线平移至的位置,连接 , 则的长是 . 12. 如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件 .
12. 如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件 . 13. 一个正多边形的内角和为 , 则这个正多边形的每一个外角等于度.14. 如图所示,在中, , 是斜边的中线,于点E,若 , , 则的面积为 .
13. 一个正多边形的内角和为 , 则这个正多边形的每一个外角等于度.14. 如图所示,在中, , 是斜边的中线,于点E,若 , , 则的面积为 . 15. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=20°,则∠B= .
15. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=20°,则∠B= . 16. 如图,将四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”.设直角三角形较长直角边长为x,较短直角边长为y.已知 , 大正方形边长为5,则小正方形的面积为 .
16. 如图,将四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”.设直角三角形较长直角边长为x,较短直角边长为y.已知 , 大正方形边长为5,则小正方形的面积为 .
三、解答题
-
17. 如图,是等边三角形,点、、分别是、、的中点,求证:是等边三角形.
 18. 如图, , 分别是平行四边形的边 , 上的点,已知 . 求证: .
18. 如图, , 分别是平行四边形的边 , 上的点,已知 . 求证: . 19. 如图,在中, , 高、交于点O,求的度数.
19. 如图,在中, , 高、交于点O,求的度数. 20. 如图,一架梯子长13米,斜靠在一面墙上,梯子底端离墙5米.
20. 如图,一架梯子长13米,斜靠在一面墙上,梯子底端离墙5米. (1)、这个梯子的顶端距地面有多高?(2)、如果梯子的顶端下滑了5米,那么梯子的底端在水平方向滑动了多少米?21. 如图,在涪江笔直的河流一侧有一旅游地C,河边有两个景点A、B.其中 , 因C到A的路不通,为方便游客决定在河边新建一个景点H(A、H、B三点在同一直线上),并新修一条路CH,测得千米,千米,千米.
(1)、这个梯子的顶端距地面有多高?(2)、如果梯子的顶端下滑了5米,那么梯子的底端在水平方向滑动了多少米?21. 如图,在涪江笔直的河流一侧有一旅游地C,河边有两个景点A、B.其中 , 因C到A的路不通,为方便游客决定在河边新建一个景点H(A、H、B三点在同一直线上),并新修一条路CH,测得千米,千米,千米. (1)、判断△BCH的形状,并说明理由;(2)、求原路线AC的长.22. 如图,在中,D、E分别为AB、AC的中点,过点C作交DE的延长线于点F.
(1)、判断△BCH的形状,并说明理由;(2)、求原路线AC的长.22. 如图,在中,D、E分别为AB、AC的中点,过点C作交DE的延长线于点F. (1)、求证:四边形BCFD为平行四边形;(2)、若 , 求EF的长.23. 如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD的延长线于点F,连接CF.
(1)、求证:四边形BCFD为平行四边形;(2)、若 , 求EF的长.23. 如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD的延长线于点F,连接CF.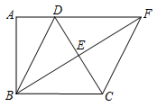 (1)、求证:四边形BCFD是菱形;(2)、若AD=1,BC=2,求BF的长.24. 如图,四边形ABCD中,∠BAD=90°,∠DCB=90°,EF分别是BD、AC的中点,
(1)、求证:四边形BCFD是菱形;(2)、若AD=1,BC=2,求BF的长.24. 如图,四边形ABCD中,∠BAD=90°,∠DCB=90°,EF分别是BD、AC的中点, (1)、请你猜测EF与AC的位置关系,并给予证明;(2)、当AC=8,BD=10时,求EF的长.25. 【阅读】
(1)、请你猜测EF与AC的位置关系,并给予证明;(2)、当AC=8,BD=10时,求EF的长.25. 【阅读】定义:如果一个三角形有两个内角的差为90°,那么这样的三角形叫做“准直角三角形”.
(1)、【理解】①若 , , 则“准直角三角形”;(填“是”或“不是”)
②已知是“准直角三角形”,且 , , 则的度数为 .
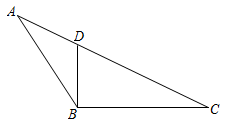
(2)、【应用】如图,在中,点D在上,连接 . 若 , , , , 试说明是“准直角三角形”.
 26. 如图1,是平行四边形对角线的交点,过点作 , , 垂足分别为 , , 若 , 我们称是平行四边形的心距比.
26. 如图1,是平行四边形对角线的交点,过点作 , , 垂足分别为 , , 若 , 我们称是平行四边形的心距比.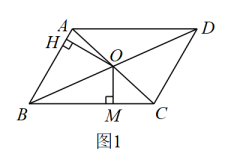 (1)、如图2,四边形是矩形, , , 则 .
(1)、如图2,四边形是矩形, , , 则 . (2)、如图3,四边形是平行四边形, , 求证:四边形是菱形.
(2)、如图3,四边形是平行四边形, , 求证:四边形是菱形. (3)、已知如图,在中, , 点、、分别在、、边上,若存在一个四边形是平行四边形,且 , 请通过尺规作图作出一个点 . (不写作法,但保留作图痕迹;如若有必要,可简述作图思路)
(3)、已知如图,在中, , 点、、分别在、、边上,若存在一个四边形是平行四边形,且 , 请通过尺规作图作出一个点 . (不写作法,但保留作图痕迹;如若有必要,可简述作图思路)