湖南省邵阳市北塔区2022--2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-17 类型:期中考试
一、单选题
-
1. 如图,AB∥DF,AC⊥CE于C,BC与DF交于点E,若∠A=20°,则∠CEF等于( )
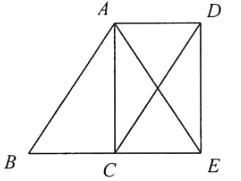
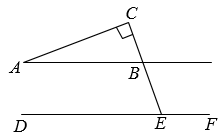 A、110° B、100° C、80° D、70°2. 若一个多边形的外角和是它内角和的 , 那么这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形3. 如图,∠C=∠D=90°,添加下列条件:①AC=AD;②∠ABC=∠ABD;③BC=BD,其中能判定Rt△ABC与Rt△ABD全等的条件有( )
A、110° B、100° C、80° D、70°2. 若一个多边形的外角和是它内角和的 , 那么这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形3. 如图,∠C=∠D=90°,添加下列条件:①AC=AD;②∠ABC=∠ABD;③BC=BD,其中能判定Rt△ABC与Rt△ABD全等的条件有( )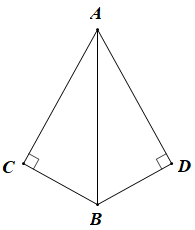 A、0个 B、1个 C、2个 D、3个4. 如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )
A、0个 B、1个 C、2个 D、3个4. 如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )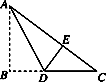 A、6 B、5 C、4 D、35. 平行四边形、矩形、菱形、正方形共有的性质是( )A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、对角线互相垂直平分6. 如图,在平面直角坐标系中,菱形的顶点D在x轴上,边在y轴上,若点A的坐标为 , 则C点的坐标为( )
A、6 B、5 C、4 D、35. 平行四边形、矩形、菱形、正方形共有的性质是( )A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、对角线互相垂直平分6. 如图,在平面直角坐标系中,菱形的顶点D在x轴上,边在y轴上,若点A的坐标为 , 则C点的坐标为( )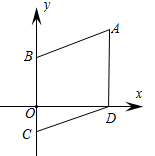 A、 B、 C、 D、7. 如图,在△ABC中,点D、E、F分别是边AB、BC、CA上的中点,且AB=8cm,AC=10cm,则四边形ADEF的周长等于( )cm.
A、 B、 C、 D、7. 如图,在△ABC中,点D、E、F分别是边AB、BC、CA上的中点,且AB=8cm,AC=10cm,则四边形ADEF的周长等于( )cm.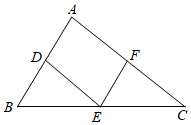 A、14 B、18 C、20 D、248. 若点P(1-m,-3)在第四象限,则m的取值范围是( )A、m<1 B、m<0 C、m>0 D、m>19. 如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB=6,OA=OB=5,则点A的坐标是( )
A、14 B、18 C、20 D、248. 若点P(1-m,-3)在第四象限,则m的取值范围是( )A、m<1 B、m<0 C、m>0 D、m>19. 如图,△OAB的顶点O(0,0),顶点A,B分别在第一、四象限,且AB⊥x轴,若AB=6,OA=OB=5,则点A的坐标是( ) A、 B、 C、 D、10. 下列图形,是中心对称图形的是( )A、
A、 B、 C、 D、10. 下列图形,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
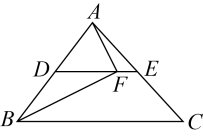
11. 在中, , 若E为的中点,则 .12. 已知点P位于第四象限内,且点P到x轴的距离是2,到y轴的距离是4,则点P的坐标为 .13. 如图所示,为的中位线,点F在上,且 , 若 , , 则的长为 .
 14. 如图, .
14. 如图, .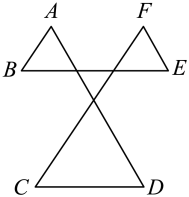 15. 如图,在△ABC中,D,E,F分别是AB,BC和AC边的中点,请添加一个条件 , 使四边形BEFD为矩形.(填一个即可)
15. 如图,在△ABC中,D,E,F分别是AB,BC和AC边的中点,请添加一个条件 , 使四边形BEFD为矩形.(填一个即可)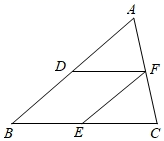 16. 如图,以Rt△ABC的三边为边长分别向外作正方形,若斜边为10,则图中阴影部分的面积 .
16. 如图,以Rt△ABC的三边为边长分别向外作正方形,若斜边为10,则图中阴影部分的面积 .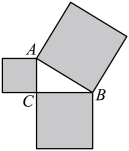 17. 如图,在△ABC中,∠BAC=90°.AD⊥BC于点D,若∠C=30°,BD=1,则线段CD的长为.
17. 如图,在△ABC中,∠BAC=90°.AD⊥BC于点D,若∠C=30°,BD=1,则线段CD的长为.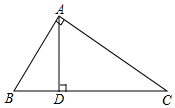 18. 在平面直角坐标系中,点关于轴的对称点为 , 将点向左平移3个单位得到点 , 则的坐标为 .
18. 在平面直角坐标系中,点关于轴的对称点为 , 将点向左平移3个单位得到点 , 则的坐标为 .三、解答题
-
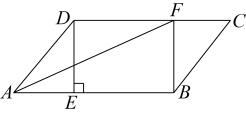
19. 如图,菱形的对角线 , 相交于点 , 为的中点,若 , , 求菱形的面积.
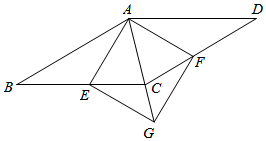
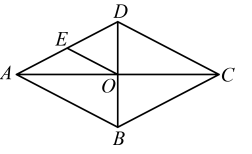 20. 如图,是等腰直角三角形, , 为上一点,延长至点使 , 连接、并延长交于点 . 求证:是直角三角形.
20. 如图,是等腰直角三角形, , 为上一点,延长至点使 , 连接、并延长交于点 . 求证:是直角三角形.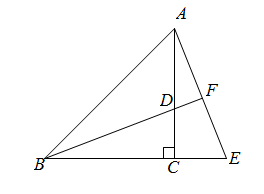 21. 如图,在平行四边形ABCD中,点E,F分别在AB、CD上,AE=CF ,且DF=BF; 求证:四边形DEBF为菱形。
21. 如图,在平行四边形ABCD中,点E,F分别在AB、CD上,AE=CF ,且DF=BF; 求证:四边形DEBF为菱形。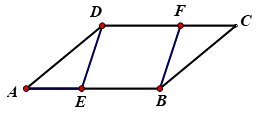 22. 如图, ,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.求证: .
22. 如图, ,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.求证: .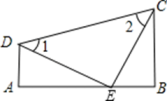 23. 如图,在▱ABCD中,点O是对角线AC、BD的交点,EF过点O且垂直于AD.
23. 如图,在▱ABCD中,点O是对角线AC、BD的交点,EF过点O且垂直于AD.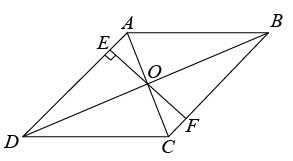 (1)、求证:OE=OF;(2)、若S▱ABCD=63,OE=3.5,求AD的长.
(1)、求证:OE=OF;(2)、若S▱ABCD=63,OE=3.5,求AD的长.