湖南省永州市宁远县2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-17 类型:期中考试
一、单选题
-
1. 五根小棒的长度(单位:)分别为6,7,8,9,10,现从中选择三根,将它们首尾相接摆成三角形,其中能摆成直角三角形的是( )A、6,7,8 B、6,8,10 C、7,8,9 D、7,9,102. 下列命题中,真命题是( )A、面积相等的两个三角形全等 B、如果 , 那么 C、有一个角是的三角形是等边三角形 D、角平分线上的点到角两边的距离相等3. 若一个n边形的内角和为900°,则n的值是( )A、9 B、7 C、6 D、54. 在平行四边形中, , 则( )A、 B、 C、 D、5. 在△ABC中,∠C=90°,AB=3,则AB2+BC2+AC2的值为( )A、6 B、9 C、12 D、186. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、正六边形 B、正五边形 C、平行四边形 D、正三角形7. 下列命题中,①对角线相等且互相平分的四边形是矩形;②对角线互相垂直的四边形是菱形;③四边相等的四边形是正方形;④四边相等的四边形是菱形,是真命题的有( )A、①② B、②④ C、①④ D、①②④8. 下列说法不正确的是( )A、两条直角边对应相等的两个直角三角形全等 B、一锐角和斜边对应相等的两个直角三角形全等 C、斜边和一直角边对应相等的两个直角三角形全等 D、有两边相等的两个直角三角形全等9. 如图,在中, , , 平分 , , 是边上一动点,则 , 之间的最小距离为( )
 A、2 B、3 C、4 D、610. 如图平行四边形中,对角线相交于点 , 点E是的中点,若 , 则的长为( )
A、2 B、3 C、4 D、610. 如图平行四边形中,对角线相交于点 , 点E是的中点,若 , 则的长为( )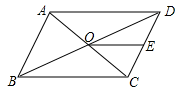 A、3 B、12 C、8 D、10
A、3 B、12 C、8 D、10二、填空题
-
11. 如图,在等边中,是边上的中线,过点D作于点E,且 , 则的长为 .
 12. 如果一个多边形的每个外角都等于 , 则这个多边形的边数为.13. 如图,直线a、b、c分别表示相互交叉的马路,要建一个停车场要求到三条马路的距离相等,那么符合条件的修建点有处.
12. 如果一个多边形的每个外角都等于 , 则这个多边形的边数为.13. 如图,直线a、b、c分别表示相互交叉的马路,要建一个停车场要求到三条马路的距离相等,那么符合条件的修建点有处. 14. 菱形的两条对角线的长分别为6和8,则这个菱形的周长为.15. 在中, , , , 则的长是 .16. 如图,是的中位线,平分 , 交于 , 若 , 则 .
14. 菱形的两条对角线的长分别为6和8,则这个菱形的周长为.15. 在中, , , , 则的长是 .16. 如图,是的中位线,平分 , 交于 , 若 , 则 . 17. 如图,∠A=∠D=90°,AC=DB,则△ABC≌△DCB的理由是
17. 如图,∠A=∠D=90°,AC=DB,则△ABC≌△DCB的理由是 18. 如图,矩形纸片中, , E为上一点,平分 , , 则的长为 .
18. 如图,矩形纸片中, , E为上一点,平分 , , 则的长为 .
三、解答题
-
19. 如图,在四边形中,已知 , , , , .
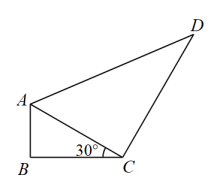 (1)、求证:是直角三角形(2)、求四边形的面积.20. 已知:如图,在平行四边形中, , 是对角线上两点,连接 , , 求证: .
(1)、求证:是直角三角形(2)、求四边形的面积.20. 已知:如图,在平行四边形中, , 是对角线上两点,连接 , , 求证: . 21. 如图,在菱形中,过点B作于点E,点F在边上, , 求证:四边形是矩形.
21. 如图,在菱形中,过点B作于点E,点F在边上, , 求证:四边形是矩形. 22. 某校把一块形状为直角三角形的废地开辟为生物园,如图所示, , , , 线段是一条水渠,且点在边上,已知水渠的造价为元 , 问:当水渠的造价最低时,长为多少米?最低造价是多少元?
22. 某校把一块形状为直角三角形的废地开辟为生物园,如图所示, , , , 线段是一条水渠,且点在边上,已知水渠的造价为元 , 问:当水渠的造价最低时,长为多少米?最低造价是多少元? 23. 如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE、AF.
23. 如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE、AF.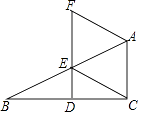 (1)、证明:AF=CE;(2)、当∠B=30°时,试判断四边形ACEF的形状并说明理由.24. 如图,在 中, ,过 的中点D作 , ,垂足分别为点E、F.
(1)、证明:AF=CE;(2)、当∠B=30°时,试判断四边形ACEF的形状并说明理由.24. 如图,在 中, ,过 的中点D作 , ,垂足分别为点E、F.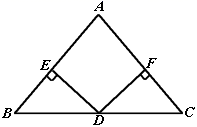 (1)、求证: ;(2)、若 ,求 的度数.
(1)、求证: ;(2)、若 ,求 的度数.