安徽省黄山市2022—2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-07-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图案分别是现代、奔驰、长城、奥迪汽车的车标，其中，可以看作由“基本图案”经过平移得到的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列说法正确的是（　　）

A、 $\sqrt{9}$ 的算术平方根是3 B、0的算术平方根是0 C、 $- 16$ 的平方根是 $- 4$ D、 $0.1$ 的立方根是 $0.001$

查看试题解析
3. 若 $a > b$ ，则下列式子中正确的是（　　）

A、 $1 - a > 1 - b$ B、 $a - 3 < b - 3$ C、 $- 3 a < - 3 b$ D、 $b - a > 0$

查看试题解析
4. 一个正方形的面积为28，则它的边长应在（）

A、3到4之间 B、4到5之间 C、5到6之间 D、6到7之间

查看试题解析
5. 下列调查中，适宜采用全面调查方式的是（　　）

A、对全市每天丢弃的过期药品的调查 B、对冷饮市场上雪糕质量情况的调查 C、对全国中学生心理健康现状的调查 D、对国产大飞机 $C 919$ 各零件部件的调查

查看试题解析
6. 在实数 $\frac{22}{7}$ ， $\sqrt{2}$ ， $π$ ， $3 . \dot{1} \dot{4}$ ， $3.1212212221 \dots$ ， $2 + \sqrt{3}$ 中，无理数的个数有（　　）

A、5个 B、4个 C、3个 D、2个

查看试题解析
7. 如图，在平面直角坐标系中，动点 $P$ 按图中箭头所示方向从原点出发，第1次运动到点 $P_{1} (1 ， 1)$ ，第2次接着运动到点 $P_{2} (2 ， 0)$ ，第3次接着运动到点 $P_{3} (3 ， - 2)$ ，第4次接着运动到点 $P_{4} (4 ， 0) ， \dots$ 按这样的运动规律，点 $P_{2023}$ 的坐标是（　　）

A、 $(2023 ， - 2)$ B、 $(2023 ， 1)$ C、 $(2024 ， 0)$ D、 $(2022 ， 0)$

查看试题解析
8. 如图，已知 $A B$ $∥ D E$ ， $∠ A = 25 °$ ， $∠ C D E = 135 °$ ，则 $∠ A C D$ 的度数是（　　）

A、 $45 °$ B、 $60 °$ C、 $70 °$ D、 $90 °$

查看试题解析
9. 已知方程组 ${\begin{array}{l} 2 x - y = 7 a - 5 \\ 2 y - x = 5 \end{array}$ 的解 $x ， y$ 互为相反数，则a的值为（　　）

A、0 B、1 C、 $- 1$ D、2

查看试题解析
10. 在平面直角坐标系中，下列说法：①若点 $A (a ， b)$ 在坐标轴上，则 $a b = 0$ ；②若 $m$ 为任意实数，则点 $(2 ， m^{2})$ 一定在第一象限；③若点 $P$ 到 $x$ 轴的距离与到 $y$ 轴距离均为 $2$ ，则符合条件的点 $P$ 有 $2$ 个；④已知点 $M (2 ， 3)$ ，点 $N (- 2 ， 3)$ ，则 $M N ∥ x$ 轴．其中正确的是（　　）

A、①④ B、②③ C、①③④ D、①②③④

查看试题解析

二、填空题

11. 若 $\frac{1}{2} x^{2} y^{7 - m}$ 与 $x^{n - 1} y$ 是同类项，则 $m + n$ 的平方根是．

查看试题解析
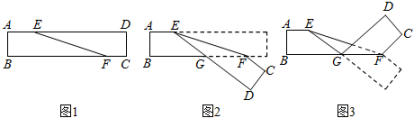
12. 把命题“对顶角相等”改写成“如果……，那么……”的形式为．

查看试题解析
13. 已知点 $A (3 x - 6 ， 4 y + 15)$ ，点 $B (5 y ， x)$ 关于x轴对称，则 $x + y$ 的值是．

查看试题解析
14. 折叠问题的实质是图形的轴对称变换，所以在解决折叠问题时可以充分运用轴对称的思想和轴对称的性质．如图1， $∠ D E F = 25 °$ ，将长方形纸片 $A B C D$ 沿直线 $E F$ 折叠成图2，再沿直线 $G F$ 折叠成图3，则图3中 $∠ C F E =$ ．

查看试题解析
15. 数轴上点 $A$ 表示的数为 $- \sqrt{2}$ ，将点 $A$ 沿数轴向右平移 $2$ 个单位长度到达点 $B$ ，设点 $B$ 所表示的数为 $m$ ，则 $| m - 1 | - | 2 - m | =$ ．

查看试题解析
16. 已知 $\sqrt[3]{2 x + 1}$ -2x-1＝0，则x＝．

查看试题解析
17. 在同一平面内， $∠ A$ 与 $∠ B$ 的两边一边平行，另一边垂直，且 $∠ A$ 比 $∠ B$ 的3倍少10°.则 $∠ B$ .

查看试题解析
18. 如果关于x的不等式组 ${\begin{array}{l} 1 - \frac{3 x + 2}{2} \leq 4 \\ x < m \end{array}$ 恰有4个整数解，则m的取值范围是．

查看试题解析

三、解答题

19. 计算 $\sqrt[3]{8} - | - \sqrt[3]{8} | - (\sqrt{3} - \sqrt{5}) - | \sqrt{5} - 2 |$

查看试题解析
20. 解不等式 $1 - \frac{x - 2}{2} \geq \frac{1 + x}{3}$ ，并写出它的非负整数解.

查看试题解析
21. 如图，在由边长为1个单位长度的正方形组成的网格中，用 $(- 1 ， 0)$ 表示A点的位置，用 $(3 ， 1)$ 表示 $B$ 点的位置．

(1)、请画出平面直角坐标系并写出 $C$ 点的坐标．

(2)、请画出△ $C D E$ 向下平移1个单位长度，再向右平移3个单位长度后的 $△ C_{1} D_{1} E_{1}$ ．

(3)、求△ $C_{1} D_{1} E_{1}$ 的面积．

查看试题解析
22. 我市为营造良好的读书育人氛围，为学生未来发展奠定坚实基础，决定从2022年秋季开始，在全市教育系统实施“悦读黄山·书香徽州”阅读行动．某校想了解学生每周的课外阅读时间情况，随机调查了部分学生，对学生每周的课外阅读时间 $x$ 小时进行分组整理，并绘制了不完整的频数分布直方图和扇形统计图（如图），根据图中提供的信息，解答下列问题：

(1)、这次抽样调查的学生人数是人；

(2)、扇形统计图中“D”组对应的圆心角度数为，并将条形统计图补充完整；

(3)、若该校有1500名学生，估计全校有多少名学生每周的课外阅读时间不少于4小时？

查看试题解析
23. 著名数学教育家G•波利亚，有句名言：“发现问题比解决问题更重要”．这句话启发我们：要想学会数学，就需要观察，发现问题，探索问题的规律性东西，要有一双敏锐的眼睛．请先观察下列等式找出规律，并解答问题．
① $1^{3} = 1^{2}$ ；

② $1^{3} + 2^{3} = 3^{2}$ ；

③ $1^{3} + 2^{3} + 3^{3} = 6^{2}$ ；

④ $1^{3} + 2^{3} + 3^{3} + 4^{3} = 1 0^{2}$ ；

⑤ $1^{3} + 2^{3} + 3^{3} + 4^{3} + 5^{3} = 1 5^{2}$

……………

(1)、等式⑥是．

(2)、 $1^{3} + 2^{3} + 3^{3} + … + n^{3} =$ （n为正整数）．

(3)、求 $1 1^{3} + 1 2^{3} + 1 3^{3} + 1 4^{3} + 1 5^{3}$ 的值．

查看试题解析
24. 为降低空气污染，公交公司决定全部更换节能环保的燃气公交车，计划购买A型和B型两种公交车，其中每台的价格，年载客量如表：

A型
B型
价格（万元/台）
a
b
年载客量（万人/年）
60
100
若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元．

(1)、求a，b的值；

(2)、计划购买A型和B型两种公交车共10辆，如果该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次．请你设计一个方案，使得购车总费用最少．

查看试题解析
25. 综合与实践
学习了相交线、平行线相关知识后，某数学兴趣小组利用手中的一副三角板进行了探究，发现和提出了一些数学问题．如图1所示，他们将两个直角三角板的两个直角顶点 $C$ 叠放在一起，其中 $∠ A = 30 °$ ， $∠ B = 60 °$ ， $∠ D = ∠ E = 45 °$ ．

(1)、猜想 $∠ B C D$ 与 $∠ A C E$ 的数量关系，并说明理由；

(2)、若 $∠ B C D = 3 ∠ A C E$ ，求 $∠ B C D$ 的度数；

(3)、若按住三角板 $A B C$ 不动，绕顶点 $C$ 转动三角板 $D C E$ ，试探究 $∠ B C D$ 等于多少度时 $C E ∥ A B$ ，简要说明理由．

查看试题解析

	A型	B型
价格（万元/台）	a	b
年载客量（万人/年）	60	100