贵州省遵义市2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-17 类型:期末考试
一、单选题
-
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、2. 下面四个手机应用图标中是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 3. 下列各组数中,是勾股数的是( )A、6,8,12 B、 , 1 C、8,15,16 D、9,12,154. 在中,若 , 下列图形中最符合条件的图形是( )A、
3. 下列各组数中,是勾股数的是( )A、6,8,12 B、 , 1 C、8,15,16 D、9,12,154. 在中,若 , 下列图形中最符合条件的图形是( )A、 B、
B、 C、
C、 D、
D、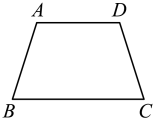 5. 共同富裕的要求是:在消除两极分化和贫穷基础上实现普遍富裕.下列有关个人收入的统计量中,最能体现共同富裕要求的是( )A、平均数小,方差大 B、平均数小,方差小 C、平均数大,方差小 D、平均数大,方差大6. 下列计算正确的是( )A、 B、=4 C、()2=6 D、=27. 如图,四边形ABCD是平行四边形,以点A为圆心,AB的长为半径画弧,交AD于点F;分别以点B,F为圆心,大于的长为半径画弧,两弧相交于点G:连接AG并延长,交BC于点E.连接BF,若 , , 则AB的长为( )
5. 共同富裕的要求是:在消除两极分化和贫穷基础上实现普遍富裕.下列有关个人收入的统计量中,最能体现共同富裕要求的是( )A、平均数小,方差大 B、平均数小,方差小 C、平均数大,方差小 D、平均数大,方差大6. 下列计算正确的是( )A、 B、=4 C、()2=6 D、=27. 如图,四边形ABCD是平行四边形,以点A为圆心,AB的长为半径画弧,交AD于点F;分别以点B,F为圆心,大于的长为半径画弧,两弧相交于点G:连接AG并延长,交BC于点E.连接BF,若 , , 则AB的长为( )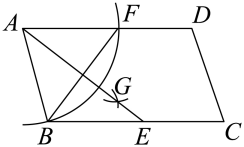 A、3 B、4 C、5 D、88. 已知 , , , 中有三个点在同一直线上,不在此直线上的点是( )A、点 B、点 C、点 D、点9. 如图,在方格中作以为一边的 , 要求点也在格点上,这样的能作出( )
A、3 B、4 C、5 D、88. 已知 , , , 中有三个点在同一直线上,不在此直线上的点是( )A、点 B、点 C、点 D、点9. 如图,在方格中作以为一边的 , 要求点也在格点上,这样的能作出( )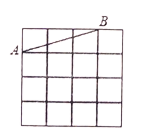 A、个 B、个 C、 个 D、个10. 如图,已知在矩形中,对角线 , 相交于点O,于点E.若 , 则的度数是( )
A、个 B、个 C、 个 D、个10. 如图,已知在矩形中,对角线 , 相交于点O,于点E.若 , 则的度数是( ) A、 B、 C、 D、11. 如图,:和:相交于 , 则解集为( )
A、 B、 C、 D、11. 如图,:和:相交于 , 则解集为( )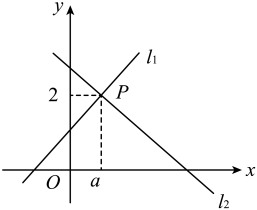 A、 B、 C、 D、12. 如图,在平行四边形中, , 于E,于F,交于H,、的延长线交于E,给出下列结论:
A、 B、 C、 D、12. 如图,在平行四边形中, , 于E,于F,交于H,、的延长线交于E,给出下列结论: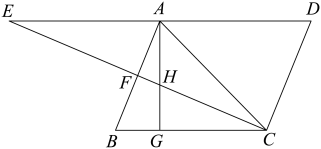
①; ②;
③; ④若点F是的中点,则;
其中正确的结论有( ).
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 若二次根式 有意义,则x的取值范围是 .14. 两台A、B型号的大米自动封装机包装的质量为的袋食品中各封装了10袋大米,测得其实际质量如下表(单位:):
A
B
由上表可以判断型号自动封装机性能更好.
15. 已知直线 , 当时必有 , 则k的值可以是(写出满足条件的一个值即可).16. 在正方形中, , 点E、F分别为上一点,且 , 连接 , 则的最小值是 .
三、解答题
-
17. 计算(1)、下面是小华同学解答题目的过程:
第一步.
第二步.
第三步.
第四步.
小华的解题过程是否有错误?如果有,请指出在第几步出现错误,并从这一步开始写出正确解答过程.
(2)、18. 如图,已知是矩形的对角线.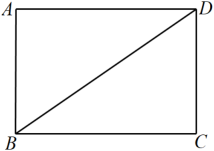 (1)、用直尺和圆规作线段的垂直平分线,分别交于E、F(保留作图痕迹,不写作法和证明);(2)、连接 , 若 , 求的度数.19. 新冠过后人们的生活逐渐恢复正常,家长们会选择去自然环境较好的地方“遛娃”.如图所示,是无动力游乐场内一个小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线上,转轴中心B到地面的距离为 . 在荡秋千过程中,当秋千摆动到最高点A时,测得点A到的距离为 , 点A到地面的距离为;当从A处摆动到处时,有 .
(1)、用直尺和圆规作线段的垂直平分线,分别交于E、F(保留作图痕迹,不写作法和证明);(2)、连接 , 若 , 求的度数.19. 新冠过后人们的生活逐渐恢复正常,家长们会选择去自然环境较好的地方“遛娃”.如图所示,是无动力游乐场内一个小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线上,转轴中心B到地面的距离为 . 在荡秋千过程中,当秋千摆动到最高点A时,测得点A到的距离为 , 点A到地面的距离为;当从A处摆动到处时,有 .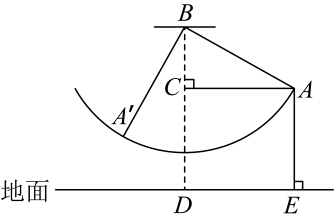 (1)、求到的距离;(2)、求到地面的距离.20. 《中华人民共和国国家安全法》规定,“中华人民共和国公民有维护国家的安全、荣誉和利益的义务,不得有危害国家的安全、荣誉和利益的行为.”2014年4月15日,习近平总书记强调,要准确把握国家安全形势变化新特点新趋势,坚持总体国家安全观,走出一条中国特色国家安全道路.某校为了了解全校学生对国家安全相关知识的掌握情况,特组织了一次国家安全知识竞赛,每班选25名同学参加比赛,成绩分为A、B、C、D四个等级,对应的分数依次为100分、90分、80分、70分.学校将七年级1班和2班的成绩整理并绘制如图的统计图:
(1)、求到的距离;(2)、求到地面的距离.20. 《中华人民共和国国家安全法》规定,“中华人民共和国公民有维护国家的安全、荣誉和利益的义务,不得有危害国家的安全、荣誉和利益的行为.”2014年4月15日,习近平总书记强调,要准确把握国家安全形势变化新特点新趋势,坚持总体国家安全观,走出一条中国特色国家安全道路.某校为了了解全校学生对国家安全相关知识的掌握情况,特组织了一次国家安全知识竞赛,每班选25名同学参加比赛,成绩分为A、B、C、D四个等级,对应的分数依次为100分、90分、80分、70分.学校将七年级1班和2班的成绩整理并绘制如图的统计图: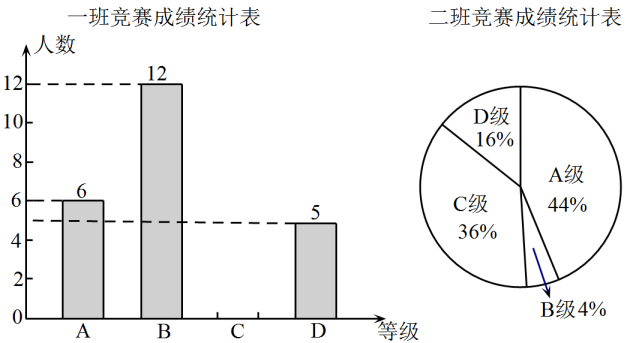 (1)、把竞赛成绩统计图补充完整;(2)、根据下表填空:;;;
(1)、把竞赛成绩统计图补充完整;(2)、根据下表填空:;;;平均数(分)
中位数(分)
众数(分)
一班
90
二班
87.6
80
(3)、请从平均数和中位数或众数中任选两个对这次竞赛成绩的结果进行分析.21. 某城建公司共有50台渣土运输车,其中甲型20台,乙型30台.现将这台渣土运输车全部配往两工地,其中30台派往A地,20台派往B地.两工地与城建公司商定的每天的租赁价格如下:甲型渣土车租金
乙型渣土车租金
A地
1800元/台
1600元/台
B地
1600元/台
1800元/台
(1)、设派往A地x台甲型渣土运输车,该城建公司这50台渣土车一天获得的租金为y(元),请求出y与x的函数解析式.(2)、若该城建公司这50台渣土运输车一天的租金总额不低于79600元,说明有多少种分派方案,并将各种方案写出.(3)、在(2)的条件下,选择哪种方案该城建公司一天获得租金最多?最多租金是多少?请说明理由.22. 如图1和图2所示,是等腰三角形, , 点P是底边上的一个动点(不与A,B重合),连接 .
 (1)、如图2所示,当平分时,求证: .(2)、如图1所示,当时,结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.23. 在解决数学问题时,我们一般先仔细阅读题干,找出有用信息作为已知条件,然后利用这些信息解决问题,但是有的题目信息比较明显,我们把这样的信息称为显性条件;而有的信息不太明显,需要结合图形、特殊式子成立的条件、实际问题等发现隐含信息作为条件,我们把这样的条件称为隐含条件;所以我们在做题时,要注意发现题目中的隐含条件.
(1)、如图2所示,当平分时,求证: .(2)、如图1所示,当时,结论还成立吗?若成立,请写出证明过程;若不成立,请说明理由.23. 在解决数学问题时,我们一般先仔细阅读题干,找出有用信息作为已知条件,然后利用这些信息解决问题,但是有的题目信息比较明显,我们把这样的信息称为显性条件;而有的信息不太明显,需要结合图形、特殊式子成立的条件、实际问题等发现隐含信息作为条件,我们把这样的条件称为隐含条件;所以我们在做题时,要注意发现题目中的隐含条件.阅读下面的解题过程,体会如何发现隐含条件并回答下面的问题.
化简: .
解:隐含条件 , 解得 ,
∴ ,
∴原式 .
(1)、试化简:;(2)、已知a、b满足 , 求的值.24. 如图,正方形中,是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线上移动,另一边交于Q.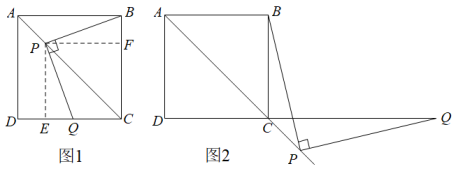 (1)、如图1,当点Q在边上时,探究与所满足的数量关系;
(1)、如图1,当点Q在边上时,探究与所满足的数量关系;小明同学探究此问题的方法是:过P点作于E点,于F点,根据正方形的性质和角平分线的性质,得出 , 再证明 , 可得出结论,他的结论应是 ;并证明该结论.
(2)、如图2,当点Q落在的延长线上时,猜想并写出与满足的数量关系,并证明你的猜想.25. 在平面直角坐标系中,我们将横纵坐标都是整数的点叫作整点.以P为顶点向右上方作各边垂直于坐标轴的正方形,若对于直线 , 此正方形内部(不包括边)有且仅有m个整点在直线上,则称该正方形为直线关于点P的“m类正方形”. (1)、已知点 , , , , 则正方形为直线关于点P的类正方形;(2)、若点是整点,正方形的边长为4,正方形为直线关于点P的1类正方形,则点B的坐标是;(3)、已知点P是整点且位于直线上.设直线关于点P的“3类正方形”的边长为a,求a的取值范围.
(1)、已知点 , , , , 则正方形为直线关于点P的类正方形;(2)、若点是整点,正方形的边长为4,正方形为直线关于点P的1类正方形,则点B的坐标是;(3)、已知点P是整点且位于直线上.设直线关于点P的“3类正方形”的边长为a,求a的取值范围.