山东省济南市历下区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-17 类型:期末考试
一、单选题
-
1. 4的平方根是( )A、 ±2 B、2 C、﹣2 D、162. 第31届世界大学生夏季运动会将于2023年7月28日在成都开幕.以下是历届世界大学生夏季运动会的标志,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,点E在的延长线上,下列条件中能判断的是( )
3. 如图,点E在的延长线上,下列条件中能判断的是( ) A、 B、 C、 D、4. 下表为一个图案中红色和白色瓷砖数量的关系.设r和w分别为红色和白色瓷砖的数量,下列函数表达式可以表示w与r之间的关系的是( )
A、 B、 C、 D、4. 下表为一个图案中红色和白色瓷砖数量的关系.设r和w分别为红色和白色瓷砖的数量,下列函数表达式可以表示w与r之间的关系的是( )红色瓷砖数量(r)
3
4
5
6
7
白色瓷砖数量(w)
6
8
10
12
14
A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 事件:“在只装有2个红球和6个黑球的袋子里,摸出一个白球”是( )A、不确定事件 B、随机事件 C、必然事件 D、不可能事件7. 如图, , 若 , 则的长度为( ) A、2 B、5 C、10 D、158. 如图,一个均匀的转盘被平均分成八等份,分别标有1,2,3,4,5,6,7,8这8个数字,转动转盘,当转盘停止后,指针指向的数字为“4的倍数”的概率为( )
A、2 B、5 C、10 D、158. 如图,一个均匀的转盘被平均分成八等份,分别标有1,2,3,4,5,6,7,8这8个数字,转动转盘,当转盘停止后,指针指向的数字为“4的倍数”的概率为( ) A、 B、 C、 D、9. 如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,甲船沿北偏西方向,以每小时12海里的速度航行;乙船沿北偏东方向,以每小时16海里的速度航行.1小时后两船分别位于点A与B处,此时两船相距( )
A、 B、 C、 D、9. 如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,甲船沿北偏西方向,以每小时12海里的速度航行;乙船沿北偏东方向,以每小时16海里的速度航行.1小时后两船分别位于点A与B处,此时两船相距( ) A、12海里 B、16海里 C、20海里 D、24海里10. 如图,在锐角三角形中,直线l为的中垂线,射线为的角平分线,且直线l与射线相交于点P.若 , 则的度数为( )
A、12海里 B、16海里 C、20海里 D、24海里10. 如图,在锐角三角形中,直线l为的中垂线,射线为的角平分线,且直线l与射线相交于点P.若 , 则的度数为( )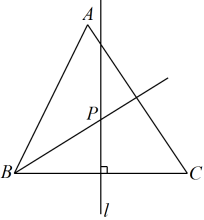 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. .12. 如图,直线与相交于点O,如果 , 那么是度.
 13. 如图,是的中线, , 和的周长的差是 .
13. 如图,是的中线, , 和的周长的差是 . 14. 一个袋子中装有12个红球和若干个白球,每个球除颜色外都相同,从中任意摸出一个球,如果摸出白球的概率是 , 则白球的数量为个.15. 如图,在中, , 的垂直平分线交于点D,交于点E,已知的周长为 , , 则 .
14. 一个袋子中装有12个红球和若干个白球,每个球除颜色外都相同,从中任意摸出一个球,如果摸出白球的概率是 , 则白球的数量为个.15. 如图,在中, , 的垂直平分线交于点D,交于点E,已知的周长为 , , 则 . 16. 如图,小霞将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端12米处,发现此时绳子底端距离打结处约6米,则滑轮到地面的高度为米.
16. 如图,小霞将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端12米处,发现此时绳子底端距离打结处约6米,则滑轮到地面的高度为米.
三、解答题
-
17. 计算:(1)、(2)、18. 如图,在与中,与交于点E,且 . 试说明: .
 19. 先化简,再求值: . 其中 .20. 如图,在方格纸中,每个方格的边长为 .
19. 先化简,再求值: . 其中 .20. 如图,在方格纸中,每个方格的边长为 . (1)、画出四边形关于直线l对称的图形四边形;(2)、四边形的面积为;(3)、直线l上存在一点P,CP与之和最短,请画出P点的位置(保留作图痕迹).21. 如图,在四边形中, . 求四边形的面积.
(1)、画出四边形关于直线l对称的图形四边形;(2)、四边形的面积为;(3)、直线l上存在一点P,CP与之和最短,请画出P点的位置(保留作图痕迹).21. 如图,在四边形中, . 求四边形的面积. 22. 在中, , 为的角平分线, , 垂足为E, . 求的值.
22. 在中, , 为的角平分线, , 垂足为E, . 求的值. 23. 小蒙设计一个抽奖游戏:如图 , 宝箱由个方格组成,方格中随机放置着个奖品,每个方格最多能放一个奖品.
23. 小蒙设计一个抽奖游戏:如图 , 宝箱由个方格组成,方格中随机放置着个奖品,每个方格最多能放一个奖品. (1)、如果随机打开一个方格,获得奖品的概率是 .(2)、为了增加趣味性,小蒙优化了这个游戏.小雨参加游戏,第一次没有获得奖品,但是呈现了数字 , 如图 . 小蒙解释,这说明与这个方格相邻的个方格(即区域)中有两个放置了奖品,进行第二次抽奖,小雨将有两种选择,打开区域中的小方格,或者打开区域外的小方格.为了尽可能获得奖品,你建议小雨如何选择?请说明理由.24. 如图,A中学位于南北向公路l的一侧,门前有两条长度均为100米的小路通往公路l,与公路l交于B,C两点,且B,C相距120米.
(1)、如果随机打开一个方格,获得奖品的概率是 .(2)、为了增加趣味性,小蒙优化了这个游戏.小雨参加游戏,第一次没有获得奖品,但是呈现了数字 , 如图 . 小蒙解释,这说明与这个方格相邻的个方格(即区域)中有两个放置了奖品,进行第二次抽奖,小雨将有两种选择,打开区域中的小方格,或者打开区域外的小方格.为了尽可能获得奖品,你建议小雨如何选择?请说明理由.24. 如图,A中学位于南北向公路l的一侧,门前有两条长度均为100米的小路通往公路l,与公路l交于B,C两点,且B,C相距120米. (1)、现在想修一条从公路l到A中学的新路(点D在l上),使得学生从公路l走到学校路程最短,应该如何修路(请在图中画出)?新路长度是多少?(2)、为了行车安全,在公路l上的点B和点E处设置了一组区间测速装置,其中点E在点B的北侧,且距A中学170米.一辆车经过区间用时5秒,若公路l限速为(约),请判断该车是否超速,并说明理由.25. 如图1,两条互相垂直的公路m、n,十字路口记作点A.小海从公路m上的点B出发,骑车向北匀速直行,中途遇上红灯(忽略停车与起步的速度变化);同时,小丹从点A出发,沿公路n步行向东匀速直行.设出发时间为t(分钟),两人与点A的距离为S(米).图2是两人与路口的距离S(米)与运动时间t(分钟)之间的关系图.
(1)、现在想修一条从公路l到A中学的新路(点D在l上),使得学生从公路l走到学校路程最短,应该如何修路(请在图中画出)?新路长度是多少?(2)、为了行车安全,在公路l上的点B和点E处设置了一组区间测速装置,其中点E在点B的北侧,且距A中学170米.一辆车经过区间用时5秒,若公路l限速为(约),请判断该车是否超速,并说明理由.25. 如图1,两条互相垂直的公路m、n,十字路口记作点A.小海从公路m上的点B出发,骑车向北匀速直行,中途遇上红灯(忽略停车与起步的速度变化);同时,小丹从点A出发,沿公路n步行向东匀速直行.设出发时间为t(分钟),两人与点A的距离为S(米).图2是两人与路口的距离S(米)与运动时间t(分钟)之间的关系图. (1)、两点之间的距离为米,小海等红灯的时间为分钟;(2)、当小海等红灯时,此时小丹前进了米;(3)、求小海经过路口A后S与t的关系式;(4)、当两人距离路口A距离相等时,直接写出运动时间.26. 小琳在学习等腰三角形性质“三线合一”时,发现:
(1)、两点之间的距离为米,小海等红灯的时间为分钟;(2)、当小海等红灯时,此时小丹前进了米;(3)、求小海经过路口A后S与t的关系式;(4)、当两人距离路口A距离相等时,直接写出运动时间.26. 小琳在学习等腰三角形性质“三线合一”时,发现: (1)、如图1,在中,若 , 可以得出 . 请你用所学知识证明此结论.(2)、小琳提出了一个问题:如图2,如果 , 能不能说明?小琳不知道这个问题如何解决,便询问老师,老师进行了指导:条件里有“”和“”,我们可以尝试将和 “变成”一条线段,将和 “变成”一条线段,为了确保的条件可以使用,和的位置最好不要改变,所以我们可以“延长至E,使 , 延长至F,使”.老师指导后,小琳还是没有思路.请你帮助小琳,完成问题的解答,(3)、小琳又提出了新的问题:如图3,如果 , 能不能说明?请你帮助小琳,完成问题的解答.
(1)、如图1,在中,若 , 可以得出 . 请你用所学知识证明此结论.(2)、小琳提出了一个问题:如图2,如果 , 能不能说明?小琳不知道这个问题如何解决,便询问老师,老师进行了指导:条件里有“”和“”,我们可以尝试将和 “变成”一条线段,将和 “变成”一条线段,为了确保的条件可以使用,和的位置最好不要改变,所以我们可以“延长至E,使 , 延长至F,使”.老师指导后,小琳还是没有思路.请你帮助小琳,完成问题的解答,(3)、小琳又提出了新的问题:如图3,如果 , 能不能说明?请你帮助小琳,完成问题的解答.