山东省济南市市中区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-17 类型:期末考试
一、单选题
-
1. 下列长度的三条线段能组成三角形的是( )A、3cm , 5cm , 7cm B、3cm , 3cm , 7cm C、4cm , 4cm , 8cm D、4cm , 5cm , 9cm2. 中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录.下列四幅作品分别代表“立春”、“谷雨”、“立夏”、“小满”,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 中芯国际集成电路制造有限公司,是中国内地技术最先进、配套最完善、规模最大的集成电路制造企业集团,中芯国际第一代14纳米FinFET技术取得了突破性进展,并于2019年第四季度进入量产,代表了中国大陆自主研发集成电路的最先进水平,14纳米米,用科学记数法表示为( )A、 B、 C、 D、4. 下列事件中是必然事件的是( )A、投掷一次骰子,向上一面的点数是6 B、清明时节雨纷纷 C、任意画一个三角形,其内角和是 D、经过有红绿灯的路口,遇到红灯5. 星期天,小王去朋友家借书,他离家的距离与时间的函数图象如图所示,根据图象信息,下列说法正确的是( )
3. 中芯国际集成电路制造有限公司,是中国内地技术最先进、配套最完善、规模最大的集成电路制造企业集团,中芯国际第一代14纳米FinFET技术取得了突破性进展,并于2019年第四季度进入量产,代表了中国大陆自主研发集成电路的最先进水平,14纳米米,用科学记数法表示为( )A、 B、 C、 D、4. 下列事件中是必然事件的是( )A、投掷一次骰子,向上一面的点数是6 B、清明时节雨纷纷 C、任意画一个三角形,其内角和是 D、经过有红绿灯的路口,遇到红灯5. 星期天,小王去朋友家借书,他离家的距离与时间的函数图象如图所示,根据图象信息,下列说法正确的是( )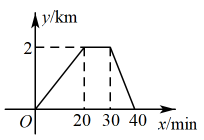 A、小王去时的速度大于回家的速度 B、小王在朋友家停留了10分钟 C、小王去时所花的时间少于回家所花的时间 D、小王去时走上坡路,回家时走下坡路6. 如图, , , 平分 , 则的度数为( )
A、小王去时的速度大于回家的速度 B、小王在朋友家停留了10分钟 C、小王去时所花的时间少于回家所花的时间 D、小王去时走上坡路,回家时走下坡路6. 如图, , , 平分 , 则的度数为( )
 A、 B、 C、 D、7. 下列运算正确的是( )A、 B、 C、 D、8. 下列命题中是真命题的是( )A、相等的角是对顶角 B、若 , 则 C、内错角相等 D、在同一平面内,过一点有且只有一条直线与已知直线垂直;9. 如图,在中, , 图中所作直线与射线交于点D,点D在边上,根据图中尺规作图痕迹,判断以下结论正确的是( )
A、 B、 C、 D、7. 下列运算正确的是( )A、 B、 C、 D、8. 下列命题中是真命题的是( )A、相等的角是对顶角 B、若 , 则 C、内错角相等 D、在同一平面内,过一点有且只有一条直线与已知直线垂直;9. 如图,在中, , 图中所作直线与射线交于点D,点D在边上,根据图中尺规作图痕迹,判断以下结论正确的是( ) A、 B、 C、 D、10. 如图,在Rt△ABC中, , AC=6,BC=8,AB=10,AD是的平分线,若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
A、 B、 C、 D、10. 如图,在Rt△ABC中, , AC=6,BC=8,AB=10,AD是的平分线,若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( ) A、2.4 B、4 C、4.8 D、5
A、2.4 B、4 C、4.8 D、5二、填空题
-
11. 填空:(a3)4= .12. 正方形地板由9块边长均相等的小正方形组成,米粒随机地撒在如图所示的正方形地板上,那么米粒最终停留在黑色区域的概率是
 13. 如图,公园里有一座假山,要测量假山两端、的距离,先在平地上取一个可以直接到达、的点 , 分别延长、 , 到、 , 使 , , 连接 , 这样就可以利用三角形全等,通过测量的长得到假山两端、的距离,则这两个三角形全等的依据是 .
13. 如图,公园里有一座假山,要测量假山两端、的距离,先在平地上取一个可以直接到达、的点 , 分别延长、 , 到、 , 使 , , 连接 , 这样就可以利用三角形全等,通过测量的长得到假山两端、的距离,则这两个三角形全等的依据是 . 14. 地表以下岩层的温度y()随着所处深度x()的变化而变化,在某地点y与x之间有如下关系:
14. 地表以下岩层的温度y()随着所处深度x()的变化而变化,在某地点y与x之间有如下关系:1
2
3
4
55
90
125
160
那么y与x之间的关系式为 .
15. 若 , , 则的值为 .16. 如图,是等边三角形,是等腰直角三角形, , 于点 , 连接分别交 , 于点 , , 过点作分别交 , 于点 , , 则下列结论正确的是 .①;②;③;④

三、解答题
-
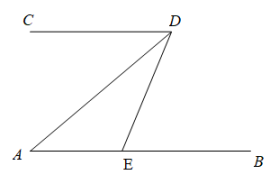
17.(1)、;(2)、化简: .18. 计算:先化简,再求值: , 其中 , .19. 如图,点A,D,B,E在同一直线上, . 求证: .
 20. 如图所示,在正方形网格上有一个△ABC.
20. 如图所示,在正方形网格上有一个△ABC. (1)、作△ABC关于直线MN的对称图形;(不写作法)(2)、在MN上找到一点P,使得PA+PC最小;(3)、若网格上的最小正方形边长为1,求△ABC的面积.21. 如图,点E、F分别在AB、CD上,于点O, , , 求证: .
(1)、作△ABC关于直线MN的对称图形;(不写作法)(2)、在MN上找到一点P,使得PA+PC最小;(3)、若网格上的最小正方形边长为1,求△ABC的面积.21. 如图,点E、F分别在AB、CD上,于点O, , , 求证: .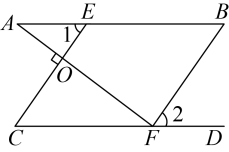
证明:∵(已知),
∴ ▲
又∵(已知),
∴ ▲ (同位角相等,两直线平行),
∴( ),
∴ ▲
又∵ ▲ (平角的定义)
∴ ▲ ,
又∵(已知),
∴( ),
∴( )
22. 在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的球,其中红球3个,白球5个,黑球若干个.若从中任意摸出一个白球的概率是 .(1)、求盒子中黑球的个数;(2)、求任意摸出一个球是黑球的概率;(3)、能否通过只改变盒子中白球的数量,使得任意摸出一个球是红球的概率为 , 若能,请写出如何调整白球数量.23. 充满未来感、时代感、速度感的2022年北京冬奥会吉祥物“冰墩墩”火遍全球,为了满足广大需求,某冰墩墩生产厂家引进新设备,让新旧设备同时生产,提高冰墩墩的产量.如图所示,甲表示新设备的产量y(万个)与时间x(天)的关系,乙表示旧设备的产量y(万个)与时间x(天)的关系. (1)、由图象可知,新设备因故停止生产了天;(2)、在正常生产的情况下,分别求新、旧设备每天生产冰墩墩的个数;(3)、试问:第几天新、旧设备所生产的冰墩墩的数量相同?
(1)、由图象可知,新设备因故停止生产了天;(2)、在正常生产的情况下,分别求新、旧设备每天生产冰墩墩的个数;(3)、试问:第几天新、旧设备所生产的冰墩墩的数量相同?