湖南省湘西州凤凰县2022—2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-07-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，是无理数的是（）

A、 $- 1$ B、 $\sqrt{4}$ C、 $\sqrt{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 点P（2，1）在平面直角坐标系中所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 如图，点E在 $A C$ 的延长线上，下列条件中能判断 $A B ∥ C D$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 = ∠ 4$ C、 $∠ D = ∠ D C E$ D、 $∠ D + ∠ D C A = 180 °$

查看试题解析
4. 若 ${\begin{array}{l} x = 1 \\ y = - 2 \end{array}$ 是关于x和y的二元一次方程 $a x + y = 2$ 的解，则a的值等于（）

A、0 B、1 C、2 D、4

查看试题解析
5. 下列是真命题的是（）

A、有理数与数轴上的点一一对应 B、内错角相等 C、同一平面内，垂直于同一条直线的两条直线互相平行 D、负数没有立方根

查看试题解析
6. 若x>y，则下列式子中错误的是（）

A、x－3>y－3 B、 $\frac{x}{3} > \frac{y}{3}$ C、x+3>y+3 D、－3x>－3y

查看试题解析
7. 将点 $P (- 5 ， 4)$ 向右平移4个单位，向上平移2个单位，得到点P的对应点 $P^{'}$ 的坐标是（）

A、 $(- 5 ， 8)$ B、 $(- 1 ， 2)$ C、 $(- 1 ， 6)$ D、 $(- 5 ， 0)$

查看试题解析
8. 下列调查中，适合采用全面调查（普查）方式的是（）

A、对綦江河水质情况的调查 B、对端午节期间市场上粽子质量情况的调查 C、对某班50名同学体重情况的调查 D、对某类烟花爆竹燃放安全情况的调查

查看试题解析
9. 过点 $A$ 画线段 $B C$ 所在直线的垂线段，其中正确的是（）

A、 B、 C、 D、

查看试题解析
10. 《九章算术》中有这样一个题：今有甲乙二人持钱不知其数.甲得乙半而钱五十，乙得甲太半而钱亦五十.问甲、乙持钱各几何？其意思为：今有甲乙二人，不如其钱包里有多少钱，若乙把其一半的钱给甲，则甲的数为50；而甲把其 $\frac{2}{3}$ 的钱给乙，则乙的钱数也为50，问甲、乙各有多少钱？设甲的钱数为x，乙的钱数为y，则可建立方程组为（）

A、 ${\begin{cases} x + \frac{1}{2} y = 50 \\ \frac{2}{3} x + y = 50 \end{cases}$ B、 ${\begin{cases} x + \frac{1}{2} y = 50 \\ x + \frac{2}{3} y = 50 \end{cases}$ C、 ${\begin{cases} \frac{1}{2} x + y = 50 \\ \frac{2}{3} x + y = 50 \end{cases}$ D、 ${\begin{cases} \frac{1}{2} x + y = 50 \\ x + \frac{2}{3} y = 50 \end{cases}$

查看试题解析

二、填空题

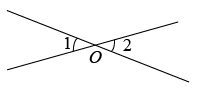
11. 9的算术平方根是．

查看试题解析
12. 若 $(x - 3)^{2} + \sqrt{y + 2} = 0$ ，则 $x + y$ = ．

查看试题解析
13. 如图，两条直线相交于点O，若 $∠ 1 + ∠ 2 = 64 °$ ，则 $∠ 1 =$ 度．

查看试题解析
14. 若 $x^{| a | - 1} + (a - 2) y = 1$ 是关于x，y的二元一次方程，则 $a =$ ．

查看试题解析
15. 用不等式表示：a与2的差大于-1 ．

查看试题解析
16. 物理中有一种现象，叫折射现象，它指的是当光线从空气射入水中时，光线的传播方向会发生改变．如图，我们建立折射现象数学模型， $M N$ 表示水面，它与底面 $E F$ 平行，光线 $A B$ 从空气射入水里时发生了折射，变成光线 $B C$ 射到水底 $C$ 处，射线 $B D$ 是光线 $A B$ 的延长线， $∠ 1 = 70 °$ ， $∠ 2 = 42 °$ ，则 $∠ D B C$ 的度数为°．

查看试题解析
17. 平移变换不仅与几何图形有着密切的联系，而且在一些特殊结构的汉字中，也有平移变换的现象，如：“日”“朋”“森”等，请你再写两个具有平移变换现象的汉字．

查看试题解析
18. 教材在第七章复习题的“拓广探索”中，曾让同学们探索发现：在平面直角坐标系中，线段中点的横坐标（纵坐标）分别等于对应线段的两个端点的横坐标（纵坐标）和的一半，例如：点 $A (1 ， 3)$ ，点 $B (7 ， 1)$ ，则线段 $A B$ 的中点 $M$ 的坐标为 $(4 ， 2)$ ，请利用以上结论解决问题：在平面直角坐标系中，点 $E (a + 3 ， a)$ ， $F (b ， a + b + 1)$ 若线段 $E F$ 的中点 $G$ 恰好在 $x$ 轴上，且到 $y$ 轴的距离是 $3$ ，则 $a - b =$ ．

查看试题解析

三、解答题

19. 计算： $| - \sqrt{3} | + \sqrt{(- 3)^{2}} - {(- 1)}^{2023} + \sqrt[3]{- 27}$ ．

查看试题解析
20. 解不等式组 ${\begin{array}{l} x - 2 (x - 1) \leq 2 \\ \frac{1 + x}{3} > x - 1 \end{array}$ ，并将不等式组的解集在数轴上表示出来．

查看试题解析
21. 解方程组： ${\begin{array}{l} x - y = 3 \\ 7 x + 5 y = - 9 \end{array}$

查看试题解析
22. 如图，已知直线 $B D$ 分别交射线 $A E$ ， $C F$ 于点 $B$ ， $D$ ，连接 $A D$ 和 $B C$ ， $A D ∥ B C$ ， $∠ A = ∠ C$ ．试说明： $∠ 1 + ∠ 2 = 180 °$ ．
∵ $A D ∥ B C$ ．（已知），∴ $∠ A = ∠ C B E$ （  ），
∵ $∠ A = ∠ C$ （  ），∴ $∠ C =$        ▲       （  ），
∴       ▲   $∥ C D$ （  ），
∴ $∠ A B D +$        ▲   $= 180 °$ （两直线平行，同旁内角互补），
∵ $∠ A B D =$        ▲  ， $∠ B D F = ∠ 2$ （对顶角相等），
∴ $∠ 1 + ∠ 2 = 180 °$ ．

查看试题解析
23. 我校九年级163班所有学生参加体育测试，根据测试评分标准，将他们的成绩进行统计后分为A、B、C、D四等，并绘制成如图所示的条形统计图和扇形统计图（未完成），请结合图中所给信息解答下列问题：

(1)、九年级163班参加体育测试的学生共有多少人？

(2)、将条形统计图补充完整；

(3)、在扇形统计图中，求出等级C对应的圆心角的度数；

(4)、若规定达到A、B级为优秀，我校九年级共有学生850人，估计参加体育测试达到优秀标准的学生有多少人？

查看试题解析
24. 某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求，决定增设篮球、足球两门选修课程，需要购进一批篮球和足球．已知购买2个篮球和3个足球共需费用510元；购买3个篮球和5个足球共需费用810元．

(1)、求篮球和足球的单价分别是多少元；

(2)、学校计划采购篮球、足球共50个，并要求篮球不少于30个，且总费用不超过5500元．那么有哪几种购买方案？并求出最省钱的购买方案

查看试题解析
25. 我们定义，关于同一个未知数的不等式A和B，两个不等式的解集相同，则称A与B为同解不等式．

(1)、若关于x的不等式A： $1 - 3 x > 0$ ，不等式B： $\frac{3 x + a}{2} < 1$ 是同解不等式，求a的值；

(2)、若关于x的不等式C： $x + 1 > m n$ ，不等式D： $x - 3 > m$ 是同解不等式，其中m，n是正整数，求m，n的值；

(3)、若关于x的不等式P： $(2 a - b) x + 3 a - 4 b < 0$ ，不等式Q： $\frac{14 x - 1}{2} > \frac{7}{2} - 2 x$ 是同解不等式，试求关于x的不等式 $(a - 4 b) x + 2 a - 3 b < 0$ 的解集．

查看试题解析
26. 如图1，在长方形 $O A B C$ 中， $O$ 为平面直角坐标系的原点， $O A = 2$ ， $O C = 4$ ，点 $B$ 在第一象限．

(1)、点 $B$ 的坐标为；

(2)、如图2，点 $P$ 是线段 $C B$ 延长线上的点，连接 $A P$ ， $O P$ ，则 $∠ P O C$ ， $∠ A P O$ ， $∠ P A B$ 三个角满足的关系是什么？并说明理由；

(3)、在（2）的基础上，已知： $∠ P A B = 20 °$ ， $∠ P O C = 50 °$ ，在第一象限内取一点 $F$ ，连接 $O F$ ， $A F$ ，满足 $∠ P A B = 2 ∠ F A P$ ， $∠ P O C = 2 ∠ F O P$ ，请直接写出 $\frac{∠ A P O}{∠ A F O}$ 的值．

查看试题解析