山东省聊城市东阿三中等四校联考2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-07-17 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，经过刨平的木板上的两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（）

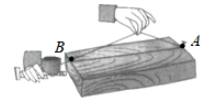A、两点确定一条直线 B、两点之间线段最短 C、垂线段最短 D、连接两点的线段叫做两点的距离

查看试题解析
2. 若关于x，y的方程组 ${\begin{array}{l} 3 x + 4 y = 8 ， \\ m x + (2 m - 1) y = 7 \end{array}$ 的解也是二元一次方程 $x - 2 y = 1$ 的解，则m的值为（）

A、 $\frac{5}{2}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、1

查看试题解析
3. 已知三条线段长分别为 $3 c m$ 、 $4 c m$ 、 $a c m$ ，若这三条线段首尾顺次连接能围成一个三角形，那么 $a$ 的取值范围是（ )

A、 $1 c m < a < 5 c m$ B、 $2 c m < a < 6 c m$ C、 $4 c m < a < 7 c m$ D、 $1 c m < a < 7 c m$

查看试题解析
4. 如图，下面说法正确的是（）

A、小红家在广场东偏北60°方向上，距离300米处 B、广场在学校南偏东35°方向上，距离200米处 C、广场在小红家东偏北30°方向上，距离300米处 D、学校在广场北偏西35°方向上，距离200米处

查看试题解析
5. 某H品牌手机上使用5nm芯片，1nm＝0.0000001cm，则5nm用科学记数法表示为（）

A、 $50 \times 10^{- 8} c m$ B、 $0.5 \times 10^{- 7} c m$ C、 $5 \times 10^{- 7} c m$ D、 $5 \times 10^{- 8} c m$

查看试题解析
6. 下列计算正确的是（）

A、 $a^{3} \cdot a^{3} = 2 a^{3}$ B、 ${(- a^{4})}^{5} = {(- a^{5})}^{4}$ C、 ${(x - y)}^{6} \div {(x - y)}^{3} = {(x - y)}^{2}$ D、 ${(- 0.2)}^{5} \times 5^{5} = - 1$

查看试题解析
7. 下列从左到右是因式分解且正确的是（）

A、 $x^{2} - 4 = {(x - 2)}^{2}$ B、 ${(x + 1)}^{2} = x^{2} + 2 x + 1$ C、 $x^{2} - 4 - 4 x = (x - 2) (x + 2) - 4 x$ D、 $x y + x = x (y + 1)$

查看试题解析
8. 若点 $P$ 在第二象限，且到 $x$ 轴的距离是3，到 $y$ 轴的距离是1，则点 $P$ 的坐标是（）

A、 $(3 ， 1)$ B、 $(- 1 ， 3)$ C、 $(- 1 ， - 3)$ D、 $(- 3 ， 1)$

查看试题解析
9. 若 $(x^{2} + a x + 2) (2 x - 4)$ 的结果中不含 $x^{2}$ 项，则 $a$ 的值为（）

A、 $0$ B、 $2$ C、 $\frac{1}{2}$ D、 $- 2$

查看试题解析
10. 如图，在△ABC中，作BC边上的高线，下列画法正确的是（）

A、 B、 C、 D、

查看试题解析
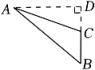11. 在边长为a的正方形中挖去一个边长为b的小正方形（ $a > b$ ）（如图甲），把余下的部分拼成一个矩形（如图乙），根据两个图形中阴影部分的面积相等，可以验证（）

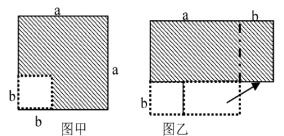A、 $a^{2} - b^{2} = (a + b) (a - b)$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $(a + 2 b) (a - b) = a^{2} + a b - 2 b^{2}$

查看试题解析
12. 如图，在△ABC中，G是边BC上任意一点，D、E、F分别是AG、BD、CE的中点，S_△ABC＝48，则S_△DEF的值为（　　）

A、4.8 B、6 C、8 D、12

查看试题解析

二、填空题

13. 计算： ${(π - 1)}^{0} + | - 2 | =$ .

查看试题解析
14. 在平面直角坐标系中，点 $(2 a + 1 ， 2 a - 1)$ 在 $x$ 轴上，则 $a$ 的值为．

查看试题解析
15. 若一个多边形的外角和比这个多边形的内角和小540°，则这个多边形的边数为.

查看试题解析
16. 已知 $x + y = 2 ， x y = - 1 ， (x - y)^{2} =$ ．

查看试题解析
17. 如图，直线 $a ∥ b$ ，含 $30 °$ 角的直角三角板 $A B C$ 的直角顶点C在直线b上，若 $∠ 1 = 40 °$ ，则 $∠ 2$ 的度数为 $°$ ．

查看试题解析

三、解答题

18. 计算：

(1)、(-a²)³÷a⁴+(a+2)(2a-3)．

(2)、(3a+2b-5)(3a-2b+5)

查看试题解析
19.

(1)、解方程组： ${\begin{array}{l} 3 x + 2 y = 12 ① \\ 2 x - y = 1 ② \end{array}$ ；

(2)、解方程组： ${\begin{array}{l} 4 x + y = 5 ① \\ \frac{x - 1}{2} + \frac{y}{3} = 2 ② \end{array}$ ．

查看试题解析
20. 因式分解：

(1)、 $x^{3} - 9 x$ ；

(2)、 $x^{2} y + 2 x y + y$ ；

(3)、 $2 a (x - y) - 6 b (y - x)$ ；

(4)、 ${(y^{2} - 1)}^{2} - 6 (y^{2} - 1) + 9$ ．

查看试题解析
21. 先化简，再求值： $(x - 2 y)^{2} + (x - 2 y) (x + 2 y) - 2 x (x - y)$ ，其中 $x = - \frac{3}{8}$ ， $y = 4$ ．

查看试题解析
22. 随着“低碳生活，绿色出行”理念的普及，新能源汽车正逐渐成为人们喜爱的交通工具，某汽车4S店计划购进一批新能源汽车进行销售.据了解，购进3辆A型新能源汽车、2辆B型新能源汽车的共需95万元；购进4辆A型新能源汽车、1辆B型新能源汽车的共需110万元.

(1)、问A、B两种型号的新能源汽车每辆进价分别为多少万元？

(2)、若该公司计划正好用250万元购进以上两种型号的新能源汽车（两种型号的汽车均购买），销售1辆A型汽车可获利1.2元，销售1辆B型汽车可获利0.8元，假如这些新能源汽车全部售出，问该公司的共有几种购买方案？最大利润是多少元？

查看试题解析
23. 如图，在直角坐标平面内，点A、B、C都是格点

(1)、写出图中点A、B、C的坐标是：A ， B ， C ．

(2)、 $△ A B C$ 的面积是

(3)、如果点P在x轴的正半轴上，且 $S_{Δ P A B} = \frac{18}{13} S_{Δ A B C}$ ，那么点P的坐标是．

查看试题解析
24. 探索发现：如图是一种网红弹弓的实物图，在两头上系上皮筋，拉动皮筋可形成平面示意图如下图①，弹弓的两边可看成是平行的，即AB∥CD，各活动小组探索∠APC与∠A，∠C之间的数量关系．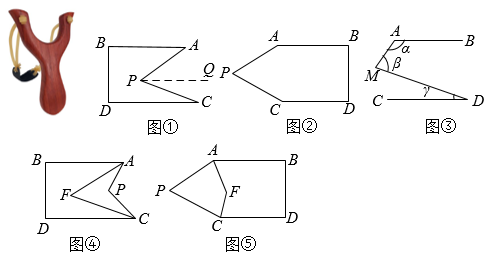

(1)、已知AB∥CD，点P不在直线AB和直线CD上，在图①中，智慧小组发现：∠APC＝∠A+∠C．
智慧小组是这样思考的：过点P作PQ∥AB⋯
请你按照智慧小组作的辅助线补全推理过程．

(2)、类比思考：
①在图②中，∠APC与∠A、∠C之间的数量关系为；
②如图③，已知AB∥CD，则∠α、∠β、∠γ之间的数量关系为．

(3)、解决问题：善思小组提出：如图④⑤，AB∥CD，AF、CF分别平分∠BAP、∠DCP．请分别求出图④、图⑤中，∠AFC与∠APC之间的数量关系，并说明理由．

查看试题解析