山东省聊城市东阿县2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-17 类型:期末考试
一、单选题
-
1. 下列图形中,能用 , , 三种表示方法表示同一个角的是( )A、
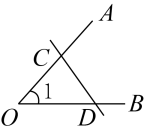 B、
B、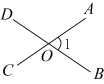 C、
C、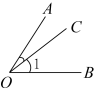 D、
D、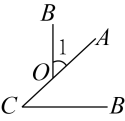 2. 如图 , , 平分 , 则的度数是( )
2. 如图 , , 平分 , 则的度数是( ) A、 B、 C、 D、3. 下列说法:①两点确定一条直线;②两点之间,线段最短;③若 , 则射线是的平分线;④连接两点之间的线段叫做这两点间的距离;⑤学校在小明家南偏东方向上,则小明家在学校北偏西方向上.其中正确的有( )A、1个 B、2个 C、3个 D、4个4. 下列说法中,正确的是( )A、一个锐角的补角大于这个角的余角 B、一对互补的角中,一定有一个角是锐角 C、锐角的余角一定是钝角 D、锐角的补角一定是锐角5. 若关于x,y的二元一次方程组 的解也是二元一次方程2x+3y=6的解,则k的值为( )A、﹣ B、 C、 D、﹣6. 如图,三个天平的托盘中形状相同的物体质量相等.图①、图②所示的两个天平处于平衡状态,要使第三个天平也保持平衡,可在它的右盘中放置( )
A、 B、 C、 D、3. 下列说法:①两点确定一条直线;②两点之间,线段最短;③若 , 则射线是的平分线;④连接两点之间的线段叫做这两点间的距离;⑤学校在小明家南偏东方向上,则小明家在学校北偏西方向上.其中正确的有( )A、1个 B、2个 C、3个 D、4个4. 下列说法中,正确的是( )A、一个锐角的补角大于这个角的余角 B、一对互补的角中,一定有一个角是锐角 C、锐角的余角一定是钝角 D、锐角的补角一定是锐角5. 若关于x,y的二元一次方程组 的解也是二元一次方程2x+3y=6的解,则k的值为( )A、﹣ B、 C、 D、﹣6. 如图,三个天平的托盘中形状相同的物体质量相等.图①、图②所示的两个天平处于平衡状态,要使第三个天平也保持平衡,可在它的右盘中放置( ) A、3个球 B、4个球 C、5个球 D、6个球7. 学校组织植树活动,已知在甲处植树的有48人,在乙处植树的有42人,由于甲处植树任务较重,需调配部分乙处的人员去甲处支援,使在甲处植树的人数是乙处植树人数的2倍,设从乙处调配x人去甲处,则( )A、48=2(42-x) B、48+x=2×42 C、48-x=2(42+x) D、48+x=2(42-x)8. 已知 ,则 的值为( )A、40 B、80 C、160 D、2409. 纳米时一种极小的长度单位, , 已知一种病毒的直径约为 , 则用科学记数法表示该病毒的直径为( )A、 B、 C、 D、10. 若是完全平方式,则的值应是( )A、16或 B、18 C、 D、18或11. 已知轴,且点A的坐标为 , 点B的坐标为 , 则点A的坐标为( )A、 B、 C、 D、12. 下列数据中不能确定物体的位置的是( )A、南偏西40° B、红旗小区3号楼701号 C、龙山路461号 D、东经130°,北纬54°
A、3个球 B、4个球 C、5个球 D、6个球7. 学校组织植树活动,已知在甲处植树的有48人,在乙处植树的有42人,由于甲处植树任务较重,需调配部分乙处的人员去甲处支援,使在甲处植树的人数是乙处植树人数的2倍,设从乙处调配x人去甲处,则( )A、48=2(42-x) B、48+x=2×42 C、48-x=2(42+x) D、48+x=2(42-x)8. 已知 ,则 的值为( )A、40 B、80 C、160 D、2409. 纳米时一种极小的长度单位, , 已知一种病毒的直径约为 , 则用科学记数法表示该病毒的直径为( )A、 B、 C、 D、10. 若是完全平方式,则的值应是( )A、16或 B、18 C、 D、18或11. 已知轴,且点A的坐标为 , 点B的坐标为 , 则点A的坐标为( )A、 B、 C、 D、12. 下列数据中不能确定物体的位置的是( )A、南偏西40° B、红旗小区3号楼701号 C、龙山路461号 D、东经130°,北纬54°二、填空题
-
13. 将一副直角三角板如图放置,使含角的三角板的短直角边和含角的三角板的一条直角边重合,则的余角的度数是 .
 14. 如图,直线、相交于点 , 平分 , 若 , 则的度数是 .
14. 如图,直线、相交于点 , 平分 , 若 , 则的度数是 .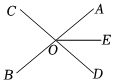 15. 如图,中, , P为直线上一动点,连 , 则线段的最小值是 .
15. 如图,中, , P为直线上一动点,连 , 则线段的最小值是 . 16. 已知方程是关于 , 的二元一次方程,则 .17. 计算(x2+nx+3)(x2﹣3x)的结果不含x2的项,那么n=18. 若和的积与是同类项,则的值为 .19. 在平面直角坐标系xOy中,点M的坐标是(1,2),轴, , 则点N的坐标是 .20. 探索题:
16. 已知方程是关于 , 的二元一次方程,则 .17. 计算(x2+nx+3)(x2﹣3x)的结果不含x2的项,那么n=18. 若和的积与是同类项,则的值为 .19. 在平面直角坐标系xOy中,点M的坐标是(1,2),轴, , 则点N的坐标是 .20. 探索题:;
;
;
;
根据前面的规律,回答问题:
当时, .
三、解答题
-
21.(1)、计算:;(2)、计算: .22. 因式分解:(1)、;(2)、;(3)、 .23. 阅读下面的材料,解决问题.
例题:若m2 +2mn+2n2-6n+9=0,求m和n的值.
解:∵ m2+2mn+2n2- 6n+9=0,
∴m2 +2mn+n2+n2-6n+9=0,
∴(m+n)2 +(n-3)2=0,
∴m+n=0, n-3=0,
∴m=-3, n=3.
问题:
(1)、若2x2 +4x-2xy+y2 +4=0,求xy的值;(2)、已知a, b, c是△ABC的三边长,且满足a2+b2=10a+8b-41,求c的取值范围.24. 利用二元一次方程组解应用题:某冬奥会纪念品专卖店计划同时购进“冰墩墩”和“雪容融”两种毛绒玩具,据了解,8只“冰墩墩”和10只“雪容融”的进价共计2000元;10只“冰墩墩”和20只“雪容融”的进价共计3100元,求“冰墩墩”和“雪容融”两种毛绒玩具每只进价分别是多少元.25. 如图,中, , , , . 若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm.设运动的时间为t秒. (1)、当t=时,把的周长分成相等的两部分?(2)、当t=时,把的面积分成相等的两部分?(3)、当t为何值时,的面积为12?26. 某中学七年级数学课外兴趣小组在探究:“边形共有多少条对角线”这一问题时,设计了如下表格,(1)、请在表格中的横线上填上相应的结果:
(1)、当t=时,把的周长分成相等的两部分?(2)、当t=时,把的面积分成相等的两部分?(3)、当t为何值时,的面积为12?26. 某中学七年级数学课外兴趣小组在探究:“边形共有多少条对角线”这一问题时,设计了如下表格,(1)、请在表格中的横线上填上相应的结果:多边形的边数
从多边形的一个顶点出发
▲
▲
多边形对角线的总条数
▲
▲
▲
(2)、应用得到的结果解决以下问题:
①求十二边形有多少条对角线?
②过多边形的一个顶点的所有对角线条数与这些对角线分多边形所得的三角形个数的和可能为吗?若能,请求出这个多边形的边数;若不能,请说明理由.