山西省临汾市侯马市2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-07-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 若 $x = 1$ 是方程 $a x + 3 x = 1$ 的解，则a的值是（）

A、 $- 2$ B、 $- 1$ C、1 D、2

查看试题解析
3. 若关于x的方程x＋k＝2x﹣1的解是负数，则k的取值范围是（）

A、k＞﹣1 B、k＜﹣1 C、k≥﹣1 D、k≤﹣1

查看试题解析
4. 小虎、大壮和明明三人玩飞镖游戏，各投5支镖，规定在同一环内得分相同，中靶和得分情况如图，则大壮的得分是（）

A、20 B、22 C、23 D、25

查看试题解析
5. 下列正多边形中，与正八边形组合能够铺满地面的是（）

A、正三角形 B、正方形 C、正五边形 D、正六边形

查看试题解析
6. 如图，桐桐从A点出发，前进3m到点B处后向右转20°，再前进3m到点C处后又向右转20°，…，这样一直走下去，她第一次回到出发点A时，一共走了（）

A、100m B、90m C、54m D、60m

查看试题解析
7. 把边长相等的正五边形 $A B C D E$ 和正方形 $A B F G$ 按照如图所示的方式叠合在一起，则 $∠ E A G$ 的度数是（　　）

A、 $18 °$ B、 $20 °$ C、 $28 °$ D、 $30 °$

查看试题解析
8. 如图，将△ABC绕点A逆时针旋转一定角度，得到△ADE．若∠CAE=65°，∠E=70°，且AD⊥BC，∠BAC的度数为（）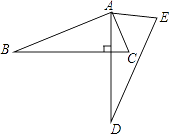

A、60° B、75° C、85° D、90°

查看试题解析
9. 轮船在河流中来往航行于A、 $B$ 两码头之间，顺流航行全程需 $7$ 小时，逆流航行全程需 $9$ 小时，已知水流速度为每小时 $3 k m$ ，求 $A$ 、 $B$ 两码头间的距离．若设A、 $B$ 两码头间距离为 $x$ ，则所列方程为（）

A、 $\frac{x}{7} + 3 = \frac{x}{9} - 3$ B、 $\frac{x}{7} - 3 = \frac{x}{9} + 3$ C、 $\frac{x}{7} + 3 = \frac{x}{9}$ D、 $\frac{x}{7} - 3 = \frac{x}{9}$

查看试题解析
10. 如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE的外面时，此时测得∠1=112°，∠A=40°，则∠2的度数为（）

A、32° B、33° C、34° D、38°

查看试题解析

二、填空题

11. 三角形三边为3，5，x，则x的范围是．

查看试题解析
12. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $B C = 4$ ，将 $Δ A B C$ 沿 $B C$ 方向平移得到 $Δ D E F$ ，若 $D E = 6$ ， $E C = 1$ ，则四边形 $A B F D$ 的周长为.

查看试题解析
13. 如图，则 $∠ A ＋ ∠ B ＋ ∠ C ＋ ∠ D ＋ ∠ E ＋ ∠ F$ 的度数为．

查看试题解析
14. 如图，将 $△ A B C$ 绕点A逆时针旋转 $90 °$ 能与 $△ A D E$ 重合点D在线段 $B C$ 的延长线上，若 $∠ B A C = 20 °$ ，则 $∠ A E D$ 的大小为．

查看试题解析
15. 如图， $∠ M O N = 30 °$ ，点 $A_{1} 、 A_{2} 、 A_{3} \dots$ 在射线 $O N$ 上，点 $B_{1} 、 B_{2} 、 B_{3} \dots$ 在射线 $O M$ 上， $△ A_{1} B_{1} A_{2} 、 △ A_{2} B_{2} A_{3} 、 △ A_{3} B_{3} A_{4} …$ 均为等边三角形，从左起第1个等边三角形的边长记为 $a_{1}$ ，第2个等边三角形的边长记为 $a_{2}$ ，以此类推，若 $O A_{1} = 1$ ，则 $a_{2023} =$ ．

查看试题解析

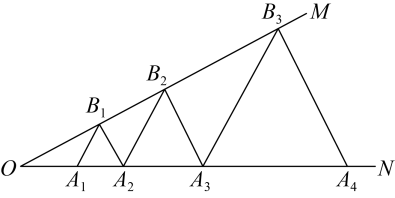
三、解答题

16.

(1)、解方程组： ${\begin{array}{l} \frac{x + 3}{2} + \frac{y + 5}{3} = 7 \\ \frac{x - 4}{3} + \frac{2 y - 3}{5} = 2 \end{array}$ ；

(2)、解不等式组： ${\begin{array}{l} x - 3 (x - 2) < 4 \\ x - 1 \leq \frac{1 + 2 x}{3} \end{array}$ ，并把解集表示在下面的数轴上．

查看试题解析
17. 如图，△ABC的顶点都在方格纸的格点上．（不写做法）

(1)、画出△ABC关于直线MN的对称图形△A₁B₁C₁；

(2)、画出△ABC关于点O的中心对称图形△A₂B₂C₂；

(3)、画出△ABC绕点B逆时针旋转90°后的图形△A₃B₃C₃；

(4)、画出△ABC先向左平移2个单位长度，再向下平移7个单位长度得到的△A₄B₄C₄ ．

查看试题解析
18. 甲、乙两人共同解方程组 ${\begin{array}{l} a x + 5 y = 15 ① \\ 4 x - b y = - 2 ② \end{array}$ ，由于甲看错了方程①中的a，得到方程组的解为 ${\begin{array}{l} x = - 3 \\ y = - 1 \end{array}$ ，乙看错了方程②中的b，得到方程组的解为 ${\begin{array}{l} x = 5 \\ y = 4 \end{array}$ ，试计算 $a^{2023} + {(- \frac{1}{10} b)}^{2024}$ 的值．

查看试题解析
19.

(1)、如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案，图案中央是一块正六边形地板砖，周围是正方形和正三角形的地板砖．从里向外第一层包括6块正方形和6块正三角形地板砖；第二层包括6块正方形和 $18$ 块正三角形地板砖；以此递推．

①第3层中分別含有块正方形和块正三角形地板砖．
②第n层中含有块正三角形地板砖（用含n的代数式表示）．

(2)、【应用】该市打算在一个新建广场中央，采用如图样式的图案铺设地面，现有1块正六边形、150块正方形地板砖，问：铺设这样的图案，还需要多少块正三角形地板砖？请说明理由．

查看试题解析
20. 已知关于x的不等式组 ${\begin{matrix} 5 x + 2 > 3 (x - 1) \\ \frac{1}{2} x \leq 8 - \frac{3}{2} x + 2 a \end{matrix}$ 有三个整数解，求实数a的取值范围．

查看试题解析
21. 如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB=50°，∠C=60°，求∠DAE和∠BOA的度数。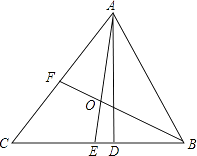

查看试题解析
22. 为改善河流水质，治污公司决定购买10台污水处理设备．现有A，B两种型号的设备，其中每台的价格，月处理污水量如下表：经调查：购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元．

A型
B型
价格（万元/台）
a
b
处理污水量（吨/月）
240
200

(1)、求a，b的值；

(2)、治污公司经预算购买污水处理设备的资金不超过105万元，你认为该公司有哪几种购买方案；

(3)、在（2）的条件下，若每月要求处理污水量不低于2040吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案．

查看试题解析
23. 问题情景：如图①，有一块直角三角板 $P M N$ 放置在 $△ A B C$ 上（ $P$ 点在 $△ A B C$ 内），三角板 $P M N$ 的两条直角边 $P M$ 、 $P N$ 恰好分别经过点 $B$ 和点 $C$ ．探究 $∠ A B P$ 与 $∠ A C P$ 是否存在某种确定的数量关系．

(1)、特殊探究：若 $∠ A = 50 °$ ，则 $∠ A B C + ∠ A C B =$ 度， $∠ P B C + ∠ P C B =$ 度， $∠ A B P + ∠ A C P =$ 度；

(2)、类比探索：请探究 $∠ A B P + ∠ A C P$ 与 $∠ A$ 的关系；

(3)、类比延伸：如图②，改变直角三角板 $P M N$ 的位置，使 $P$ 点在 $△ A B C$ 外，三角板 $P M N$ 的两条直角边 $P M$ 、 $P N$ 仍然分别经过点 $B$ 和点 $C$ ，（2）中的结论是否仍然成立？若不成立，请直接写出你的结论，并说明理由．

查看试题解析

	A型	B型
价格（万元/台）	a	b
处理污水量（吨/月）	240	200