山东省泰安市泰山区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-17 类型:期末考试
一、单选题
-
1. 若 , 则下列选项中一定成立的是( )A、 B、 C、 D、2. 下列说法中,正确的是( )A、随机事件发生的概率为 B、连续抛一枚均匀硬币次必有次正面朝上 C、概率很小的事件不可能发生 D、不可能事件发生的概率为3. 不等式组的解集,在数轴上表示正确的是( )A、
 B、
C、
B、
C、 D、
D、 4. 如果方程与下面方程中的一个组成的方程组的解为 , 那么这个方程是( )A、 B、 C、 D、5. 如图,在中,分别以 , 为圆心,大于长为半径作弧,两弧分别相交于 , 两点,作直线 , 分别交线段 , 于点 , . 若 , 的周长为 , 则的周长为( )
4. 如果方程与下面方程中的一个组成的方程组的解为 , 那么这个方程是( )A、 B、 C、 D、5. 如图,在中,分别以 , 为圆心,大于长为半径作弧,两弧分别相交于 , 两点,作直线 , 分别交线段 , 于点 , . 若 , 的周长为 , 则的周长为( )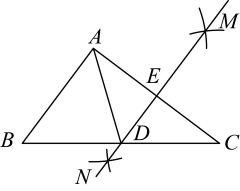 A、 B、 C、 D、6. 一副直角三角板如图放置,点在的延长线上, , , , , 则的度数为( )
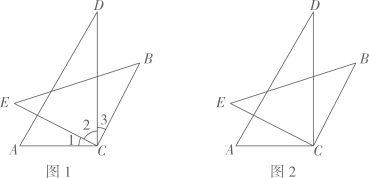
A、 B、 C、 D、6. 一副直角三角板如图放置,点在的延长线上, , , , , 则的度数为( )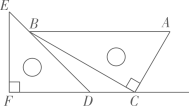 A、 B、 C、 D、7. 掷一枚质地均匀的骰子,骰子停止后,出现可能性大的是( )A、小于3的点数 B、大于3的点数 C、小于5的点数 D、大于5的点数8. 如图, , 点在边上,已知 , , 则的度数为( )
A、 B、 C、 D、7. 掷一枚质地均匀的骰子,骰子停止后,出现可能性大的是( )A、小于3的点数 B、大于3的点数 C、小于5的点数 D、大于5的点数8. 如图, , 点在边上,已知 , , 则的度数为( ) A、 B、 C、 D、9. 下列结论正确的是( )A、有两个锐角相等的两个直角三角形全等 B、两个等边三角形全等 C、一条斜边对应相等的两个直角三角形全等 D、顶角和底边对应相等的两个等腰三角形全等10. 已知是方程的解,则代数式的值为( )A、4 B、2 C、1 D、511. 把一张对边互相平行的纸条折成如图所示,是折痕,若 , 则下列结论正确:①;②;③;④ . 其中正确的个数是( )
A、 B、 C、 D、9. 下列结论正确的是( )A、有两个锐角相等的两个直角三角形全等 B、两个等边三角形全等 C、一条斜边对应相等的两个直角三角形全等 D、顶角和底边对应相等的两个等腰三角形全等10. 已知是方程的解,则代数式的值为( )A、4 B、2 C、1 D、511. 把一张对边互相平行的纸条折成如图所示,是折痕,若 , 则下列结论正确:①;②;③;④ . 其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个12. 如图,已知直线 , , , 且比大 , 那么的大小是( )
A、1个 B、2个 C、3个 D、4个12. 如图,已知直线 , , , 且比大 , 那么的大小是( )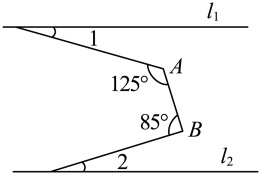 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度与右边滑梯的水平长度相等,那么判定与全等的依据是 .
 14. 已知一次函数 的图象如图,根据图中信息请写出不等式 的解集为 .
14. 已知一次函数 的图象如图,根据图中信息请写出不等式 的解集为 . 15. 《九章算术》是中国古代数学著作之一,书中有这样一个问题:五只雀、六只燕共重一斤,雀重燕轻,互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少?设一只雀的重量为 斤,一只燕的重量为 斤,则可列方程为 .16. 如图,依下列步骤尺规作图,并保留作图痕迹:
15. 《九章算术》是中国古代数学著作之一,书中有这样一个问题:五只雀、六只燕共重一斤,雀重燕轻,互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少?设一只雀的重量为 斤,一只燕的重量为 斤,则可列方程为 .16. 如图,依下列步骤尺规作图,并保留作图痕迹:
a.分别以点A,B为圆心,大于AB的长为半径作弧,两弧相交于E,F两点,作直线EF;
b.以点A为圆心,适当长为半径画弧,分别交AB,AC于点G,H,再分别以点G,H为圆心,大于GH的长为半径画弧,两弧在∠BAC的内部相交于点O,画射线AO,交直线EF于点M.已知线段AB=6,∠BAC=60°,则点M到射线AC的距离为 .
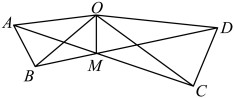
17. 已知直线 , 将一块含有角的直角三角板按如图方式放置,其中斜边与直线相交于点 , AB与直线n的交点标为点E .若 , 则的度数为 . 18. 若关于的不等式组无解,则的取值范围 .19. 若方程组有正整数解,则整数的值为 .20. 如图,在锐角中, , 、为的角平分线.且、交于点 , 连接 . 有下列四个结论:①;②;③;④ . 其中结论正确的序号是 .
18. 若关于的不等式组无解,则的取值范围 .19. 若方程组有正整数解,则整数的值为 .20. 如图,在锐角中, , 、为的角平分线.且、交于点 , 连接 . 有下列四个结论:①;②;③;④ . 其中结论正确的序号是 .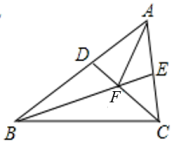
三、解答题
-
21.(1)、解不等式: , 并在数轴上表示解集.
 (2)、解不等式组 , 并写出它的整数解.22. 在甲、乙两个不透明的布袋里,都装有个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字 , , ;乙袋中的小球上分别标有数字 , , . 现从甲袋中任意摸出一个小球,记其标有的数字为 , 再从乙袋中任意摸出一个小球,记其标有的数字为 , 以此确定点的坐标 .(1)、写出点所有可能的坐标;(2)、求点在函数图像上的概率.23. 解下列方程组:(1)、;(2)、 .24. 如图,在四边形中, , 连接 , 点在边上,点在边上,且 .
(2)、解不等式组 , 并写出它的整数解.22. 在甲、乙两个不透明的布袋里,都装有个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字 , , ;乙袋中的小球上分别标有数字 , , . 现从甲袋中任意摸出一个小球,记其标有的数字为 , 再从乙袋中任意摸出一个小球,记其标有的数字为 , 以此确定点的坐标 .(1)、写出点所有可能的坐标;(2)、求点在函数图像上的概率.23. 解下列方程组:(1)、;(2)、 .24. 如图,在四边形中, , 连接 , 点在边上,点在边上,且 . (1)、求证:;(2)、若平分 , , 求的度数.25. 四月份是樱桃上市的旺季.某水果超市销售樱桃,第一周每千克樱桃的销售单价比第二周销售单价高元,该水果超市这两周共销售樱桃千克,且第一周樱桃的销量与第二周的销量之比为 , 该水果超市这两周樱桃销售总额为元.(1)、第二周樱桃销售单价是每千克多少元?(2)、随着樱桃的大量上市,四月份第三周,樱桃定价与第二周保持一致,且该水果超市推出会员优惠活动,所有的会员均可享受每千克直降元的优惠,而非会员需要按照原价购买,第三周樱桃的销量比第二周增加了 , 其中通过会员优惠活动购买的销量占第三周樱桃总销量的 , 且大于非会员的销量,求为整数的最小值.
(1)、求证:;(2)、若平分 , , 求的度数.25. 四月份是樱桃上市的旺季.某水果超市销售樱桃,第一周每千克樱桃的销售单价比第二周销售单价高元,该水果超市这两周共销售樱桃千克,且第一周樱桃的销量与第二周的销量之比为 , 该水果超市这两周樱桃销售总额为元.(1)、第二周樱桃销售单价是每千克多少元?(2)、随着樱桃的大量上市,四月份第三周,樱桃定价与第二周保持一致,且该水果超市推出会员优惠活动,所有的会员均可享受每千克直降元的优惠,而非会员需要按照原价购买,第三周樱桃的销量比第二周增加了 , 其中通过会员优惠活动购买的销量占第三周樱桃总销量的 , 且大于非会员的销量,求为整数的最小值.