山东省淄博市张店区2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-07-17 类型：期末考试

进入出卷网下载

一、单选题

1. “投掷一枚均匀的骰子，掷出的点数是6”这一事件是（）

A、随机事件 B、不可能事件 C、必然事件 D、无法确定

查看试题解析
2. 如图， $a ∥ b$ ， $∠ 1 = 50 °$ ，则∠2的度数是（）

A、 $150 °$ B、 $130 °$ C、 $50 °$ D、 $40 °$

查看试题解析
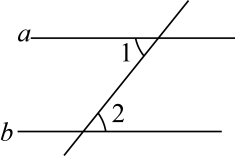3. 不等式组的解集如图所示，则该解集可以表示为（）

A、 $- 1 < x \leq 2$ B、 $- 1 < x < 2$ C、 $- 1 \leq x < 2$ D、 $- 1 \leq x \leq 2$

查看试题解析
4. 下列命题属于真命题的是（）

A、相等的角是对顶角 B、同旁内角相等，两直线平行 C、同位角相等 D、平行于同一条直线的两条直线互相平行

查看试题解析
5. 一只蜘蛛爬到如图所示的一面墙上，停留位置是随机的，则停留在阴影区域上的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
6. 若方程组 ${\begin{array}{l} 3 x - y = 6 \\ x + 2 y = - 2 \end{array}$ 的解也是关于x，y的方程 $2 x + k y = 8$ （k是常数）的解，则k的值为（）

A、3 B、1 C、 $- 1$ D、 $- 3$

查看试题解析
7. 在 $R t △ A B C$ 中， $∠ A = 90 °$ ，以C为圆心，适当长为半径画弧交 $B C$ ， $A C$ 于D，E两点，分别以D，E为圆心，大于 $\frac{1}{2} D E$ 长为半径画弧交于点M，作射线 $C M$ 交 $A B$ 于点K．以K为圆心， $C K$ 为半径画弧交射线 $C M$ 于点H，分别以C，H为圆心，大于 $\frac{1}{2} C H$ 长为半径画弧交于点N，L，作直线 $N L$ 交 $B C$ 于点G．若 $C H = 8$ ， $C G = 5$ ，则 $A K =$ （）

A、2 B、 $2.4$ C、 $2.6$ D、3

查看试题解析
8. 已知关于 $x ， y$ 的方程组 ${\begin{array}{l} x + y - b = 0 \\ 2 x + y - 3 = 0 \end{array}$ 的解是 ${\begin{array}{l} x = - 1 \\ y = m \end{array}$ ，则直线 $y = - x + b$ 与直线 $y = - 2 x + 3$ 的交点坐标是（）

A、 $(- 1 ， - 5)$ B、 $(- 1 ， 5)$ C、 $(0 ， 3)$ D、 $(5 ， - 1)$

查看试题解析
9. 若关于 $x$ 的不等式组 ${\begin{array}{l} 2 x + 3 > 5 \\ x - m \leq 0 \end{array}$ 恰有两个整数解，则实数 $m$ 的取值范围是（）

A、 $2 < m < 3$ B、 $3 < m < 4$ C、 $3 \leq m < 4$ D、 $3 < m \leq 4$

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，点 $D$ 在边 $B C$ 上，点 $E$ 在 $∠ C$ 内部，且 $△ A D E$ 是等边三角形， $∠ C B E = 60 °$ ．若 $B C = 5$ ， $B E = 3$ ，则 $△ A B D$ 的面积为（）

A、 $\frac{5 \sqrt{3}}{2}$ B、 $3 \sqrt{3}$ C、 $4 \sqrt{3}$ D、 $5 \sqrt{3}$

查看试题解析

二、填空题

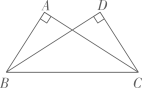
11. 把命题“对顶角相等”改写成“如果……，那么……”的形式为．

查看试题解析
12. 如图，在Rt $△$ ABC与Rt $△$ DCB中，已知∠A＝∠D＝90°，为了使Rt $△$ ABC≌Rt $△$ DCB，需添加的条件是（不添加字母和辅助线）．

查看试题解析

13. 某数学社团做排球试验：一只不透明的袋子中装有若干个红球和白球，这些球除颜色外都相同。将这个袋中的球搅匀后从中任意摸出1个球，记下颜色后放回、搅匀，不断重复这个过程，获得如下数据：

摸球次数 $n$	300	400	500	1000	1600	2000
摸到白球的次数 $m$	192	232	298	590	968	1202
摸到白球的频率 $\frac{m}{n}$	0.640	0.580	0.596	0.590	0.605	0.601

根据以上数据估计，摸到白球的概率的为（精确到0.1）．

查看试题解析

14. 如图，直线 $y_{1} = m x ， y_{2} = k x + b$ 交于点 $P (2 ， 1)$ ，则关于x的不等式 $k x + b > m x \geq - 1$ 的解集为．

查看试题解析
15. 三角板是我们数学课必备工具之一，小明同学某天上数学拓展课的时候，转动其中一个三角板发现了一个很奇妙的结论：如图，小明将含60°角的三角板 $A B C$ 绕点 $A$ 顺时针转动到 $△ A F E$ 的位置（在三角板 $A B C$ 所在的平面内转动，其中， $∠ C = 90 °$ ），当 $30 ° < ∠ C A F < 150 °$ 时，延长线段 $B C$ 和线段 $E F$ 相交于点 $D$ ，发现 $B D - D F$ 的长始终保持不变．若 $B D - D F = 4$ ，则 $A C$ 的长为．

查看试题解析

三、解答题

16. 解方程组：

(1)、 ${\begin{array}{l} 2 y - x = - 4 \\ x + y = - 5 \end{array}$

(2)、 ${\begin{array}{l} 5 (x + y) - 3 (x - y) = 16 \\ 3 (x + y) - 5 (x - y) = 0 \end{array}$

查看试题解析
17. 解不等式（组），并把解集在数轴上表示出来（自己画出数轴）．

(1)、 $2 x - 3 < \frac{x + 1}{3}$

(2)、 ${\begin{array}{l} 2 x - 13 \leq 2 - 3 x \\ 2 (x + 1) < 5 x - 2 \end{array}$

查看试题解析
18. 已知如图： $A D ∥ B C$ ， E，F分别在 $D C$ ， $A B$ 的延长线上， $∠ D C B = ∠ D A B$ ， $A E ⊥ E F$ ．

(1)、求证： $D C ∥ A B$ ；

(2)、若 $∠ D E A = 26 °$ ，求 $∠ A F E$ 的大小．

查看试题解析
19. 如图，端午节期间，某商场为了吸引顾客，设立了一个可以自由转动的转盘（转盘等分成16份），并规定顾客每购买200元商品，就能获得一次转动转盘的机会，如果转盘停止后，指针对准红，黄，绿的区域，顾客就可以分别获得50元，20元，10元的奖金，对准无色区域则无奖金．

(1)、小明购物180元，他获得奖金的概率是多少？

(2)、小芳购物210元，那么她获得奖金的概率是多少？

(3)、现商场想调整获得20元奖金的概率为 $\frac{1}{4}$ ，其他金额的获奖率不变，则需要将多少个无色区域涂上黄色？

查看试题解析
20. 如图，在 $△ A B C$ 中， $A B = 3 \sqrt{2}$ ， D是边 $A C$ 上一点， $A D = B D = 3$ ，在 $B D$ 上截取 $D F = D C$ ，连接 $A F$ 并延长交 $B C$ 于点E．

(1)、请判断 $△ A B D$ 的形状，并说明理由；

(2)、求证： $△ A D F ≌ △ B D C$ ；

(3)、若 $B E = C E$ ，请求出 $A C$ 的长．

查看试题解析
21. 为积极响应“一盔一带”安全守护行动，某商场欲购进一批头盔进行销售．已知购进8个甲型头盔和6个乙型头盔需要630元，购进6个甲型头盔和8个乙型头盔需要700元．

(1)、购进1个甲型头盔和1个乙型头盔分别需要多少元？

(2)、若该商场准备购进200个这两种型号的头盔，总费用不超过10200元，预计分别以58元/个和98元/个的价格全部销售完甲和乙两种型号的头盔，能否实现利润不少于6190元的目标？若能，请给出相应的采购方案：若不能，请说明理由．

查看试题解析
22. 如图，直线 $l_{1}$ ： $y_{1} = k x + b$ 与y轴交于点A，与x轴交于点 $B (\frac{3}{2} ， 0)$ ，直线 $l_{2}$ ： $y_{2} = - \frac{1}{2} x + 2$ 与y轴交于点C，与直线 $l_{1}$ 交于点D，点D到y轴的距离为2．

(1)、求直线 $l_{1}$ 的函数表达式；

(2)、请直接写出方程组 ${\begin{array}{l} k x - y = - b \\ x + 2 y = 4 \end{array}$ 的解：；

(3)、求 $△ A C D$ 的面积；

(4)、在直线 $l_{1}$ 上是否存在异于点D的另一点M，使得 $△ A C D$ 与 $△ A C M$ 的面积相等？若存在，请求出点M的坐标；若不存在，请说明理由．

查看试题解析
23. 已知线段 $A B$ 垂直直线 $l$ 于点 $B$ ，点 $D$ 在直线 $l$ 上，分别以 $A B$ ， $A D$ 为边作等边三角形 $A B C$ （点 $C$ 在边 $A B$ 的右侧）和等边三角形 $A D E$ ，直线 $C E$ 交直线 $l$ 于点 $F$ ．

(1)、当点 $F$ 在线段 $B D$ 上时，如图1，求证： $C E = C F + D F$ ；

(2)、①当点 $F$ 在线段 $B D$ 的延长线上时（如图2），请直接写出线段 $C E$ ， $C F$ ， $D F$ 之间的数量关系；
②当点 $F$ 在线段 $D B$ 的延长线上时（如图3），请直接写出线段 $C E$ ， $C F$ ， $D F$ 之间的数量关系；
③在①和②中，选择其中一个进行证明；

(3)、当 $B D = 3 B F$ ，且 $E F = 16$ 时，请直接写出 $A B$ 的长．

查看试题解析