上海市嘉定区2022--2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-17 类型:期末考试
一、单选题
-
1. 在中,无理数个数有( )A、1个 B、2个 C、3个 D、4个2. 下列运算中,正确的是( )A、 B、 C、 D、3. 如果一个三角形的两边长分别为3和7,则第三边长可能是( ).A、3 B、4 C、7 D、104. 如图,用直尺和圆规作出的角平分线 , 在作角平分线过程中,用到的三角形全等的判定方法是( )
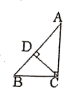
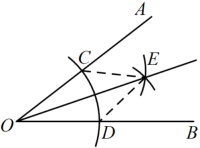 A、 B、 C、 D、5. 如右图,在 中, , ,垂足为点 ,有下列说法:①点 与点 的距离是线段 的长;②点 到直线 的距离是线段 的长;③线段 是 边 上的高;④线段 是 边 上的高.
A、 B、 C、 D、5. 如右图,在 中, , ,垂足为点 ,有下列说法:①点 与点 的距离是线段 的长;②点 到直线 的距离是线段 的长;③线段 是 边 上的高;④线段 是 边 上的高.上述说法中,正确的个数为( )
 A、1个 B、2个 C、3个 D、4个6. 如图,在△ABC中,点D、E分别在边AB、AC上,BE与CD相交于点O,如果已知∠ABC=∠ACB,那么还不能判定△ABE≌△ACD,补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
A、1个 B、2个 C、3个 D、4个6. 如图,在△ABC中,点D、E分别在边AB、AC上,BE与CD相交于点O,如果已知∠ABC=∠ACB,那么还不能判定△ABE≌△ACD,补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )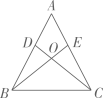 A、AD=AE B、BE=CD C、OB=OC D、∠BDC=∠CEB
A、AD=AE B、BE=CD C、OB=OC D、∠BDC=∠CEB二、填空题
-
7. 的平方根是 .8. 化成幂的形式.9. 比较大小:-4 (填“>”、“=”或“<”).10. 如果等腰三角形两边长是和 , 那么它的周长是 .11. 将24870000这个数保留两个有效数字并用科学记数法表示是 .12. 已知在两个连续整数a和b之间(a<b),那么ab= .13. 若点P(3,m-2)在x轴上,则点Q(m-3,m+1)在第象限.14. 已知一个等腰三角形,其中一条腰上的高与另一条腰的夹角为25°,则该等腰三角形的顶角为 .15. 如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=24°,则∠BDC=度.
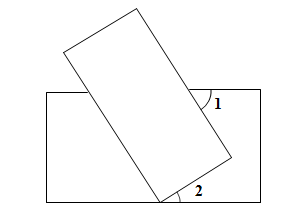
 16. 如图,将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1+∠2=°.
16. 如图,将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,则∠1+∠2=°.
 17. 如图,∥ , 点A、E在直线上,点B、C、D在直线上,如果BD:CD=2:1,△ABC的面积为30,那么△BDE的面积是 .
17. 如图,∥ , 点A、E在直线上,点B、C、D在直线上,如果BD:CD=2:1,△ABC的面积为30,那么△BDE的面积是 .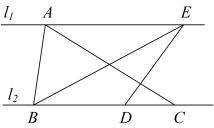 18. 如图,已知△ABC≌△ADE,且点B与点D对应,点C与点E对应,点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是°.
18. 如图,已知△ABC≌△ADE,且点B与点D对应,点C与点E对应,点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是°.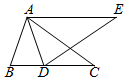
三、解答题
-
19. 计算: .20. 计算: .21. 计算: .22. 用幂的运算性质计算:23. 如图,已知 , , , 请说明的理由.
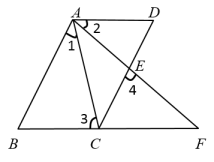
解:因为(已知)
所以( )
因为(已知)
所以( )
因为(已知)
所以( )
即 ▲ .
所以 ▲ .(等量代换)
因此( )
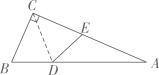
24. 阅读、填空并将说理过程补充完整:如图,已知点D、E分别在△ABC的边AB、AC上,且∠AED=∠B,延长DE与BC的延长线交于点F,∠BAC和∠BFD的角平分线交于点G.那么AG与FG的位置关系如何?为什么?解:AG⊥FG.将AG、DF的交点记为点P,延长AG交BC于点Q.
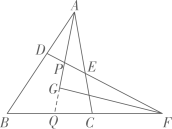
因为AG、FG分别平分∠BAC和∠BFD(已知)
所以∠BAG= ▲ , ▲ (角平分线定义)
又因为∠FPQ= ▲ +∠AED, ▲ = ▲ +∠B
(三角形的一个外角等于与它不相邻的两个内角的和)
∠AED=∠B(已知)
所以∠FPQ= ▲ (等式性质)
(请完成以下说理过程)
25. 如图,在直角坐标平面内,已知点A的坐标是(0,4). (1)、图中B点的坐标是 .(2)、点B关于原点对称的点C的坐标是;点A关于x轴对称的点D的坐标是 .(3)、的面积是 .(4)、如果点E在x轴上,且 , 那么点E的坐标是 .26. 在中, , 以为边向外作等边和等边 .
(1)、图中B点的坐标是 .(2)、点B关于原点对称的点C的坐标是;点A关于x轴对称的点D的坐标是 .(3)、的面积是 .(4)、如果点E在x轴上,且 , 那么点E的坐标是 .26. 在中, , 以为边向外作等边和等边 . (1)、如图1,连接 , 与相交于点O.
(1)、如图1,连接 , 与相交于点O.①说明的理由 .
②°.(直接填答案)
(2)、如图2,过D做的垂线 , 垂足为H,连接 , 交于点F,与相等吗?为什么?27. 在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°). (1)、∠ABO的度数为°,△AOB . (填“是”或“不是”)“灵动三角形”;(2)、若∠BAC=70°,则△AOC(填“是”或“不是”)“灵动三角形”;(3)、当△ABC为“灵动三角形”时,求∠OAC的度数.
(1)、∠ABO的度数为°,△AOB . (填“是”或“不是”)“灵动三角形”;(2)、若∠BAC=70°,则△AOC(填“是”或“不是”)“灵动三角形”;(3)、当△ABC为“灵动三角形”时,求∠OAC的度数.