上海市普陀区2022-2023年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-17 类型:期末考试
一、单选题
-
1. 下列实数中,无理数是( )A、0 B、 C、 D、2. 下列说法中,错误的是( )A、1的平方根是1 B、0的任何次方根都是0 C、的立方根是 D、负数没有平方根3. 如图,已知在和中, , , 能直接判定的依据是( )
 A、 B、 C、 D、4. 在直角坐标平面内,如果点在第二象限,那么点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列说法:①同旁内角互补;②对顶角相等;③三角形的一个外角大于任何一个内角;④如果三条线段、、满足 , 那么这三条线段、、一定能组成三角形.其中正确的个数是( )A、1个 B、2个 C、3个 D、4个6. 在直角坐标平面内,经过平移,其顶点 的对应点的坐标是 , 那么其内部任意一点的对应点的坐标一定是( )A、 B、 C、 D、
A、 B、 C、 D、4. 在直角坐标平面内,如果点在第二象限,那么点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列说法:①同旁内角互补;②对顶角相等;③三角形的一个外角大于任何一个内角;④如果三条线段、、满足 , 那么这三条线段、、一定能组成三角形.其中正确的个数是( )A、1个 B、2个 C、3个 D、4个6. 在直角坐标平面内,经过平移,其顶点 的对应点的坐标是 , 那么其内部任意一点的对应点的坐标一定是( )A、 B、 C、 D、二、填空题
-
7. 36的平方根是.8. 计算:( )2=。9. 比较大小: . (填“”,“”或“”)10. 用科学记数法表示 , 结果保留两个有效数字约为 .11. 在直角坐标平面内,点A的坐标为 , 点B的坐标为 , 那么A、B两点间的距离等于 .12. 如图,已知直线 , 点A在直线a上,点B、C在直线b上,点P在线段上,如果 , , 那么 .
 13. 在平面直角坐标系内,点关于y轴对称的点的坐标为 .14. 经过点Q (2,﹣3)且平行y轴的直线可以表示为直线 .15. 如图,在中,点是角平分线的交点,若 , .
13. 在平面直角坐标系内,点关于y轴对称的点的坐标为 .14. 经过点Q (2,﹣3)且平行y轴的直线可以表示为直线 .15. 如图,在中,点是角平分线的交点,若 , . 16. 如果一个等腰三角形的周长等于20,且一边的长等于4,那么这个等腰三角形的腰长等于 .17. 如图,在中, , 点D、E分别在边、上, , 如果 , , 那么 .
16. 如果一个等腰三角形的周长等于20,且一边的长等于4,那么这个等腰三角形的腰长等于 .17. 如图,在中, , 点D、E分别在边、上, , 如果 , , 那么 . 18. 在中, , 点D是边上的一点,将沿直线翻折,使点B落在边上的点E处,如果是等腰三角形,那么 .
18. 在中, , 点D是边上的一点,将沿直线翻折,使点B落在边上的点E处,如果是等腰三角形,那么 .三、解答题
-
19. 计算:20. 计算: . (结果用幂的形式表示).21. 已知:如图,在中,点D、G分别在边、上,且 , F在的延长线上,E在上,如果 , 说明的理由.
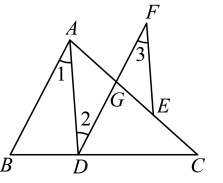
解:因为(已知),所以( )
所以 ▲ ( ).
因为 ▲ (三角形的一个外角等于与它不相邻的两个内角的和).
因为(已知),所以 ▲ (等式性质).
所以(等量代换).
22. 如图,在中, , 点D、E在边上(点D在点E的左侧), , , 说明是等边三角形的理由.
解:因为(已知),所以( ).
在和中, .
所以 ▲ (全等三角形的对应边相等),(全等三角形的对应角相等).
因为( ),
又因为(已知),
所以 . 即 .
因为(已知),所以 ▲ .
所以是等边三角形( ).
23. 根据下列要求画图并回答问题:(1)、画图(不要求写画法和结论);①画 , 使 , , ;
②分别画、边上的高、;
(2)、在(1)的图形中,可得的值为 .24. 小明已经会用三角尺过直线外一点作已知直线的垂线,小明发现如果利用直尺和圆规,也可以实现.如图7,已知直线a,点P为直线a外一点,以下是小明的作图方法:①以点P为圆心,大于点P到直线a的距离的长为半径作弧,交直线a于点A、B;
②分别以点A、点B为圆心,大于的长为半径作弧,两弧交于直线a下方一点;
③作直线 , 交直线a于点C.

试说明的理由:
解:连接、、、 .
在与中, ,
所以( ).(完成以下说理过程)
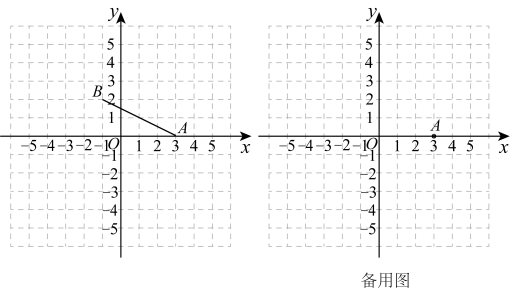
25. 如图,已知的顶点为 , 点B在轴的负半轴上且到轴的距离为5,点C与点A关于原点对称. (1)、写出点B、C的坐标是:B , C;(2)、在平面直角坐标系中画出 , 可以求得的面积是;(3)、如果点D在轴上,且 , 那么点D的坐标是 .
(1)、写出点B、C的坐标是:B , C;(2)、在平面直角坐标系中画出 , 可以求得的面积是;(3)、如果点D在轴上,且 , 那么点D的坐标是 .