湖南省长沙市2023年中考数学试卷
试卷更新日期:2023-07-17 类型:中考真卷
一、单选题
-
1. 下列各数中,是无理数的是( )A、 B、π C、 D、02. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 下列长度的三条线段,能组成三角形的是( )A、1,3,4 B、2,2,7 C、4,5,7 D、3,3,65. 2022年,长沙市全年地区生产总值约为1400000000000元,比上年增长 . 其中数据1400000000000用科学记数法表示为( )A、 B、 C、 D、6. 如图,直线直线n,点A在直线n上,点B在直线m上,连接 , 过点A作 , 交直线m于点C.若 , 则的度数为( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 下列长度的三条线段,能组成三角形的是( )A、1,3,4 B、2,2,7 C、4,5,7 D、3,3,65. 2022年,长沙市全年地区生产总值约为1400000000000元,比上年增长 . 其中数据1400000000000用科学记数法表示为( )A、 B、 C、 D、6. 如图,直线直线n,点A在直线n上,点B在直线m上,连接 , 过点A作 , 交直线m于点C.若 , 则的度数为( )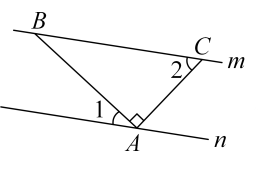 A、 B、 C、 D、7. 长沙市某一周内每日最高气温的情况如图所示,下列说法中错误的是( )
A、 B、 C、 D、7. 长沙市某一周内每日最高气温的情况如图所示,下列说法中错误的是( )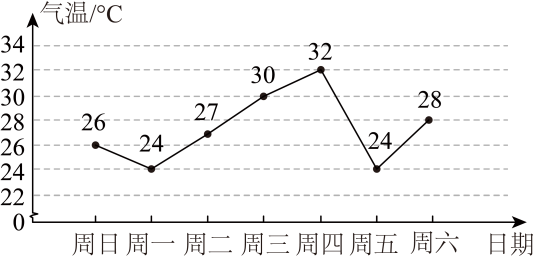 A、这周最高气温是32℃ B、这组数据的中位数是30 C、这组数据的众数是24 D、周四与周五的最高气温相差8℃8. 不等式组的解集在数轴上表示正确的是( )A、
A、这周最高气温是32℃ B、这组数据的中位数是30 C、这组数据的众数是24 D、周四与周五的最高气温相差8℃8. 不等式组的解集在数轴上表示正确的是( )A、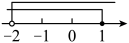 B、
B、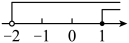 C、
C、 D、
D、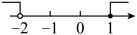 9. 下列一次函数中,y随x的增大而减小的函数是( )A、 B、 C、 D、10. “千门万户曈曈日,总把新桃换旧符”.春节是中华民族的传统节日,古人常用写“桃符”的方式来祈福避祸,而现在,人们常用贴“福”字、贴春联、挂灯笼等方式来表达对新年的美好祝愿.某商家在春节期间开展商品促销活动,顾客凡购物金额满100元,就可以从“福”字、春联、灯笼这三类礼品中免费领取一件.礼品领取规则:顾客每次从装有大小、形状、质地都相同的三张卡片(分别写有“福”字、春联、灯笼)的不透明袋子中,随机摸出一张卡片,然后领取一件与卡片上文字所对应的礼品,现有2名顾客都只领取了一件礼品,那么他们恰好领取同一类礼品的概率是( )A、 B、 C、 D、
9. 下列一次函数中,y随x的增大而减小的函数是( )A、 B、 C、 D、10. “千门万户曈曈日,总把新桃换旧符”.春节是中华民族的传统节日,古人常用写“桃符”的方式来祈福避祸,而现在,人们常用贴“福”字、贴春联、挂灯笼等方式来表达对新年的美好祝愿.某商家在春节期间开展商品促销活动,顾客凡购物金额满100元,就可以从“福”字、春联、灯笼这三类礼品中免费领取一件.礼品领取规则:顾客每次从装有大小、形状、质地都相同的三张卡片(分别写有“福”字、春联、灯笼)的不透明袋子中,随机摸出一张卡片,然后领取一件与卡片上文字所对应的礼品,现有2名顾客都只领取了一件礼品,那么他们恰好领取同一类礼品的概率是( )A、 B、 C、 D、二、填空题
-
11. 分解因式:n2﹣100= .12. 睡眠管理作为“五项管理”中重要的内容之一,也是学校教育重点关注的内容.某老师了解到班上某位学生的5天睡眠时间(单位:小时)如下:10,9,10,8,8,则该学生这5天的平均睡眠时间是 小时.13. 如图,已知 , 点D在上,以点B为圆心,长为半径画弧,交于点E,连接 , 则的度数是 度.
 14. 如图,在平面直角坐标系中,点在反比例函数为常数, , 的图象上,过点作轴的垂线,垂足为 , 连接 . 若的面积为 , 则 .
14. 如图,在平面直角坐标系中,点在反比例函数为常数, , 的图象上,过点作轴的垂线,垂足为 , 连接 . 若的面积为 , 则 .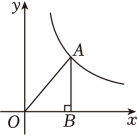 15. 如图,点A,B,C在半径为2的上, , , 垂足为E,交于点D,连接 , 则的长度为 .
15. 如图,点A,B,C在半径为2的上, , , 垂足为E,交于点D,连接 , 则的长度为 .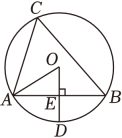 16. 毛主席在《七律二首•送瘟神》中写道“坐地日行八万里,巡天遥看一千河”,我们把地球赤道看成一个圆,这个圆的周长大约为“八万里”.对宇宙千百年来的探索与追问,是中华民族矢志不渝的航天梦想.从古代诗人屈原发出的《天问》,到如今我国首次火星探测任务被命名为“天问一号”,太空探索无上境,伟大梦想不止步.2021年5月15日,我国成功实现火星着陆.科学家已经探明火星的半径大约是地球半径的 , 若把经过火星球心的截面看成是圆形的,则该圆的周长大约为 万里.
16. 毛主席在《七律二首•送瘟神》中写道“坐地日行八万里,巡天遥看一千河”,我们把地球赤道看成一个圆,这个圆的周长大约为“八万里”.对宇宙千百年来的探索与追问,是中华民族矢志不渝的航天梦想.从古代诗人屈原发出的《天问》,到如今我国首次火星探测任务被命名为“天问一号”,太空探索无上境,伟大梦想不止步.2021年5月15日,我国成功实现火星着陆.科学家已经探明火星的半径大约是地球半径的 , 若把经过火星球心的截面看成是圆形的,则该圆的周长大约为 万里.三、解答题
-
17. 计算: .18. 先化简,再求值: , 其中 .19. 年月日点分,“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射,成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图,在发射的过程中,飞船从地面处发射,当飞船到达点时,从位于地面处的雷达站测得的距离是 , 仰角为;后飞船到达处,此时测得仰角为 .
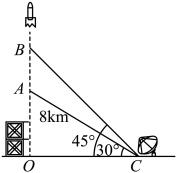 (1)、求点离地面的高度;(2)、求飞船从处到处的平均速度.(结果精确到 , 参考数据:)20. 为增强学生安全意识,某校举行了一次全校3000名学生参加的安全知识竞赛.从中随机抽取n名学生的竞赛成绩进行了分析,把成绩分成四个等级(D:;C:;B:;A:),并根据分析结果绘制了不完整的频数分布直方图和扇形统计图.
(1)、求点离地面的高度;(2)、求飞船从处到处的平均速度.(结果精确到 , 参考数据:)20. 为增强学生安全意识,某校举行了一次全校3000名学生参加的安全知识竞赛.从中随机抽取n名学生的竞赛成绩进行了分析,把成绩分成四个等级(D:;C:;B:;A:),并根据分析结果绘制了不完整的频数分布直方图和扇形统计图.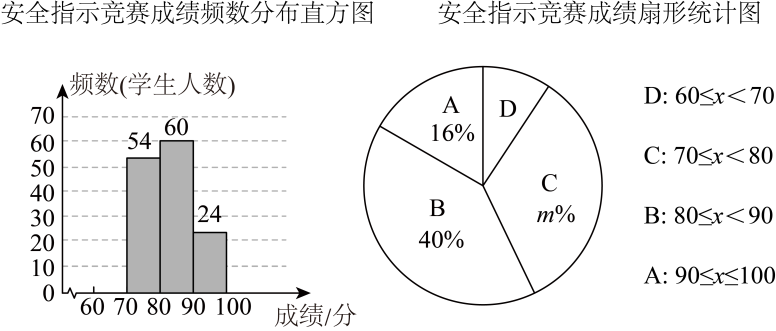
请根据以上信息,解答下列问题:
(1)、填空:n= , m=;(2)、请补全频数分布直方图;(3)、扇形统计图中B等级所在扇形的圆心角度数为 度;(4)、若把A等级定为“优秀”等级,请你估计该校参加竞赛的3000名学生中达到“优秀”等级的学生人数.21. 如图, , , , 垂足分别为 , .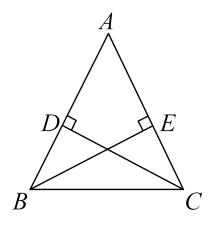 (1)、求证:;(2)、若 , , 求的长.22. 为提升学生身体素质,落实教育部门“在校学生每天锻炼时间不少于1小时”的文件精神.某校利用课后服务时间,在八年级开展“体育赋能,助力成长”班级篮球赛,共个班级参加.(1)、比赛积分规定:每场比赛都要分出胜负,胜一场积分,负一场积分.某班级在场比赛中获得总积分为分,问该班级胜负场数分别是多少?(2)、投篮得分规则:在分线外投篮,投中一球可得分,在分线内含分线投篮,投中一球可得分,某班级在其中一场比赛中,共投中个球只有分球和分球 , 所得总分不少于分,问该班级这场比赛中至少投中了多少个分球?23. 如图,在中,平分 , 交于点E,交的延长线于点F.
(1)、求证:;(2)、若 , , 求的长.22. 为提升学生身体素质,落实教育部门“在校学生每天锻炼时间不少于1小时”的文件精神.某校利用课后服务时间,在八年级开展“体育赋能,助力成长”班级篮球赛,共个班级参加.(1)、比赛积分规定:每场比赛都要分出胜负,胜一场积分,负一场积分.某班级在场比赛中获得总积分为分,问该班级胜负场数分别是多少?(2)、投篮得分规则:在分线外投篮,投中一球可得分,在分线内含分线投篮,投中一球可得分,某班级在其中一场比赛中,共投中个球只有分球和分球 , 所得总分不少于分,问该班级这场比赛中至少投中了多少个分球?23. 如图,在中,平分 , 交于点E,交的延长线于点F.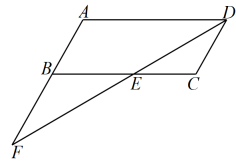 (1)、求证:;(2)、若 , 求的长和的面积.24. 如图,点A,B,C在上运动,满足 , 延长至点D,使得 , 点E是弦上一动点(不与点A,C重合),过点E作弦的垂线,交于点F,交的延长线于点N,交于点M(点M在劣弧上).
(1)、求证:;(2)、若 , 求的长和的面积.24. 如图,点A,B,C在上运动,满足 , 延长至点D,使得 , 点E是弦上一动点(不与点A,C重合),过点E作弦的垂线,交于点F,交的延长线于点N,交于点M(点M在劣弧上).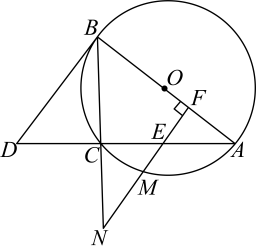 (1)、是的切线吗?请作出你的判断并给出证明;(2)、记的面积分别为 , 若 , 求的值;(3)、若的半径为1,设 , , 试求y关于x的函数解析式,并写出自变量x的取值范围.25. 我们约定:若关于x的二次函数与同时满足 , 则称函数与函数互为“美美与共”函数.根据该约定,解答下列问题:(1)、若关于x的二次函数与互为“美美与共”函数,求k,m,n的值;(2)、对于任意非零实数r,s,点与点始终在关于x的函数的图像上运动,函数与互为“美美与共”函数.
(1)、是的切线吗?请作出你的判断并给出证明;(2)、记的面积分别为 , 若 , 求的值;(3)、若的半径为1,设 , , 试求y关于x的函数解析式,并写出自变量x的取值范围.25. 我们约定:若关于x的二次函数与同时满足 , 则称函数与函数互为“美美与共”函数.根据该约定,解答下列问题:(1)、若关于x的二次函数与互为“美美与共”函数,求k,m,n的值;(2)、对于任意非零实数r,s,点与点始终在关于x的函数的图像上运动,函数与互为“美美与共”函数.①求函数的图像的对称轴;
②函数的图像是否经过某两个定点?若经过某两个定点,求出这两个定点的坐标;否则,请说明理由;
(3)、在同一平面直角坐标系中,若关于x的二次函数与它的“美美与共”函数的图像顶点分别为点A,点B,函数的图像与x轴交于不同两点C,D,函数的图像与x轴交于不同两点E,F.当时,以A,B,C,D为顶点的四边形能否为正方形?若能,求出该正方形面积的取值范围;若不请说明理由.