北师大版数学九年级上册同步练习——第二章《一元二次方程》6 应用一元二次方程(1)
试卷更新日期:2023-07-17 类型:同步测试
一、选择题
-
1. 如图,某景区内有一块长方形油菜花田地(单位:m),现在其中修建观花道(阴影部分)供游人赏花,要求观花道面积是30.设观花道的直角边为x,则可列方程为( )
 A、(10+x)(9+x)=30 B、(10+x)(9+x)=60 C、(10-x)(9-x)=30 D、(10-x)(9-x)=602. 为加快推动城市生态建设的步伐,形成“城在林中、园在城中、山水相依,林路相随”的生态格局,昆明市政府计划在某公园的一块矩形空地上修建草坪,如图,矩形长为 , 宽为 , 在矩形内的四周修筑同样宽的道路,余下的铺上草坪.要使草坪的面积为 , 道路的宽度应为多少?设矩形地块四周道路的宽度为 , 根据题意,下列方程正确的是( )
A、(10+x)(9+x)=30 B、(10+x)(9+x)=60 C、(10-x)(9-x)=30 D、(10-x)(9-x)=602. 为加快推动城市生态建设的步伐,形成“城在林中、园在城中、山水相依,林路相随”的生态格局,昆明市政府计划在某公园的一块矩形空地上修建草坪,如图,矩形长为 , 宽为 , 在矩形内的四周修筑同样宽的道路,余下的铺上草坪.要使草坪的面积为 , 道路的宽度应为多少?设矩形地块四周道路的宽度为 , 根据题意,下列方程正确的是( )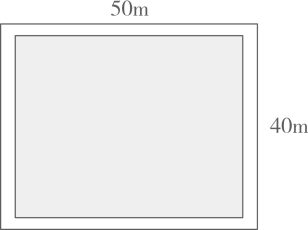 A、 B、 C、 D、3. 某超市一月份的营业额为300万元,第一季度的营业额共1200万元,如果平均每月增长率为 , 则由题意可列方程为( )A、 B、 C、 D、4. 根据福建省统计局数据,福建省2020年的地区生产总值为43903.89亿元,2022年的地区生产总值为53109.85亿元.设这两年福建省地区生产总值的年平均增长率为x,根据题意可列方程( )A、 B、 C、 D、5. 如图,某小区规划在一个长、宽的长方形场地上修建三条同样宽的通道,使其中两条与平行,另一条与平行,其余部分种花草.要使每一块草坪的面积都为 , 那么通道的宽应该满足的方程为( )
A、 B、 C、 D、3. 某超市一月份的营业额为300万元,第一季度的营业额共1200万元,如果平均每月增长率为 , 则由题意可列方程为( )A、 B、 C、 D、4. 根据福建省统计局数据,福建省2020年的地区生产总值为43903.89亿元,2022年的地区生产总值为53109.85亿元.设这两年福建省地区生产总值的年平均增长率为x,根据题意可列方程( )A、 B、 C、 D、5. 如图,某小区规划在一个长、宽的长方形场地上修建三条同样宽的通道,使其中两条与平行,另一条与平行,其余部分种花草.要使每一块草坪的面积都为 , 那么通道的宽应该满足的方程为( ) A、 B、 C、 D、6. 如图,面积为的长方形试验田一面靠墙墙的长度不限 , 另外三面用长的篱笆围成,平行于墙的一边开有一扇宽的门门的材料另计设试验田垂直于墙的一边的长为 , 则所列方程正确的是( )
A、 B、 C、 D、6. 如图,面积为的长方形试验田一面靠墙墙的长度不限 , 另外三面用长的篱笆围成,平行于墙的一边开有一扇宽的门门的材料另计设试验田垂直于墙的一边的长为 , 则所列方程正确的是( ) A、 B、 C、 D、7. 春意复苏,郑州绿化工程正在如火如荼地进行着,某工程队计划将一块长64m,宽40m的矩形场地建设成绿化广场如图,广场内部修建三条宽相等的小路,其余区域进行绿化.若使绿化区域的面积为广场总面积的80%,求小路的宽,设小路的宽为x m,则可列方程( )
A、 B、 C、 D、7. 春意复苏,郑州绿化工程正在如火如荼地进行着,某工程队计划将一块长64m,宽40m的矩形场地建设成绿化广场如图,广场内部修建三条宽相等的小路,其余区域进行绿化.若使绿化区域的面积为广场总面积的80%,求小路的宽,设小路的宽为x m,则可列方程( )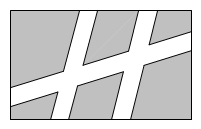 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 某校截止到年底,校园绿化面积为平方米.为美化环境,该校计划年底绿化面积达到平方米.利用方程想想,设这两年绿化面积的年平均增长率为 , 则依题意列方程为 .9. 为了加快数字化城市建设,某市计划新建一批智能充电桩,第一个月新建了301个充电桩,第三个月新建了500个充电桩,设该市新建智能充电桩个数的月平均增长率为 , 根据题意,请列出方程 .10. 《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百九十一步,只云长阔共六十步,问长多阔几何”.意思是:一块矩形田地的面积为891平方步,只知道它的长与宽共60步,问它的长比宽多多少步?根据题意得,长比宽多步.11. 如图,用一面足够长的墙为一边,其余三边用总长34米的围栏建两个面积相同的生态园,两个生态园各留一扇宽为1米的门.由于场地限制,垂直于墙的一边长不超过6米(围栏宽忽略不计).每个生态园的面积为48平方米,则每个生态园垂直于墙的一边长为 .
 12. 有一个正方形的花园,如果它的边长增加 , 那么花园面积将增加 , 则原花园的面积为 .
12. 有一个正方形的花园,如果它的边长增加 , 那么花园面积将增加 , 则原花园的面积为 .三、解答题
-
13. 如图,某小区矩形绿地的长宽分别为30m,20m.现计划对其进行扩充,将绿地的长、宽增加相同的长度后,得到一个新的矩形绿地.若扩充后的矩形绿地面积为 , 求新的矩形绿地的长与宽.
 14. 根据以下信息,探索完成任务.
14. 根据以下信息,探索完成任务.如何设计种植方案?
素材1
小明以“种植农作物”为主题在自己家100平方米的土地上进行课外实践,现有A、B两种作物的相关信息如下表所示:
A作物
B作物
每平方米种植株树(株)
2
10
单株产量(千克)
1.2
0.5
素材2
由于A作物植株间距较大,可增加A作物每平方米的种植株树.经过调研发现,每平方米种植A作物每增加1株,A作物的单株产量减少0.1千克.
素材3
若同时种植A、B两种作物,实行分区域种植.
问题解决
单一种植(全部种植A作物)
任务1:明确数量关系
设每平方米增加x株A作物(x 为正整数),则每平方米有 ▲ 株,单株产量为 ▲ 千克.(用含x的代数式表示)
任务2:计算产量
要使A作物每平方米产量为4.8千克,则每平方米应种植多少株?
单一种植(全部种植A作物)
任务3:规划种植方案
设这100平方米的土地中有a平方米用于种植A作物,且每平方米产量最大,其余区域按照每平方米10株种植B作物,当这100平方米总产量不低于496千克时,则a的取值范围是 ▲
15. 如图,物业公司计划整理出一块矩形绿地,为充分利用现有资源,该矩形绿地一面靠墙(墙的长度为),另外三面用栅栏围成,已知栅栏总长度为 , 若矩形绿地的面积为 , 求矩形垂直于墙的一边,即的长. 16. 如图,在矩形ABCD中, , . 点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6).那么当t为何值时,的面积等于8?
16. 如图,在矩形ABCD中, , . 点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6).那么当t为何值时,的面积等于8? 17. 随旅游旺季的到来,某景区游客人数逐月增加,2月份游客人数为1.6万人,4月份游客人数为2.5万人.(1)、求这两个月中该景区游客人数的月平均增长率;(2)、预计5月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.已知该景区5月1日至5月21日已接待游客2.125万人,则5月份后10天日均接待游客人数最多是多少万人?18. 如图 , 用篱笆靠墙围成矩形花圃 , 一面利用旧墙,其余三面用篱笆围,墙可利用的最大长度为 , 篱笆长为 , 设平行于墙的边长为 .
17. 随旅游旺季的到来,某景区游客人数逐月增加,2月份游客人数为1.6万人,4月份游客人数为2.5万人.(1)、求这两个月中该景区游客人数的月平均增长率;(2)、预计5月份该景区游客人数会继续增长,但增长率不会超过前两个月的月平均增长率.已知该景区5月1日至5月21日已接待游客2.125万人,则5月份后10天日均接待游客人数最多是多少万人?18. 如图 , 用篱笆靠墙围成矩形花圃 , 一面利用旧墙,其余三面用篱笆围,墙可利用的最大长度为 , 篱笆长为 , 设平行于墙的边长为 .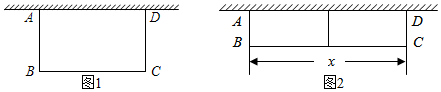 (1)、若围成的花圃面积为时,求的长;(2)、如图 , 若计划在花圃中间用一道篱笆隔成两个小矩形,且花圃面积为 , 请你判断能否围成花圃,如果能,求的长;如果不能,请说明理由.19. 如图,在矩形中, , , 动点P、Q分别以 , 的速度从点A , C同时出发,沿规定路线移动.
(1)、若围成的花圃面积为时,求的长;(2)、如图 , 若计划在花圃中间用一道篱笆隔成两个小矩形,且花圃面积为 , 请你判断能否围成花圃,如果能,求的长;如果不能,请说明理由.19. 如图,在矩形中, , , 动点P、Q分别以 , 的速度从点A , C同时出发,沿规定路线移动.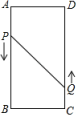
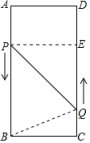 (1)、若点P从点A移动到点B停止,点Q随点P的停止而停止移动,问经过多长时间P , Q两点之间的距离是?(2)、若点P沿着移动,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间的面积为?
(1)、若点P从点A移动到点B停止,点Q随点P的停止而停止移动,问经过多长时间P , Q两点之间的距离是?(2)、若点P沿着移动,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间的面积为?