(人教版)2023-2024学年九年级数学上册22.3 实际问题与二次函数 同步分层训练(培优卷)
试卷更新日期:2023-07-16 类型:同步测试
一、选择题
-
1. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
 A、
A、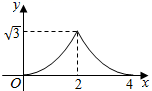 B、
B、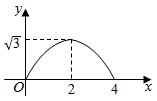 C、
C、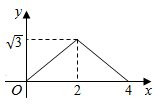 D、
D、 2. 如图,正三角形ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止.设运动时间为x(秒),y=PC2 , 则y关于x的函数的图象大致是( )
2. 如图,正三角形ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止.设运动时间为x(秒),y=PC2 , 则y关于x的函数的图象大致是( )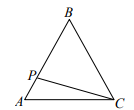 A、
A、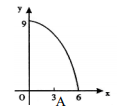 B、
B、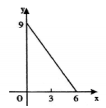 C、
C、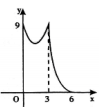 D、
D、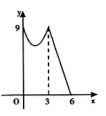 3. 如图,正方形 边长为4个单位,两动点 、 分别从点 、 处,以1单位/ 、2单位/ 的速度逆时针沿边移动.记移动的时间为 , 面积为 (平方单位),当点 移动一周又回到点 终止,同时 点也停止运动,则 与 的函数关系图象为( )
3. 如图,正方形 边长为4个单位,两动点 、 分别从点 、 处,以1单位/ 、2单位/ 的速度逆时针沿边移动.记移动的时间为 , 面积为 (平方单位),当点 移动一周又回到点 终止,同时 点也停止运动,则 与 的函数关系图象为( )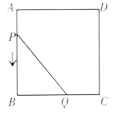 A、
A、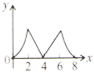 B、
B、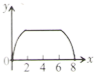 C、
C、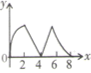 D、
D、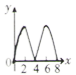 4. 已知菱形ABCD的边长为1,∠DAB=60°,E为AD上的动点,F在CD上,且AE+CF=1,设ΔBEF的面积为y,AE=x,当点E运动时,能正确描述y与x关系的图像是:( )
4. 已知菱形ABCD的边长为1,∠DAB=60°,E为AD上的动点,F在CD上,且AE+CF=1,设ΔBEF的面积为y,AE=x,当点E运动时,能正确描述y与x关系的图像是:( )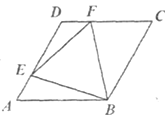 A、
A、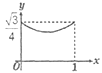 B、
B、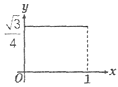 C、
C、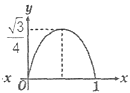 D、
D、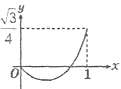 5. 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
5. 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )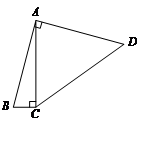
A、 B、 C、 D、6. 已知抛物线 与 轴的交点为A(1,0)和B(3,0),点P1( , ),P2( , )是抛物线上不同于A,B的两个点,记△P1AB的面积为S1 , △P2AB的面积为S2。有下列结论:①当 时,S1>S2;②当 时,S1<S2;③当 时,S1>S2;④当 时,S1<S2。其中正确结论的个数是A、1 B、2 C、3 D、47. 如图,若抛物线y=x2-2x与x轴正半轴相交于点A,点P是y轴上一动点,过点P作直线l∥x轴,与抛物线相交于B,C两点(B在C的左侧),过点C作CD⊥x轴于点D,连接AB、DP,若OC将四边形BADP的面积分成2:1的两部分,则OC的解析式为( ) A、y=x B、y=2x C、y=4x D、y=8x8. 如图,在中, , , , 动点从点开始沿边向以的速度移动(不与点重合),动点从点开始沿边向以的速度移动(不与点重合).如果、分别从、同时出发,那么经过( )秒,四边形的面积最小.
A、y=x B、y=2x C、y=4x D、y=8x8. 如图,在中, , , , 动点从点开始沿边向以的速度移动(不与点重合),动点从点开始沿边向以的速度移动(不与点重合).如果、分别从、同时出发,那么经过( )秒,四边形的面积最小. A、0.5 B、1.5 C、3 D、49. 某店销售一款运动服,每件进价100元,若按每件128元出售,每天可卖出100件,根据市场调查结果,若每件降价1元,则每天可多卖出5件,要使每天获得的利润最大,则每件需要降价( )A、3元 B、4元 C、5元 D、8元10. 如图,四边形ABCD中,AB=AD , CE⊥BD , CE= BD . 若△ABD的周长为20cm,则△BCD的面积S(cm2)与AB的长x(cm)之间的函数关系式可以是( )
A、0.5 B、1.5 C、3 D、49. 某店销售一款运动服,每件进价100元,若按每件128元出售,每天可卖出100件,根据市场调查结果,若每件降价1元,则每天可多卖出5件,要使每天获得的利润最大,则每件需要降价( )A、3元 B、4元 C、5元 D、8元10. 如图,四边形ABCD中,AB=AD , CE⊥BD , CE= BD . 若△ABD的周长为20cm,则△BCD的面积S(cm2)与AB的长x(cm)之间的函数关系式可以是( )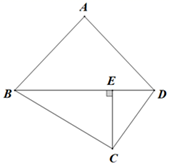 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
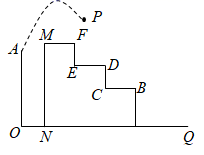
11. 如图所示,从高为2m的点 处向右上抛一个小球 ,小球路线呈抛物线 形状,小球水平经过2m时达到最大高度6m,然后落在下方台阶B处弹起,已知 m, m, m,若小球弹起形成一条与 形状相同的抛物线,且落点 与 , 在同一直线上,则小球弹起时的最大高度是m
 12. 如图,直线y=kx+b交坐标轴于A、B两点,交抛物线y=ax2于点C(4,3),且C是线段AB的中点,抛物线上另有位于第一象限内的一点P,过P的直线y=k′x+b′交坐标轴于D、E两点,且P恰好是线段DE的中点,若△AOB∽△DOE,则P点的坐标是.
12. 如图,直线y=kx+b交坐标轴于A、B两点,交抛物线y=ax2于点C(4,3),且C是线段AB的中点,抛物线上另有位于第一象限内的一点P,过P的直线y=k′x+b′交坐标轴于D、E两点,且P恰好是线段DE的中点,若△AOB∽△DOE,则P点的坐标是.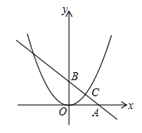 13. 如图,抛物线y=﹣ (x+1)(x﹣9)与坐标轴交于A、B、C三点,D为顶点,连结AC,BC.点P是该抛物线在第一象限内上的一点.过点P作y轴的平行线交BC于点E,连结AP交BC于点F,则 的最大值为.
13. 如图,抛物线y=﹣ (x+1)(x﹣9)与坐标轴交于A、B、C三点,D为顶点,连结AC,BC.点P是该抛物线在第一象限内上的一点.过点P作y轴的平行线交BC于点E,连结AP交BC于点F,则 的最大值为.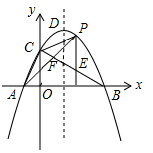 14. 已知抛物线 交x轴于点A,B (B在x轴正半轴上),交y轴于点C,△ABC是等腰三角形,则a的值为 .15. 如图,抛物线 (m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.
14. 已知抛物线 交x轴于点A,B (B在x轴正半轴上),交y轴于点C,△ABC是等腰三角形,则a的值为 .15. 如图,抛物线 (m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.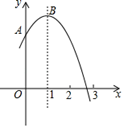
①抛物线 与直线y=m+2有且只有一个交点;
②若点 点 、点 在该函数图象上,则 ;
③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为 ;
④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为 ,其中正确判断的序号是
三、解答题
-
16. 如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,-3)
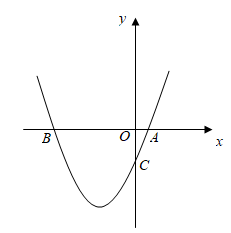
(1)、求此二次函数的解析式;(2)、在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.17. 为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为 ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=﹣0.01x2﹣20x+30000(0≤x≤1000).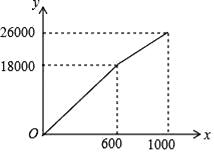 (1)、请直接写出k1、k2和b的值;(2)、设这块1000m2空地的绿化总费用为W(元),请利用W与x的函数关系式,求出绿化总费用W的最大值;(3)、若种草部分的面积不少于700m2 , 栽花部分的面积不少于100m2 , 请求出绿化总费用W的最小值.18. 如图,在平面直角坐标系中,△CDE的顶点C点坐标为C(1,﹣2),点D的横坐标为 , 将△CDE绕点C旋转到△CBO,点D的对应点B在x轴的另一个交点为点A.
(1)、请直接写出k1、k2和b的值;(2)、设这块1000m2空地的绿化总费用为W(元),请利用W与x的函数关系式,求出绿化总费用W的最大值;(3)、若种草部分的面积不少于700m2 , 栽花部分的面积不少于100m2 , 请求出绿化总费用W的最小值.18. 如图,在平面直角坐标系中,△CDE的顶点C点坐标为C(1,﹣2),点D的横坐标为 , 将△CDE绕点C旋转到△CBO,点D的对应点B在x轴的另一个交点为点A.(1)图中,∠OCE等于多少;
(2)求抛物线的解析式;
(3)抛物线上是否存在点P,使S△PAE=S△CDE?若存在,直接写出点P的坐标;若不存在,请说明理由.
 19. 如图,二次函数y=x2+bx﹣的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
19. 如图,二次函数y=x2+bx﹣的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.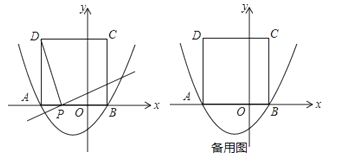
(1)b的值及点D的坐标。
(2)线段AO上是否存在点P(点P不与A、O重合),使得OE的长为1;
(3)在x轴负半轴上是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
四、综合题
-
20. 某某商店销售一种销售成本为 40 元/件的商品,销售一段时间后发现,每天的销量 y(件)与当天的销售单价 x (元/件)满足一次函数关系,并且当 x =20 时,y=1000,当 x =25 时,y=950.(1)、求出y与x的函数关系式,并写出自变量的取值范围;(2)、求出每件售价多少元时,商店销售该商品每天能获得最大利润,最大利润是多少元;(3)、如果该商店要使每天的销售利润不低于 13750 元,且每天的总成本不超过 20000 元,那么销售单价应控制在什么范围内?21. 定义:若函数(c≠0)与轴的交点A,B的横坐标为 , , 与轴交点的纵坐标为 , 若 , 中至少存在一个值,满足=(或=),则称该函数为友好函数.如图,函数与轴的一个交点A的横坐标为-3,与y轴交点C的纵坐标为-3,满足= , 称为友好函数.
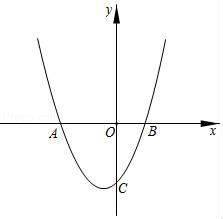 (1)、判断是否为友好函数,并说明理由;(2)、请探究友好函数表达式中的b与c之间的关系;(3)、若是友好函数,∠ACB为锐角,求c的取值范围.22. 如图,学校要在教学楼后面的空地上用40米长的竹篱笆围出一个矩形地块作生物园,矩形的一边用教学楼的外墙(外墙足够长),其余三边用竹篱笆围成.其中(即长不小于宽),设矩形的宽的长为x米,矩形面积为y平方米.
(1)、判断是否为友好函数,并说明理由;(2)、请探究友好函数表达式中的b与c之间的关系;(3)、若是友好函数,∠ACB为锐角,求c的取值范围.22. 如图,学校要在教学楼后面的空地上用40米长的竹篱笆围出一个矩形地块作生物园,矩形的一边用教学楼的外墙(外墙足够长),其余三边用竹篱笆围成.其中(即长不小于宽),设矩形的宽的长为x米,矩形面积为y平方米.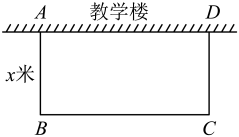 (1)、若矩形的面积150平方米,求宽的长;(2)、求y与x的函数关系式,并写出自变量x的取值范围;(3)、矩形地块的宽为多少时,矩形面积最大,并求出最大面积.23. 某公园对一块长 20m,宽10m的场地进行设计,方案如图所示.阴影区域为绿化区(四块全等的矩形),空白区域为活动区,且4个出口宽度相同,其宽度不小于4m,不大于8m.设出口长均为x(m),活动区面积为y(m).
(1)、若矩形的面积150平方米,求宽的长;(2)、求y与x的函数关系式,并写出自变量x的取值范围;(3)、矩形地块的宽为多少时,矩形面积最大,并求出最大面积.23. 某公园对一块长 20m,宽10m的场地进行设计,方案如图所示.阴影区域为绿化区(四块全等的矩形),空白区域为活动区,且4个出口宽度相同,其宽度不小于4m,不大于8m.设出口长均为x(m),活动区面积为y(m).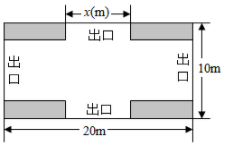 (1)、求y关于x的函数表达式:(2)、当x取多少时,活动区面积最大?最大面积是多少?(3)、若活动区布置成本为10元/m2 , 绿化区布置成本为8元/m2 , 布置场地的预算不超过1850元,当x为整数时,请求出符合预算且使活动区面积最大的x值及此时的布置成本.
(1)、求y关于x的函数表达式:(2)、当x取多少时,活动区面积最大?最大面积是多少?(3)、若活动区布置成本为10元/m2 , 绿化区布置成本为8元/m2 , 布置场地的预算不超过1850元,当x为整数时,请求出符合预算且使活动区面积最大的x值及此时的布置成本.