(人教版)2023-2024学年九年级数学上册22.3 实际问题与二次函数 同步分层训练(基础卷)
试卷更新日期:2023-07-16 类型:同步测试
一、选择题
-
1. 如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数解析式是 , 则该运动员此次掷铅球的成绩是( )
 A、6m B、12m C、8m D、10m2. 拱桥的形状是抛物线,其函数关系式为 , 当水面离桥顶的高度为m时,水面的宽度为( )米.
A、6m B、12m C、8m D、10m2. 拱桥的形状是抛物线,其函数关系式为 , 当水面离桥顶的高度为m时,水面的宽度为( )米. A、8 B、9 C、10 D、113. 如图,一个矩形的长比宽多3cm,矩形的面积是Scm2 . 设矩形的宽为xcm,当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数关系是( )
A、8 B、9 C、10 D、113. 如图,一个矩形的长比宽多3cm,矩形的面积是Scm2 . 设矩形的宽为xcm,当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数关系是( ) A、S=4x+6 B、S=4x-6 C、S=x2+3x D、S=x2-3x4. 小敏在某次投篮中,篮球的运动路线是抛物线 3.5的一部分(如图),若命中篮圈中心,则他与篮底的水平距离 是( )
A、S=4x+6 B、S=4x-6 C、S=x2+3x D、S=x2-3x4. 小敏在某次投篮中,篮球的运动路线是抛物线 3.5的一部分(如图),若命中篮圈中心,则他与篮底的水平距离 是( ) A、3.5m B、3.8m C、4m D、4.5m5. 如图,某农场拟建一间矩形奶牛饲养室,打算一边利用房屋现有的墙(墙足够长),其余三边除大门外用栅栏围成,栅栏总长度为50m,门宽为2m.若饲养室长为xm,占地面积为y ,则y关于x的函数表达式为( )
A、3.5m B、3.8m C、4m D、4.5m5. 如图,某农场拟建一间矩形奶牛饲养室,打算一边利用房屋现有的墙(墙足够长),其余三边除大门外用栅栏围成,栅栏总长度为50m,门宽为2m.若饲养室长为xm,占地面积为y ,则y关于x的函数表达式为( )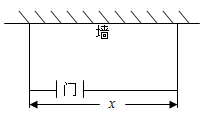 A、y=﹣ x2+26x(2≤x<52) B、y=﹣ x2+50x(2≤x<52) C、y=﹣x2+52x(2≤x<52) D、y=﹣ x2+27x﹣52(2≤x<52)6. 如图,一边靠学校院墙,其它三边用 米长的篱笆围成一个矩形花圃,设矩形 的边 米,面积为 平方米,则下面关系式正确的是( )
A、y=﹣ x2+26x(2≤x<52) B、y=﹣ x2+50x(2≤x<52) C、y=﹣x2+52x(2≤x<52) D、y=﹣ x2+27x﹣52(2≤x<52)6. 如图,一边靠学校院墙,其它三边用 米长的篱笆围成一个矩形花圃,设矩形 的边 米,面积为 平方米,则下面关系式正确的是( ) A、 B、 C、 D、7. 如图,用水管从某栋建筑物2.25m高的窗口A 处向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离OB是( )
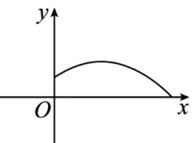
A、 B、 C、 D、7. 如图,用水管从某栋建筑物2.25m高的窗口A 处向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离OB是( )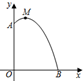 A、2.5米 B、3米 C、3.5米 D、4米8. 教练对小明推铅球的录像进行技术分析,发现某次铅球行进高度y(m)与水平距离x(m)之间的关系为y=- (x-4)2+3,由此可知小明这次的推铅球成绩是( )A、3m B、4m C、8m D、10m9. 2011年5月22日—29日在美丽的青岛市举行了苏迪曼杯羽毛球混合团体锦标赛.在比赛中,某次羽毛球的运动路线可以看作是抛物线y=- x2+bx+c的一部分(如图),其中出球点B离地面O点的距离是1m,球落地点A到O点的距离是4m,那么这条抛物线的解析式是( )
A、2.5米 B、3米 C、3.5米 D、4米8. 教练对小明推铅球的录像进行技术分析,发现某次铅球行进高度y(m)与水平距离x(m)之间的关系为y=- (x-4)2+3,由此可知小明这次的推铅球成绩是( )A、3m B、4m C、8m D、10m9. 2011年5月22日—29日在美丽的青岛市举行了苏迪曼杯羽毛球混合团体锦标赛.在比赛中,某次羽毛球的运动路线可以看作是抛物线y=- x2+bx+c的一部分(如图),其中出球点B离地面O点的距离是1m,球落地点A到O点的距离是4m,那么这条抛物线的解析式是( )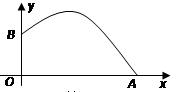 A、 B、 C、 D、10. 如图,一边靠学校院墙,其它三边用 40 米长的篱笆围成一个矩形花圃,设矩形 ABCD 的边 AB=x 米,面积为 S 平方米,则下面关系式正确的是( )
A、 B、 C、 D、10. 如图,一边靠学校院墙,其它三边用 40 米长的篱笆围成一个矩形花圃,设矩形 ABCD 的边 AB=x 米,面积为 S 平方米,则下面关系式正确的是( ) A、
A、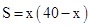 B、
B、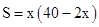 C、
C、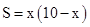 D、
D、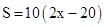
二、填空题
-
11. 一小球被抛出后,距离地面的高度h(米)和飞行时间t(秒)满足下面函数关系式 , 则小球距离地面的最大高度是米.12. 如图,若被击打的小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的关系为h=35t﹣5t2 , 则小球从飞出到落地所用时间为s.
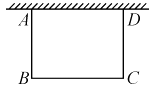
 13. 用长12m的铝合金条制成矩形窗框(如图所示),那么这个窗户的最大透光面积是(中间横框所占的面积忽略不计)
13. 用长12m的铝合金条制成矩形窗框(如图所示),那么这个窗户的最大透光面积是(中间横框所占的面积忽略不计) 14. 某种产品今年的年产量是20t,计划今后两年增加产量.如果每年的产量都比上一年增加x倍,两年后这种产品的产量y与x之间的函数表达式是 .15. 用一根长为 的铁丝,把它折成一个长方形框.设长方形的宽为 ,面积为 ,则 关于 的函数关系式是 .
14. 某种产品今年的年产量是20t,计划今后两年增加产量.如果每年的产量都比上一年增加x倍,两年后这种产品的产量y与x之间的函数表达式是 .15. 用一根长为 的铁丝,把它折成一个长方形框.设长方形的宽为 ,面积为 ,则 关于 的函数关系式是 .三、解答题
-
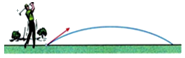
16. 某种爆竹点燃后,其上升高度h(米)和时间t(秒)符合关系式:h=v0t﹣ gt2(0<t<4),其中g以10米/秒2计算.这种爆竹点燃后以v0=20米/秒的初速度上升,问:这种爆竹在地面上点燃后,经过多少时间离地面最远?17. 如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=-5t2+20t,求小球飞行高度达到最高时的飞行时间.
 18. 如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m.设矩形的面积为 . 问长为多少时S最大,并求最大面积.
18. 如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m.设矩形的面积为 . 问长为多少时S最大,并求最大面积.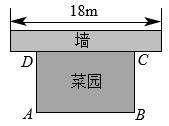 19. 利民商店销售一种进价为50元/件的土特产商品,当售价为60元/件,每周可卖出200件,若每件商品的售价每上涨1元,则每周就会少卖10件.求利民商店将售价上涨多少时每周可获得最大利润?最大利润是多少?
19. 利民商店销售一种进价为50元/件的土特产商品,当售价为60元/件,每周可卖出200件,若每件商品的售价每上涨1元,则每周就会少卖10件.求利民商店将售价上涨多少时每周可获得最大利润?最大利润是多少?四、综合题
-
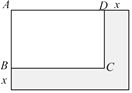
20. 商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施,经调查发现,每件商品每降价1元,商场每天可多售出2件,设每件商品降低x元据此规律,请回答:(1)、商场日销售量增加件,每件商品盈利元(用含x的代数式表示);(2)、在上述条件不变,销售正常的情况下,设商场日盈利y元,求y与x的函数关系式;(3)、在(2)的条件下,每件商品降价多少元时,商场日盈利最高?21. 某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的面积最大?下面是两位学生争议的情境:

请根据上面的信息,解决问题:
(1)、设AB=x米(x>0),试用含x的代数式表示BC的长;(2)、请你判断谁的说法正确,为什么?