（人教版）2023-2024学年九年级数学上册22.2 二次函数与一元二次方程同步分层训练（培优卷）

试卷更新日期：2023-07-16 类型：同步测试

进入出卷网下载

一、选择题

1. 二次函数 $y = a x^{2} + 2 a x + c$ （a，c为常数且 $a < 0$ ）经过 $(1 ， m)$ ，且 $m c < 0$ ，下列结论：① $c > 0$ ；② $a < - \frac{c}{3}$ ；③若关于x的方程 $a x^{2} + 2 a x = p - c (p > 0)$ 有整数解，则符合条件的p的值有3个；④当 $a \leq x \leq a + 2$ 时，二次函数的最大值为c，则 $a = - 4$ .其中一定正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 二次函数y＝ax²+bx+c（a≠0）的部分图象如图所示，其对称轴为直线x= $- \frac{1}{2}$ ，且与x轴的一个交点坐标为（﹣2，0）．下列结论：
①abc＞0；

②a＝b；

③图象与x轴的另一个交点坐标为（1，0）；

④关于x的一元二次方程ax²+bx+c﹣1＝0有两个相等的实数根；

⑤2a+c＝0．

其中正确的结论个数是（）

A、2 B、3 C、4 D、5

查看试题解析
3. 若二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与 $x$ 轴的交点坐标分别是 $(m ， 0)$ 、 $(n ， 0)$ ，且 $m < n$ ，图象上有一点 $M (p ， q)$ 在 $x$ 轴下方，对于以下说法：① $b^{2} - 4 a c > 0$ ；② $x = p$ 是方程 $a x^{2} + b x + c - q = 0$ 的解；③ $m < p < n$ ；④ $a (p - m) (p - n) < 0$ ，对于以上说法正确的是（）

A、①②③④ B、①②④ C、③④ D、①③

查看试题解析
4. 若二次函数y＝ax²＋bx－1的最小值为－3，则方程|ax²＋bx－1|＝2的不相同实数根的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
5. 已知抛物线y＝ax²＋bx＋c（a＜0）的对称轴为x＝－1，与x轴的一个交点为(2，0).若关于x的一元二次方程ax²＋bx＋c＝p（p＞0）有整数根，则p的值有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 如图，二次函数y=ax²+bx+c（a $\neq$ 0）的图象过点（-2，0），对称轴为直线x=1.有以下结论：
①abc>0；②8a+c>0；③若A（x₁ ， m），B（x₂ ， m）是抛物线上的两点，当x=x₁+x₂时，y=c；④若方程a（x+2）（4-x）=-2的两根为x₁ ， x₂ ，且x₁<x₂ ，则-2 $\leq$ x₁<x₂<4.其中结论正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 抛物线y=ax²+bx+c的顶点为D（﹣1，2），与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，其部分图象如图，则以下结论：①b²﹣4ac＜0；②a+b+c＜0；③c﹣a=2；④方程ax²+bx+c﹣2=0有两个相等的实数根．其中正确结论的个数为（）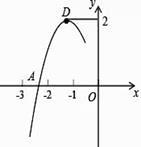

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，下列结论：
① $a b c < 0$ ；② $a + 2 b + 4 c \leq 0$ ；③方程 $a x^{2} + b x + c - 4 = 0$ 有两个相等的实数根；④方程 $a {(x - 1)}^{2} + b (x - 1) + c = 0$ 的两根是 $x_{1} = - 2$ ， $x_{2} = 2$

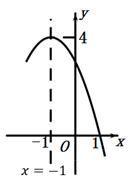
其中正确的结论有（）个.

A、1 B、2 C、3 D、4

查看试题解析
9. 二次函数y=ax²+bx+c（a≠0）的部分图象如图所示，图象过点（-1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c＞0；（4）若点A（-3，y₁）、点B（- $\frac{1}{2}$ ，y₂）、点C（ $\frac{7}{2}$ ，y₃）在该函数图象上，则y₁＜y₃＜y₂；（5）若方程a（x+1）（x-5）=-3的两根为x₁和x₂ ，且x₁＜x₂ ，则x₁＜-1＜5＜x₂ ．其中正确的结论有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
10. 下表是二次函数 $y = a x^{2} + b x + c$ 的 x，y的部分对应值：

则对于该函数的性质的判断：

①该二次函数有最大值； ②不等式y＞-1 的解集是x＜0 或x＞2；③ 方程 $a x^{2} + b x + c = 0$ 的两个实数根分别位于 $- \frac{1}{2} < x < 0$ 和 $2 < x < \frac{5}{2}$ 之间；④当x＞0 时，函数值y 随x 的增大而增大；

其中正确的是（）

A、②③ B、②④ C、①③ D、①④

查看试题解析

二、填空题

11. 如图，将二次函数 $y = x^{2} - m$ (其中 $m > 0$ )的图象在 $x$ 轴下方的部分沿 $x$ 轴翻折，图象的其余部分保持不变，形成新的图象记为 $y_{1}$ ，另有一次函数 $y = x + 2$ 的图象记为 $y_{2}$ ，若 $y_{1}$ 与 $y_{2}$ 恰有两个交点时，则 $m$ 的范围是.

查看试题解析
12. 已知二次函数y=a（x-x₁）（x-x₂）与x轴的交点是（1，0）和（3，0），关于x的方程a（x-x₁）（x-x₂）=m（m>0）的两个解分别为-1和5，关于x的方程a（x-x₁）（x-x₂）=n（其中m>n>0）也有两个整数解，则这两个整数解分别是．

查看试题解析
13. 当 $- 2 \leq x \leq 3$ 时，关于 $x$ 的一元二次方程 $x^{2} - 2 x + m - 2 = 0$ 只有一个实数解，则 $m$ 的取值范围为.

查看试题解析

14. 二次函数y=ax²+bx＋c的部分对应值列表如下：

x	…	-3	0	1	3	5	…
y	…	7	-8	-9	-5	7	…

则一元二次方程a(2x＋1)²+b(2x＋1)+c=-5的解为.

查看试题解析

15. 已知关于x的方程2+（x﹣m）（x﹣n）＝0，存在a，b是方程2+（x﹣m）（x﹣n）＝0的两个根，则实数m，n，a，b的大小关系可能是.

查看试题解析

三、解答题

16. 已知抛物线与x轴交于点 $A (- 2, 0)$ ， $B (4, 0)$ ，与y轴交于点 $C (0, 8)$ ，该抛物线的顶点为D．

(1)、求抛物线的解析式及其顶点D的坐标；

(2)、直线 $C D$ 的解析式为；

(3)、过点D作 $D H ⊥ x$ 轴于H ，在线段 $D H$ 上有一点P到直线 $C D$ 的距离等于线段 $P O$ 的长，求点P的坐标；

(4)、设直线 $C D$ 交x轴于点E ．过点B作x轴的垂线，交直线 $C D$ 于点F ，将抛物线沿其对称轴平移，使平移后的抛物线与线段 $E F$ 总有公共点．试探究：抛物线向上最多可平移多少个单位长度？向下最多可平移多少个单位长度？

查看试题解析
17. 已知：二次函数 $y = x^{2} - m x + m - 2$ ，求证：无论m为任何实数，该二次函数的图象与x轴都在两个交点；

查看试题解析
18. 在二次函数的学习中，教材有如下内容：

小聪和小明通过例题的学习，体会到利用函数图象可以求出方程的近似解.于是他们尝试利用图象法探究方程 $x^{3} - 2 x^{2} + 1 = 0$ 的近似解，做法如下：

请你选择小聪或小明的做法，求出方程 $x^{3} - 2 x^{2} + 1 = 0$ 的近似解(精确到0.1).

查看试题解析
19. 已知二次函数y=kx²﹣2x﹣1的图像与x轴有两个不同的交点，求实数k的取值范围．

查看试题解析

四、综合题

20. 已知函数 $y = x^{2} + b x + c$ （ $b$ ， $c$ 为常数）的图象经过点 $(0 ， 3)$ ， $(6 ， 3)$ .

(1)、求 $b$ ， $c$ 的值；

(2)、当 $0 \leq x \leq 4$ 时，求 $y$ 的最大值与最小值之差；

(3)、当 $k - 4 \leq x \leq k$ 时，若 $y$ 的最大值与最小值之差为8，求 $k$ 的值.

查看试题解析
21. 阅读与思考：下面是小明同学的数学小论文，请仔细阅读并完成相应的任务．
用函数观点认识一元二次方程根的情况

我们知道，一元二次方程ax²+bx+c=0(a≠0)的根就是相应的二次函数y=ax²+bx+c(a≠0)的图像(抛物线)与x轴交点的横坐标．抛物线与x轴的交点有三种情况：有两个交点、有一个交点、无交点与此相对应，一元二次方程的根也有三种情况：有两个不相等的实数根、有两个相等的实数根、无实数根．因此可用抛物线与x轴的交点个数确定一元二次方程根的情况．

下面根据抛物线的顶点坐标( $- \frac{b}{2 a}$ ， $\frac{4 a c - b^{2}}{4 a}$ ）和一元二次方程根的判别式△=b²-4ac，分a>0和a<0两种情况进行分析：
当a>0时，抛物线开口向上．

①当△=b²-4ac>0时，有4ac-b²<0．

∵a>0，∴顶点纵坐标 $\frac{4 a c - b^{2}}{4 a}$ <0，

∴顶点在x轴的下方，抛物线与x轴有两个交点(如图①)，

∴一元二次方程ax²+bx+c=0(a≠0)有两个不相等的实数根．

②当△=b²-4ac=0时，有4ac-b²=0．

∵a>0，∴顶点纵坐标 $\frac{4 a c - b^{2}}{4 a}$ =0，

∴顶点在x轴上，抛物线与x轴有一个交点(如图②)，

∴一元二次方程ax²+bx+c=0(a≠0)有两个相等的实数根，

③当△=b²-4ac<0……
当a<0时，抛物线开口向下．

……

任务：

(1)、上面小论文中的分析过程，主要运用的数学思想是(从下面选项中选出两个即可)
A．数形结合

B．统计思想

C．分类讨论

D．转化思想

(2)、请参照小论文中当a>0时①②的分析过程，写出③中当a>0，△<0时，一元二次方程根的情况的分析过程，并画出相应的示意图．

(3)、实际上，除一元二次方程外，初中数学还有一些知识也可以用函数观点来认识，例如：可用函数观点来认识一元一次方程的解，请你再举出一例．

查看试题解析
22. 已知：抛物线 $y = a x^{2} + x + 4 (a \neq 0)$ 与x轴交于A、B两点，点A在点B的左侧，与y轴交于点C．直线 $y = 6$ ，与抛物线交于E、F两点．

(1)、若 $E F = 9$ ，求a的值；

(2)、若抛物线的对称轴为 $x = 1$ ．
①求 $△ A B C$ 的面积；

②当 $0 \leq x \leq 6$ 时，求函数最大值与最小值的差；

(3)、当 $x \geq \frac{1}{2}$ 时，若抛物线的最高点到直线 $y = 6$ 的距离为1，直接写出a的值．

查看试题解析
23. 阅读下列材料
我们通过下列步骤估计方程2x²+x﹣2=0的根的所在的范围．

第一步：画出函数y=2x²+x﹣2的图象，发现图象是一条连续不断的曲线，且与x轴的一个交点的横坐标在0，1之间．

第二步：因为当x=0时，y=﹣2＜0；当x=1时，y=1＞0．

所以可确定方程2x²+x﹣2=0的一个根x₁所在的范围是0＜x₁＜1．

第三步：通过取0和1的平均数缩小x₁所在的范围；

取x= $\frac{0 + 1}{2} = \frac{1}{2}$ ，因为当x= $\frac{1}{2}$ 时，y＜0，

又因为当x=1时，y＞0，

所以 $\frac{1}{2}$ ＜x₁＜1．

(1)、请仿照第二步，通过运算，验证2x²+x﹣2=0的另一个根x₂所在范围是﹣2＜x₂＜﹣1；

(2)、在﹣2＜x₂＜﹣1的基础上，重复应用第三步中取平均数的方法，将x₂所在范围缩小至m＜x₂＜n，使得n﹣m≤ $\frac{1}{4}$ ．

查看试题解析

（人教版）2023-2024学年九年级数学上册22.2 二次函数与一元二次方程 同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年九年级数学上册22.2 二次函数与一元二次方程同步分层训练（培优卷）