(人教版)2023-2024学年九年级数学上册22.2 二次函数与一元二次方程 同步分层训练(基础卷)
试卷更新日期:2023-07-16 类型:同步测试
一、选择题
-
1. 如表是一组二次函数y=x2﹣x﹣3的自变量和函数值的关系,那么方程x2﹣x﹣3=0的一个近似根是( )
x
1
2
3
4
y
﹣3
﹣1
3
9
A、1.2 B、2.3 C、3.4 D、4.52. 根据以下表格中二次函数y=ax2+bx+c的自变量x与函数值y的对应值,可以判断方程ax2+bx+c=0的一个解x的范围是( )x
0
0.5
1
1.5
2
y=ax2+bx+c
﹣1
﹣0.5
1
3.5
7
A、0<x<0.5 B、0.5<x<1 C、1<x<1.5 D、1.5<x<23. 已知关于x的一元二次方程ax2+bx+c=0有两个相等的实数根,则抛物线y=ax2+bx+c与x轴的交点个数是( )A、0个 B、1个 C、2个 D、3个4. 如图,二次函数y=ax2+bx+c(a<0)的图象经过原点O,与x轴另一个交点为A点,则方程ax2+bx+c=0的解是( )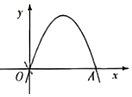 A、两个正根 B、两个负根 C、一个正根,一个负根 D、0和一个正根5. 若方程ax2+bx+c=0(a>0)的两个根是﹣3和1,则对于二次函数y=ax2+bx+c,当y>0时,x的取值范围是( )A、﹣3<x<1 B、x<﹣3或x>1 C、x>﹣3 D、x<16. 下表是满足二次函数 的五组数据, 是方程 的一个解,则下列选项中正确的是( )
A、两个正根 B、两个负根 C、一个正根,一个负根 D、0和一个正根5. 若方程ax2+bx+c=0(a>0)的两个根是﹣3和1,则对于二次函数y=ax2+bx+c,当y>0时,x的取值范围是( )A、﹣3<x<1 B、x<﹣3或x>1 C、x>﹣3 D、x<16. 下表是满足二次函数 的五组数据, 是方程 的一个解,则下列选项中正确的是( )1.6
1.8
2.0
2.2
2.4
-0.80
-0.54
-0.20
0.22
0.72
A、 B、 C、 D、7. 如图,小明在某次投篮中,球的运动路线是抛物线y=﹣0.2x2+3.5的一部分,若命中篮圈中心,则他与篮圈底的距离l是( ) A、3m B、3.5m C、4m D、4.5m8. 函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )A、k<3 B、k<3且k≠0 C、k≤3 D、k≤3且k≠09. 如图,二次函数y=ax2+bx+c的图象与x轴相交于(-2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是( )
A、3m B、3.5m C、4m D、4.5m8. 函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )A、k<3 B、k<3且k≠0 C、k≤3 D、k≤3且k≠09. 如图,二次函数y=ax2+bx+c的图象与x轴相交于(-2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是( )
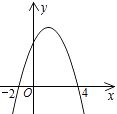
A、x<-2 B、-2<x<4 C、x>0 D、x>410. 根据以下表格中二次函数y=ax2+bx+c的自变量x与函数值y的对应值,可以判断方程ax2+bx+c=0的一个解x的范围是( )x
0
0.5
1
1.5
2
y=ax2+bx+c
-1
-0.5
1
3.5
7
A、0<x<0.5 B、0.5<x<1 C、1<x<1.5 D、1.5<x<2二、填空题
-
11. 已知抛物线的部分图象如图所示,则方程的解是
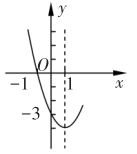 12. 如图,在平面直角坐标系 中,抛物线 的对称轴为直线 ,与x轴的一个交点为 ,则关于x的方程 的解为 .
12. 如图,在平面直角坐标系 中,抛物线 的对称轴为直线 ,与x轴的一个交点为 ,则关于x的方程 的解为 .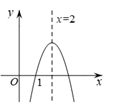 13. 已知二次函数 的部分图象如图所示,则关于x的一元二次方程 的解为.
13. 已知二次函数 的部分图象如图所示,则关于x的一元二次方程 的解为. 14. 已知抛物线y=ax2+bx+c 与x 轴交于A(-1,0),B(5,0),则一元二次方程ax2+bx+c=0的根是 .15. 已知抛物线 的图像与x轴分别交于点 , ,则关于x的方程 的根为 .
14. 已知抛物线y=ax2+bx+c 与x 轴交于A(-1,0),B(5,0),则一元二次方程ax2+bx+c=0的根是 .15. 已知抛物线 的图像与x轴分别交于点 , ,则关于x的方程 的根为 .三、解答题
-
16. 已知二次函数y=ax2+bx+c的图象过点 , 且对任意实数x,都有.二次函数与x轴的正半轴交点为A,与y轴交点为C;点M是中二次函数图象上的动点.在x轴上存在点N,使得以A、C、M、N为顶点的四边形是平行四边形.请求出所有满足条件的点N的坐标.17. 若二次函数的对称轴为直线 , 求关于x的方程的解.18. 已知抛物线 经过 、 两点,求关于x的一元二次方程 的解.19. 已知二次函数 试证明:不论m取何值,这个二次函数的图象必与x轴有两个交点
四、综合题
-
20. 已知函数( , 为常数)的图象经过点 , .(1)、求 , 的值;(2)、当时,求的最大值与最小值之差;(3)、当时,若的最大值与最小值之差为8,求的值.21. 某水果批发商场经销一种水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价格不变的情况下,若每千克每涨价1元,日销售量将减少20千克.(1)、设每千克涨价为元,每天的总盈利为元.若涨价为整数,则总盈利最大值为多少?(2)、若商场只要求保证每天的盈利为6000元,每千克应涨价多少元?22. 已知二次函数.(1)、证明:二次函数的图象与x轴总有交点.(2)、若点和点在该二次函数图象上,求的值.(3)、将该二次函数图象向下平移2个单位,令新函数图象与x轴的交点横坐标为x1 , x2.
证明:.
23. 某运动器材批发市场销售一种篮球,每个篮球进价为50元,规定每个篮球的售价不低于进价,经市场调查,每月的销售量y(个)与每个篮球的售价x(元)满足一次函数关系,部分数据如下表:售价x
60
62
64
销售量y
500
480
460
(1)、求y与x之间的函数关系式;(不需求自变量x的取值范围)(2)、该批发市场每月想从这种篮球销售中获利8000元,又想尽量多给客户实惠,应如何给这种篮球定价?(3)、物价部门规定,该篮球的每个利润不允许高于进货价的50%,设销售这种篮球每月的总利润为w(元),那么销售单价定为多少元可获得最大利润?最大利润是多少?