2023年浙教版数学七年级上册第一章有理数单元测试（B卷）

试卷更新日期：2023-07-16 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 在 $- 2022$ ， $- \frac{1}{7}$ ， $- (- 3)$ ， 0， ${(- 4)}^{2}$ ， $| - 2 |$ 中，既是负数又是整数的有（）

A、1个 B、2 C、3个 D、4个

查看试题解析
2. 在生产图纸上通常用 $\emptyset 30 0_{- 0.5}^{+ 0.2}$ 来表示轴的加工要求，这里 $\emptyset 300$ 表示直径是 $300 m m$ ， $+ 0.2$ 和 $- 0.5$ 是指直径在 $(300 - 0.5) m m$ 到 $(300 + 0.2) m m$ 之间的产品都属于合格产品.现加工一批轴，尺寸要求是 $\emptyset 4 5_{- 0.3}^{+ 0.2}$ ，则下面产品合格的是（）

A、 $44.6 m m$ B、 $44.8 m m$ C、 $45.3 m m$ D、 $45.5 m m$

查看试题解析
3. 如图，数轴的单位长度为1，若点 $A$ ， $B$ 表示的数互为相反数，那么点 $C$ 表示的数是（）

A、2 B、1 C、-2 D、-1

查看试题解析
4. 数轴上的点B到原点的距离是6，则点B表示的是为（）

A、12或 $- 12$ B、6 C、 $- 6$ D、6或 $- 6$

查看试题解析
5. 小明在写作业时不慎将两滴墨水滴在数轴上，如图所示，此时墨迹盖住的整数共有（）个.

A、3 B、4 C、5 D、6

查看试题解析
6. 已知 $a$ ， $b$ 都是有理数，如果 $| a + b | = b - a$ ，那么对于下列两种说法： $① a$ 可能是负数； $② b$ 一定不是负数，其中判断正确的是（）

A、 $① ②$ 都错 B、 $① ②$ 都对 C、 $①$ 错 $②$ 对 D、 $①$ 对 $②$ 错

查看试题解析
7. 若|m－1|＝－m＋1，则m一定（）

A、大于1 B、小于1 C、不大于1 D、不小于1

查看试题解析
8. 某茶叶厂抽检四盒茶叶的质量(单位：g)，把超过标准质量的克数记为正数，不足标准质量的克数记为负数，结果是：+1.3，-2.2，+0.9，-0.7，其中最接近标准质量的是（）

A、+1.3 B、-2.2 C、+0.9 D、-0.7

查看试题解析
9. 有理数 $m$ ， $n$ 在数轴上的对应点的位置如图所示，则正确的结论是（）

A、 $n > 3$ B、 $m < - 1$ C、 $m > - n$ D、 $| m | > | n |$

查看试题解析
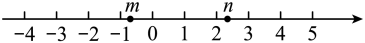10. 下列说法中正确的个数是（）
①0是绝对值最小的有理数 ②相反数大于本身的数是负数 ③一个有理数不是整数就是分数 ④一个有理数不是正数就是负数

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（每空4分，共24分）

11. $d$ 是最大的负整数， $e$ 是最小的正整数， $f$ 的相反数等于它本身，则 $d - e + 2 f$ 的值是．

查看试题解析
12. 红富士苹果的包装箱上标明苹果质量为 $15 k g_{- 0.03 k g}^{+ 0.02 k g}$ ，如果某箱苹果重14.95 kg，那么这箱苹果标准.(填“符合”或“不符合”)

查看试题解析
13. 数轴上，一只蚂蚁从点 $A$ 爬行4个单位长度到了表示 $- 3$ 的点 $B$ ，则点 $A$ 表示的数是．

查看试题解析
14. $| a | = 4$ ， $| b | = a - 2$ ，则 $a - b$ 的值是．

查看试题解析
15. 式子4+|x﹣1|能取得的最小值是，这时x＝；式子3﹣|2x﹣1|能取得的最大值是，这时x＝．

查看试题解析
16. a、b是有理数，它们在数轴上的对应点的位置如下图所示，把a、 $-$ a、0、b、 $-$ b按照从小到大并用“＜”连接为．

查看试题解析

三、解答题（共8题，共66分）

17. 把下列各数分别填入相应的集合里.
$- 5$ ， $| - \frac{3}{4} |$ ， 0， $- 3.14$ ， $\frac{22}{7}$ ， 2006，+1.99， $- (- 6)$ ， 0.010010001…，15%

（ 1 ）负数集合：{          …}；

（ 2 ）分数集合：{          …}；

（ 3 ）非负整数集合：{          …}；

（ 4 ）有理数集合：{          …}.

查看试题解析
18. 已知有理数a，b，如图数a在数轴上对应的点是点A，b是负数，且b在数轴上对应的点与原点的距离为3.5.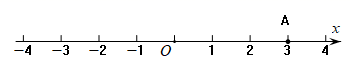

(1)、a＝， b＝

(2)、将 $- 2 \frac{1}{2}$ ，0，－(－2)，b在如图的数轴上表示出来，并用“<”连接这些数.

查看试题解析
19. 某食品厂从生产的食品中抽出样品20袋，检测每袋的质量是否符合标准，超过的部分用正数表示，不足的部分用负数表示，记录如表：
与标准质量的差值（克）
﹣5
﹣2
0
1
3
6
袋数（袋）
2
4
5
5
1
3

(1)、若每袋标准质量为350克，则这批抽样检测的样品的总质量是多少克？

(2)、若该食品的包装袋上标有产品合格要求为“净重350±2克”，则这批样品的合格率为多少？

查看试题解析
20. 如图，快递员小刘要从公司点 $A$ 处出发，前往 $B$ ， $C$ ， $D$ 等地派送包裹，规定：向上向右走为正，向下向左走为负，并且行走方向顺序为先左右再上下.若从 $A$ 到 $B$ 记为： $A \to B (+ 1 ， + 4)$ ，从 $B$ 到 $A$ 记为： $B \to A (- 1 ， - 4)$ ，其中第一个数表示左右方向，第二个数表示上下方向.

(1)、A→C（，），B→D（，），C→D（，），

(2)、若快递员小刘的行走路线为 $A \to B \to C \to D$ ，请计算该快递员走过的路程；

(3)、若快递员小刘从 $A$ 处去某 $E$ 处的行走路线依次为 $(+ 2 ， + 2)$ ， $(+ 1 ， - 1)$ ， $(- 2 ， + 3)$ ， $(- 1 ， - 2)$ ，请在图中标出 $E$ 的位置.

查看试题解析
21. 同学们都知道，|4-(-2)|表示4与-2的差的绝对值，实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离；同理|x-3|也可理解为x与3两数在数轴上所对应的两点之间的距离.试探索：

(1)、|4-(-2)|=

(2)、若|x-2|=5，求x的值；

(3)、求|x-1|+|x+2|的最小值

查看试题解析
22. 如图，在数轴上点A表示数a，点B表示数b，点C表示数c，点A到点B的距离记为 $A B$ ，我们规定： $A B$ 的大小可以用位于右边的点表示的数减去左边的点表示的数表示，即 $A B = b - a$ .其中b是最大的负整数，a，c满足 $| a + 3 |$ 与 ${(c - 5)}^{2}$ 互为相反数.

(1)、 a= ， b= ， c=；

(2)、以某点D为折点，将此数轴向右对折，若点A在点C的右边，且 $A C = 2$ ，则D表示的数是；

(3)、若点A以每秒2个单位长度的速度向右运动t秒时， $5 A B = A C$ .求出t的值.

查看试题解析
23. 已知点A，B在数轴上分别表示有理数a，b，点A，B之间的距离表示为AB.当A，B两点中有一点在原点时，不妨设点A在原点，如图1，AB＝OB＝|b|－|a|＝b－a＝|a－b|.当A，B两点都不在原点时，
①如图2，点A，B都在原点的右边，AB＝OB－OA＝|b|－|a|＝b－a＝|a－b|；
②如图3，点A，B都在原点的左边，AB＝OB－OA＝|b|－|a|＝－b－（－a）＝a－b＝|a－b|；
③如图4，点A，B在原点的两边，AB＝OA＋OB＝|a|＋|b|＝a＋（－b）＝a－b＝|a－b|.
综上数轴上A，B两点之间的距离AB＝|a－b|，如数轴上表示4和－1的两点之间的距离是|4－（－1）|＝5
利用上述结论，解答以下问题：

(1)、若数轴上表示有理数a和－2的两点之间的距离是3，则a＝；

(2)、若数轴上表示数a的点位于-5与2之间，求|a+5|+|a-2|的值；

(3)、若整数x，y满足（|x－1|＋|x＋3|）（|y＋1|＋|y－2|）＝12，求代数式x＋y的最小值和最大值.

查看试题解析
24. 对于含绝对值的算式，在有些情况下，可以不需要计算出结果也能将绝对值符号去掉，例如：｜7-6｜=7-6；｜6-7｜=7-6； $| \frac{1}{2} - \frac{1}{3} | = \frac{1}{2} - \frac{1}{3}$ ； $| \frac{1}{3} - \frac{1}{2} | = \frac{1}{2} - \frac{1}{3}$ ．
观察上述式子的特征，解答下列问题：

(1)、把下列各式写成去掉绝对值符号的形式（不用写出计算结果）：
①｜23-47｜=；② $| \frac{2}{3} - \frac{2}{5} |$ =；

(2)、当a>b时，｜a-b｜=；当a<b时，｜a-b｜=；

(3)、计算： $| \frac{1}{2} - 1 | + | \frac{1}{3} - \frac{1}{2} | + | \frac{1}{4} - \frac{1}{3} | + \dots + | \frac{1}{2022} - \frac{1}{2021} |$ ．

查看试题解析

与标准质量的差值（克）	﹣5	﹣2	0	1	3	6
袋数（袋）	2	4	5	5	1	3

2023年浙教版数学七年级上册第一章 有理数 单元测试（B卷）

一、选择题（每题3分，共30分）

二、填空题（每空4分，共24分）

三、解答题（共8题，共66分）

2023年浙教版数学七年级上册第一章有理数单元测试（B卷）