2023年浙教版数学七年级上册1.3绝对值 同步测试(培优版)
试卷更新日期:2023-07-16 类型:同步测试
一、选择题(每题4分,共40分)
-
1. 如图,数轴的单位长度为1.若点B和点C所表示的两个数的绝对值相等,则点A,D表示的数分别是( )
 A、 , 1 B、 , 3 C、 , 2 D、 , 42. 若a、b都是有理数且都不为零,则式子 值为( )A、0或-2 B、2或-2 C、0或2 D、0或±23. 已知a,b,c为非零有理数,则的值不可能为( )A、0 B、-3 C、-1 D、34. 如图,图中数轴的单位长度为1.如果点B , C表示的数的绝对值相等,那么点A表示的数是()
A、 , 1 B、 , 3 C、 , 2 D、 , 42. 若a、b都是有理数且都不为零,则式子 值为( )A、0或-2 B、2或-2 C、0或2 D、0或±23. 已知a,b,c为非零有理数,则的值不可能为( )A、0 B、-3 C、-1 D、34. 如图,图中数轴的单位长度为1.如果点B , C表示的数的绝对值相等,那么点A表示的数是() A、 B、 C、 D、5. 有理数在数轴上的位置如图所示,则的值为( )
A、 B、 C、 D、5. 有理数在数轴上的位置如图所示,则的值为( ) A、 B、 C、 D、6. 若 , 则的取值可能是( ).A、±3 B、±1或±3 C、±1 D、-1或37. 若a表示一个有理数,且有|﹣3﹣a|=3+|a|,则a应该是( )A、任意一个有理数 B、任意一个正数 C、任意一个负数 D、任意一个非负数8. 已知a,b是有理数, , ,若将a,b在数轴上表示,则图中有可能( )A、
A、 B、 C、 D、6. 若 , 则的取值可能是( ).A、±3 B、±1或±3 C、±1 D、-1或37. 若a表示一个有理数,且有|﹣3﹣a|=3+|a|,则a应该是( )A、任意一个有理数 B、任意一个正数 C、任意一个负数 D、任意一个非负数8. 已知a,b是有理数, , ,若将a,b在数轴上表示,则图中有可能( )A、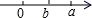 B、
B、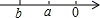 C、
C、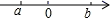 D、
D、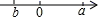 9. 若a≠0,b≠0,则代数式 的取值共有( )A、2个 B、3个 C、4个 D、5个10. 已知0≤a≤4,那么|a﹣2|+|3﹣a|的最大值等于( )A、1 B、5 C、8 D、3
9. 若a≠0,b≠0,则代数式 的取值共有( )A、2个 B、3个 C、4个 D、5个10. 已知0≤a≤4,那么|a﹣2|+|3﹣a|的最大值等于( )A、1 B、5 C、8 D、3二、填空题(每空5分,共30分)
-
11. 实数a,b满足 , 则的最小值为.12. m是常数,若式子的最小值是6,则m的值是.13. 若 , , 则n的值为 .14. 式子|x﹣1|+|x﹣2|+|x﹣3|+|x﹣4|+|x﹣5|+|x﹣6|+|x﹣7|+|x﹣8|+|x﹣9|+|x﹣10|的最小值是 .15. 已知m、n是两个非零有理数,则=16. 已知有理数a、b满足 , 则 .
三、解答题(共4题,共30分)
-
17. 同学们都知道,表示7与-1之差的绝对值,实际上也可理解为7与-1两数在数轴上所对的两点之间的距离.如的几何意义是数轴上表示有理数的点与表示有理数6的点之间的距离.试探索∶(1)、求;若 , 则;(2)、的最小值是;(3)、当时,的最小值是;(4)、已知则求出的最大值和最小值.18. 结合数轴与绝对值的知识回答下列问题:
 (1)、数轴上表示6和2的两点之间的距离为|6-2|=;
(1)、数轴上表示6和2的两点之间的距离为|6-2|=;表示-1和2两点之间的距离为|(-1)-(+2)|=|-1-2|=;
一般地,数轴上表示数m和数n的两点之间的距离等于|m-n|,
如果表示数a和-1的两点之间的距离是3,那么a= .
(2)、若数轴上表示数a的点位于-5与3之间(包括-5与3两点),求|a+5|+|a-3|的值;(3)、当x=时,|x+1|+|x+5|+|x-3|的值最小,最小值为 .(4)、当x,y满足|x+1|+|x-2|+|y+3|+|y-4|=10时,x-3y的最大值为 .19. 学们,我们都知道:|5-2|表示5与2的差的绝对值,实际上也可理解为5与2两数在数轴上所对应的两点之间的距离;|5+2|表示5与-2的差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离,试探索:(1)、|-4+6|=;|-2-4|=;(2)、找出所有符合条件的整数x,使|x+2|+|x-1|=3成立;(3)、若数轴上表示数a的点位于-4与6之间,求|a+4|+|a-6|的值;
(4)、当a=时,|a-1|+|a+5|+|a-4|的值最小,最小值是;20. 阅读下列材料并解决有关问题:我们知道 , 所以当时,;当时, , 现在我们可以用这个结论来解决下面问题:(1)、已知 , 是有理数,当时,求的值;(2)、已知 , , 是有理数,当 , 求的值;(3)、已知 , , 是有理数, , , 求的值.