2023年高考数学真题分类汇编2：导数及其应用、不等式

试卷更新日期：2023-07-16 类型：二轮复习

进入出卷网下载

一、填空题

1. 设x，y满足约束条件 ${\begin{array}{l} - 2 x + 3 y \leq 3 \\ 3 x - 2 y \leq 3 \\ x + y \geq 1 \end{array}$ ，设 $z = 3 x + 2 y$ ，则z的最大值为．

查看试题解析
2. 在 $△ A B C$ 中， $∠ A = 6 0^{∘}$ ， $B C = 1$ ，点 $D$ 为 $A B$ 的中点，点 $E$ 为 $C D$ 的中点，若设 $\vec{A B} = \vec{a} ， \vec{A C} = \vec{b}$ ，则 $\vec{A E}$ 可用 $\vec{a} ， \vec{b}$ 表示为；若 $\vec{B F} = \frac{1}{3} \vec{B C}$ ，则 $\vec{A E} \cdot \vec{A F}$ 的最大值为．

查看试题解析
3. 设 $a \in (0 ， 1)$ ，若函数 $f (x) = a^{x} + {(1 + a)}^{x}$ 在 $(0 ， + ∞)$ 上单调递增，则a的取值范围是.

查看试题解析
4. 若x，y满足约束条件 ${\begin{array}{l} x - 3 y \leq - 1 \\ x + 2 y \leq 9 \\ 3 x + y \geq 7 \end{array}$ ，则 $z = 2 x - y$ 的最大值为.

查看试题解析
5. 公园修建斜坡，假设斜坡起点在水平面上，斜坡与水平面的夹角为 $θ$ ，斜坡终点距离水平面的垂直高度为4米，游客每走一米消耗的体能为 $(1.025 - c o s θ)$ ，要使游客从斜坡底走到斜坡顶端所消耗的总体能最少，则 $θ =$ ；

查看试题解析

二、选择题

6. 曲线 $y = \frac{e^{x}}{x + 1}$ 在点 $(1 ， \frac{e}{2})$ 处的切线方程为（）

A、 $y = \frac{e}{4} x$ B、 $y = \frac{e}{2} x$ C、 $y = \frac{e}{4} x + \frac{e}{4}$ D、 $y = \frac{e}{2} x + \frac{3 e}{4}$

查看试题解析
7. 函数 $f (x)$ 的图象如下图所示，则 $f (x)$ 的解析式可能为（）

A、 $\frac{5 (e^{x} - e^{- x})}{x^{2} + 2}$ B、 $\frac{5 s i n x}{x^{2} + 1}$ C、 $\frac{5 (e^{x} + e^{- x})}{x^{2} + 2}$ D、 $\frac{5 c o s x}{x^{2} + 1}$

查看试题解析
8. 已知实数 $x ， y$ 满足 $x^{2} + y^{2} - 4 x - 2 y - 4 = 0$ ，则 $x - y$ 的最大值是（）

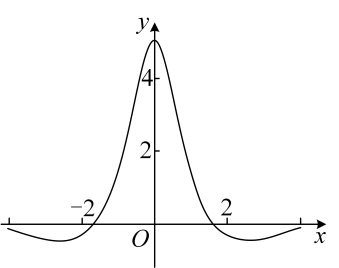A、 $1 + \frac{3 \sqrt{2}}{2}$ B、4 C、 $1 + 3 \sqrt{2}$ D、7

查看试题解析
9. 已知函数f(x)= $a e^{x} - l n x$ 在区间 $(1 ， 2)$ 单调递增，则a的最小值为（）

A、 $e^{2}$ B、 $e$ C、 $e^{- 1}$ D、 $e^{- 2}$

查看试题解析
10. 若f(x)=alnx+ $\frac{b}{x}$ + $\frac{c}{x^{2}}$ (a≠0)既有极大值也有极小值，则（）

A、bc>0 B、ab>0 C、 $b^{2} + 8 a c > 0$ D、ac<0

查看试题解析
11. 已知集合M={−2，−1，0，1，2}，N={x|x²−x−6⩾0}，则M∩N=（）

A、{−2，−1，0，1} B、{0，1，2} C、{−2} D、{2}

查看试题解析

12. 噪声污染问题越来越受到重视，用声压级来度量声音的强弱，定义声压级

L_{p} =

20 \times l g \frac{p}{p_{0}}

，其中常数

p_{0} (p_{0} > 0)

是听觉下限间值，

p

是实际声压. 下表为不同声源的声压级：

声源	与声源的距离/m	声压级/dB
燃油汽车	10	60~90
混合动力汽车	10	50～60
电动汽车	10	40

已知在距离燃油汽车、混合动力汽车、电动汽车 $10 m$ 处测得实际声压分别为 $p_{1} ， p_{2} ， p_{3}$ ，则（）

A、

p_{1} ⩾ p_{2}

B、

p_{2} > 10 p_{3}

C、

p_{3} = 100 p_{0}

D、

p_{1} ⩽ 100 p_{2}

查看试题解析

三、解答题

13. 已知 $f (x) = a x - \frac{s i n x}{c o s^{3} x} ， x \in (0 ， \frac{π}{2})$

(1)、若 $a = 8$ ，讨论 $f (x)$ 的单调性；

(2)、若 $f (x) < s i n 2 x$ 恒成立，求a的取值范围．

查看试题解析
14. 已知函数 $f (x) = a x - \frac{s i n x}{c o s^{2} x} ， x \in (0 ， \frac{π}{2})$ ．

(1)、当 $a = 1$ 时，讨论 $f (x)$ 的单调性；

(2)、若 $f (x) + s i n x < 0$ ，求 $a$ 的取值范围．

查看试题解析
15. 已知函数 $f (x) = (\frac{1}{x} + \frac{1}{2}) l n (x + 1)$ ．

(1)、求曲线 $y = f (x)$ 在 $x = 2$ 处切线的斜率；

(2)、当 $x > 0$ 时，证明： $f (x) > 1$ ；

(3)、证明： $\frac{5}{6} < l n (n!) - (n + \frac{1}{2}) l n (n) + n \leq 1$ ．

查看试题解析
16. 已知函数 $f (x) = (\frac{1}{x} + a) l n (1 + x)$ .

(1)、当 $a = - 1$ 时，求曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的切线方程；

(2)、是否存在a，b，使得曲线 $y = f (\frac{1}{x})$ 关于直线 $x = b$ 对称，若存在，求a，b的值，若不存在，说明理由.

(3)、若 $f (x)$ 在 $(0 ， + ∞)$ 存在极值，求a的取值范围.

查看试题解析
17. 已知函数 $f (x) = (\frac{1}{x} + a) l n (1 + x)$ .

(1)、当 $a = - 1$ 时，求曲线 $y = f (x)$ 在点 $(1 ， f (x))$ 处的切线方程.

(2)、若函数 $f (x)$ 在 $(0 ， + ∞)$ 单调递增，求 $a$ 的取值范围.

查看试题解析
18. 已知 $f (x) = l n x$ ，取点 $(a_{1} f (a_{1}))$ 过其曲线 $y = f (x)$ 作切线交 $y$ 轴于 $(0 ， a_{2})$ ，取点 $(a_{2} f (a_{2}))$ 过其曲线 $y = f (x)$ 作切线交 $y$ 轴于 $(0 ， a_{3})$ ，若 $a_{3} > 0$ 则继续，若 $a_{3} \leq 0$ 则停止，以此类推得到数列 ${a_{n}}$ .

(1)、若正整数 $m \geq 2$ ，证明 $a_{m} = l n a_{m - 1} - 1$ ；

(2)、若正整数 $m \geq 2$ ，试比较 $a_{m}$ 与 $a_{m - 1} - 2$ 大小；

(3)、若正整数 $k \geq 3$ ，是否存在 $k$ 使得 $a_{1} ， a_{2} ， a_{3} ⋯ a_{k}$ 依次成等差数列?若存在，求出 $k$ 的所有取值，若不存在，请说明理由.

查看试题解析
19. 函数 $f (x) = \frac{x^{2} + (3 a + 1) x + c}{x + a} (a ， c \in R)$

(1)、当 $a = 0$ 是，是否存在实数 $c$ ，使得 $f (x)$ 为奇函数；

(2)、函数 $f (x)$ 的图像过点 $(1 ， 3)$ ，且 $f (x)$ 的图像与 $x$ 轴负半轴有两个交点，求实数 $a$ 的取值范围.

查看试题解析
20.

(1)、证明：当 $0 < x < 1$ 时， $x - x^{2} < s i n x < x$

(2)、已知函数 $f (x) = c o s a x - l n (1 - x^{2}) ，$ 若 $x = 0$ 是 $f (x)$ 的极大值点，求a的取值范围.

查看试题解析
21. 已知函数 $f (x) = a (e^{x} + a) - x$ .

(1)、讨论 $f (x)$ 的单调性；

(2)、证明：当 $a > 0$ 时， $f (x) > 2 l n a + \frac{3}{2}$ .

查看试题解析
22. 在直角坐标系xOy中，点P到x轴的距离等于点P到点(0， $\frac{1}{2}$ )的距离，记动点P的轨迹为W.

(1)、求W的方程；

(2)、已知矩形ABCD有三个顶点在W上，证明：矩形ABCD的周长大于 $3 \sqrt{3}$ .

查看试题解析