（人教版）2023-2024学年九年级数学上册22.1 二次函数的图像和性质同步分层训练（培优卷）

试卷更新日期：2023-07-15 类型：同步测试

进入出卷网下载

一、选择题

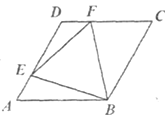
1. 已知菱形ABCD的边长为1，∠DAB=60°，E为AD上的动点，F在CD上，且AE+CF=1，设ΔBEF的面积为y，AE=x，当点E运动时，能正确描述y与x关系的图像是：（）

A、 B、 C、 D、

查看试题解析
2.
如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是( )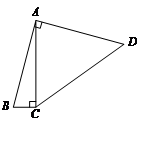

A、 $y = \frac{2}{25} x^{2}$ B、 $y = \frac{4}{25} x^{2}$ C、 $y = \frac{2}{5} x^{2}$ D、 $y = \frac{4}{5} x^{2}$

查看试题解析
3. 函数y=ax²与y=ax+b(a>0，b>0)在同一坐标系中的大致图象是（）

A、 B、 C、 D、

查看试题解析
4. 若二次函数y＝（x﹣3）²+2m，在自变量x满足m≤x≤m+2的情况下，与其对应的函数值y的最小值为5，则m的值为（　　）

A、﹣2或2 B、﹣2或 $\frac{5}{2}$ C、2或 $\frac{5}{2}$ D、﹣2或2或 $\frac{5}{2}$

查看试题解析
5. 已知函数 $y = {\begin{cases} {(x - 1)}^{2} - 1 (x \leq 3) \\ {(x - 5)}^{2} - 1 (x > 3) \end{cases}$ ，则使y=k成立的x值恰好有三个，则k的值为（）

A、0 B、1 C、2 D、3

查看试题解析
6. 点P（x₁ ， y₁），Q（x₂ ， y₂）在抛物线y＝ax²-4ax＋2（a＞0）上，若对于t＜x₁＜t＋1，t＋2＜x₂＜t＋3，都有y₁≠y₂ ，则t的取值范围是（）

A、t≥1 B、t≤0 C、t≥1或t≤0 D、t≥1或t≤-1

查看试题解析
7. 如图，抛物线 $y = a x^{2} + b x + c$ 过点 $(- 1 ， 0)$ ，且对称轴为直线 $x = 1$ ，有下列结论① $a b c < 0$ ；② $10 a + 3 b + c > 0$ ：③抛物线经过点 $(4 ， y_{1})$ 与点 $(- 3 ， y_{2})$ ，则 $y_{1} > y_{2}$ ；④无论a，b，c取何值，抛物线都经过同一个点 $(- \frac{c}{a} ， 0)$ ；⑤ $a m^{2} + b m + a \geq 0$ ，其中正确的结论是（）

A、①②③ B、③④⑤ C、②③④ D、②④⑤

查看试题解析
8. 如图所示，已知二次函数y=ax²+bx+c的图象与x轴交于A、B两点，与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax²+bx+c交于C、D两点，D点在x轴下方且横坐标小于3，则下列结论：
①2a+b+c＞0；②a﹣b+c＜0；③x（ax+b）≤a+b；④a＜﹣1.

其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
9. 如图，是二次函数y=ax²+bx+c（a≠0）的图象的一部分，给出下列命题：
①abc＜0；②b＞2a；③a+b+c=0；④8a+c＞0；⑤ax²+bx+c=0的两根分别为﹣3和1．

其中正确的命题有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
10. 已知当 $－ 1 < x < 0$ 时，二次函数 $y = x^{2} - 4 k x + 3$ 的值恒大于1，则k的取值范围是（）

A、k≥ $- \frac{3}{4}$ B、－ $\frac{3}{4}$ ≤k≤－ $\frac{1}{2}$ C、－ $\frac{1}{2}$ ＜k＜0 D、－ $\frac{3}{4}$ ≤k＜0

查看试题解析

二、填空题

11. 已知 $M (x_{1} ， y_{1})$ ， $N (x_{2} ， y_{2})$ 为抛物线 $y = a x^{2}$ （ $a \neq 0$ ）上任意两点，其中 $0 \leq x_{1} < x_{2}$ ．若对于 $x_{2} - x_{1} = 1$ ，都有 $| y_{2} - y_{1} | \geq 1$ ，则a的取值范围是．

查看试题解析
12. 已知函数y＝ ${\begin{array}{l} - {(x - 1)}^{2} + 1 (x ⩽ 4) \\ - {(x - 7)}^{2} + 1 (x > 4) \end{array}$ ，且使y＝k成立的x值恰好有2个，则k的取值范是．

查看试题解析
13. 如图，在平面直角坐标系中，抛物线 $y = - x^{2} + 4 x$ 的顶点为A ，与x轴分别交于O、B两点．过顶点A分别作AC⊥x轴于点C ， AD⊥y轴于点D ，连结BD ，交AC于点E ，则△ADE与△BCE的面积和为．

查看试题解析
14. 如图，在平面直角坐标系xOy中，抛物线y＝-x²+6x+c的对称轴与x轴交于点A，在直线AB：y＝kx+3上取一点B，使点B在第四象限，且到两坐标轴的距离和为7，设P是抛物线的对称轴上的一点，点Q在抛物线上，若以点A，B，P，Q为顶点的四边形为正方形，则c的值为．

查看试题解析
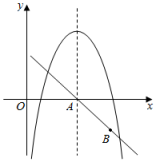15. 如图，正方形ABCD的边长为2，E为边AD上一动点，连接CE，以CE为边向右侧作正方形CEFG，连接DF，DG，则 $△ D F G$ 面积的最小值为．

查看试题解析

三、解答题

16. 在平面直角坐标系中，点 $O (0 ， 0)$ ，点 $A (1 ， 0)$ .已知抛物线 $y = x^{2} + m x - 2 m$ （ $m$ 是常数），顶点为 $P$ .
（Ⅰ）当抛物线经过点 $A$ 时，求顶点 $P$ 的坐标；

（Ⅱ）若点 $P$ 在 $x$ 轴下方，当 $∠ A O P = 45 °$ 时，求抛物线的解析式；

（Ⅲ）无论 $m$ 取何值，该抛物线都经过定点 $H$ .当 $∠ A H P = 45 °$ 时，求抛物线的解析式.

查看试题解析
17. 复习课中，教师给出关于x的函数 $y = 2 k x^{2} - (4 k + 1) x - k + 1$ （k是实数）.
教师：请独立思考，并把探索发现的与该函数有关的结论（性质）写到黑板上.

学生思考后，黑板上出现了一些结论.教师作为活动一员，又补充一些结论，并从中选择如下四条：

①存在函数，其图像经过（1，0）点；

②函数图象与坐标轴总有三个不同的交点；

③当 $x > 1$ 时，不是y随x的增大而增大就是y随x的增大而减小；

④若函数有最大值，则最大值必为正数，若函数有最小值，则最小值必为负数；

教师：请你分别判断四条结论的真假，并给出理由，最后简单写出解决问题时所用的数学方法.

查看试题解析
18. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，根据图象解答下列问题：

(1)、写出不等式 $a x^{2} + b x + c > 0$ 的解集；

(2)、当 $- 1 \leq x \leq 2$ 时，写出函数值y的取值范围。

(3)、若方程 $a x^{2} + b x + c = k$ 有两个不相等的正实数根，写出 $k$ 的取值范围。

查看试题解析

四、综合题

19. 如图，直线 $y = k x + 3$ 交x轴于A点，交y轴于B点，过A、B两点的抛物线的顶点坐标(1，4)．

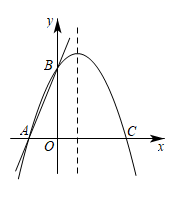
(1)、求k的值和抛物线的解析式；

(2)、在抛物线的对称轴上求一点P ，使得 $△$ PAB的周长最小，并求出最小值；

(3)、在抛物线的对称轴上是否存在点Q ，使 $△$ ABQ是等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．

查看试题解析
20. 已知二次函数图象的顶点为（3，﹣1），与y轴交于点（0，﹣4）．

(1)、求二次函数解析式；

(2)、求函数值y＞﹣4时，自变量x的取值范围．

查看试题解析
21. 在平面直角坐标系中，二次函数 $y = x^{2} - 2 m x + 6 m$ （ $x \leq 2 m$ ， m为常数）的图象记作G，图象G上点A的横坐标为2m．

(1)、当 $m = 1$ ，求图象G的最低点坐标；

(2)、平面内有点 $C (- 2 ， 2)$ ．当AC不与坐标轴平行时，以AC为对角线构造矩形ABCD，AB与x轴平行，BC与y轴平行．
①若矩形ABCD为正方形时，求点A坐标；
②图象G与矩形ABCD的边有两个公共点时，求m的取值范围．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + b x - \frac{1}{a}$ 与 $y$ 轴交于点 $A$ ，将点 $A$ 向右平移 $2$ 个单位长度，得到点 $B$ ，点 $B$ 在抛物线上。

(1)、求点 $B$ 的坐标 $($ 用含 $a$ 的式子表示 $)$ ；

(2)、求抛物线的对称轴；

(3)、已知点P( $\frac{1}{2}$ ， $- \frac{1}{a}$ )， $Q (2 ， 2)$ ，若抛物线与线段 $P Q$ 恰有一个公共点，结合函数图象，求 $a$ 的取值范围．

查看试题解析

（人教版）2023-2024学年九年级数学上册22.1 二次函数的图像和性质 同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年九年级数学上册22.1 二次函数的图像和性质同步分层训练（培优卷）