（人教版）2023-2024学年九年级数学上册22.1 二次函数的图像和性质同步分层训练（基础卷）

试卷更新日期：2023-07-15 类型：同步测试

进入出卷网下载

一、选择题

1. 下列各式中，y是x的二次函数的是（）

A、 $y = 3 x - 1$ B、 $y = \frac{1}{x^{2}}$ C、 $y = 3 x^{2} + x - 1$ D、 $y = 2 x^{3} - 1$

查看试题解析
2. 已知抛物线 $y = a x^{2} （ a \neq 0 ）$ 的开口向下，则a的值可能为（）

A、-2 B、 $\frac{1}{4}$ C、1 D、 $\sqrt{2}$

查看试题解析
3. 若在同一平面直角坐标系中，作y＝3x² ， y＝x²﹣2，y＝﹣2x²+1的图象，则它们（）

A、开口方向相同 B、互相可以通过平移得到 C、都经过原点 D、都关于y轴对称

查看试题解析
4. 二次函数y=x²的图象经过的象限是（）

A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限

查看试题解析
5. 在下列二次函数中，图象的开口向下，顶点坐标为（－2，－1）的是（）

A、 $y = (x - 2)^{2} + 1$ B、 $y = - (x - 2)^{2} - 1$ C、 $y = (x + 2)^{2} + 1$ D、 $y = - (x + 2)^{2} - 1$

查看试题解析
6. 抛物线 $y = 3 (x + 6)^{2} + 3$ 的顶点坐标是（）

A、 $(3 ， 6)$ B、 $(3 ， - 6)$ C、 $(6 ， 3)$ D、 $(- 6 ， 3)$

查看试题解析
7. 下列抛物线中，与抛物线y=2(x-1)²+2形状相同的是（）

A、y= $\frac{1}{2}$ (x-1)² B、y=2x² C、y=(x-1)²+2 D、y=(2x-1)²+2

查看试题解析
8. 抛物线 $y = - 3 x^{2} + 6 x - 1$ 的对称轴是（）

A、直线 $x = 2$ B、直线 $x = 1$ C、直线 $x = - 2$ D、直线 $x = - 1$

查看试题解析
9. 将 $y = x^{2} + 6 x + 7$ 进行配方，正确的结果是（）

A、 $y = {(x - 3)}^{2} - 2$ B、 $y = {(x - 3)}^{2} + 2$ C、 $y = {(x + 3)}^{2} - 16$ D、 $y = {(x + 3)}^{2} - 2$

查看试题解析
10. 对于二次函数 $y = x^{2} - 4 x - 1$ 的图象，下列说法错误的是（）

A、开口向上 B、与x轴有两个交点 C、抛物线的顶点坐标是（2，－5） D、当x≥2时，y随x的增大而减小

查看试题解析

二、填空题

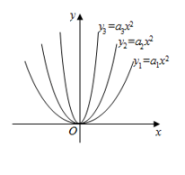
11. 若二次函数 $y = m x^{2} + (2 m + n) x + 3 n$ 的二次项系数比一次项系数小12，一次项系数比常数项大8，则这个二次函数的解析式为.

查看试题解析
12. 在同一个平面直角坐标系中，二次函数 $y_{1} = a_{1} x^{2}$ ， $y_{2} = a_{2} x^{2}$ ， $y_{3} = a_{3} x^{2}$ 的图象如图2所示，则 $a_{1}$ ， $a_{2}$ ， $a_{3}$ 的大小关系为．

查看试题解析
13. 函数y＝x²﹣5的最小值是．

查看试题解析
14. 抛物线 $y = 2 {(x + 1)}^{2} + 2$ 的顶点坐标是.

查看试题解析
15. 若将二次函数 $y = x^{2} - 2 x + 3$ 配方为 $y = {(x - h)}^{2} + k$ 的形式，则y=。

查看试题解析

三、解答题

16. 当k为何值时，函数 $y = (k - 1) x^{k^{2} + k} + 1$ 为二次函数？

查看试题解析
17. 求二次函数y=﹣2（x﹣3）²﹣5的顶点坐标．

查看试题解析
18. 在同一坐标系内，画出函数y=2x²和y=2（x-1）²+1的图象，并说出它们的相同点和不同点．

查看试题解析
19. 某种爆竹点燃后，其上升高度h（米）和时间t（秒）符合关系式：h＝v₀t﹣ $\frac{1}{2}$ gt²（0＜t＜4），其中g以10米/秒²计算.这种爆竹点燃后以v₀＝20米/秒的初速度上升，问：这种爆竹在地面上点燃后，经过多少时间离地面最远？

查看试题解析

四、综合题

20. 已知函数y=（m²﹣m）x²+（m﹣1）x+2﹣2m．

(1)、若这个函数是二次函数，求m的取值范围．

(2)、若这个函数是一次函数，求m的值．

(3)、这个函数可能是正比例函数吗？为什么？

查看试题解析
21. 在同一个直角坐标系中作出y＝ $\frac{1}{2}$ x² ， y＝ $\frac{1}{2}$ x²－1的图象．

(1)、分别指出它们的开口方向、对称轴以及顶点坐标；

(2)、抛物线y＝ $\frac{1}{2}$ x²－1与抛物线y＝ $\frac{1}{2}$ x²有什么关系？

查看试题解析
22. 求下列函数图象的顶点坐标、开口方向及对称轴。

(1)、 $y = 2 {(x + 1)}^{2}$

(2)、 $y = - 4 {(x - 5)}^{2}$

查看试题解析
23. 求下列二次函数图象的开口方向、顶点坐标和对称轴：

(1)、y=-x²+2x-3

(2)、y= $\frac{1}{2}$ x²-2x+ $\frac{1}{2}$

查看试题解析

（人教版）2023-2024学年九年级数学上册22.1 二次函数的图像和性质 同步分层训练（基础卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年九年级数学上册22.1 二次函数的图像和性质同步分层训练（基础卷）