（人教版）2023-2024学年九年级数学上册21.3 实际问题与一元二次方程同步分层训练（提升卷）

试卷更新日期：2023-07-15 类型：同步测试

进入出卷网下载

一、选择题

1. 我国古代著作《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽.每株脚钱三文足，无钱准与一株椽.”其大意为：现请人代买一批椽，这批椽的价钱为6210文.如果每株椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？设这批椽的数量为x株，则符合题意的方程是（）

A、 $3 (x - 1) x = 6210$ B、 $3 (x - 1) = 6210$ C、 $(3 x - 1) x = 6210$ D、 $3 x = 6210$

查看试题解析
2. 某学校举行篮球对抗赛，有 $x$ 支球队参加，每两队之间比赛一场，共安排了28场比赛，则正确的方程为（）

A、 $\frac{1}{2} x (x - 1) = 28$ B、 $\frac{1}{2} x (x + 1) = 28$ C、 $x (x - 1) = 28$ D、 $x (x + 1) = 28$

查看试题解析
3. 有一个两位数，个位数字与十位数字之和为8，把它的个位数字与十位数字对调，得到一个新数，新数与原数之积为1855，则原两位数是（）

A、35 B、53 C、62 D、35或53

查看试题解析
4. 某种植物的主干长出若干数目的支干，每个支干又长出相同数目的小分支，主干、支干、小分支的总数是111．若设每个支干长出的小分支的个数是x，则下面所列方程正确的是（）

A、 ${(1 + x)}^{2} = 111$ B、 $1 + x + {(x + 1)}^{2} = 111$ C、 $1 + x + x^{2} = 111$ D、 $x + x^{2} = 111$

查看试题解析
5. 某学校要组织一次篮球比赛，赛制为单循环形式（每两队之间都要赛一场），计划安排21场比赛，设参赛队数为x，列方程为（）

A、x（x-1）＝21 B、 $\frac{1}{2}$ x（x-1）＝21 C、2x（x-1）＝21 D、x（x＋1）＝21

查看试题解析
6. 要组织一次排球邀请赛，参赛的每两个队之间比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，设比赛组织者应邀请x个队参赛，则x满足的关系式为（）

A、 $\frac{1}{2}$ x（x+1）=28 B、 $x (x - 1) = 28$ C、 $x (x + 1) = 28$ D、 $\frac{1}{2}$ x（x-1）=28

查看试题解析
7. 对于两个关于x的一元二次方程：F₁：ax²+bx+c＝0，F₂：cx²+bx+a＝0，其中a≠c．给出下列判断：
①若方程F₁有两个相等的实数根，则方程F₂也必有两个相等的实数根；
②若方程F₁有两个异号实根，则方程F₂也必有两个异号实根；
③若3是方程F₁的一个根，则 $\frac{1}{3}$ 必是方程F₂的一个根；
④若这两个方程有一个相同的根，则这个根必是1．
其中，正确的有（　　）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
8. 台山某学校某个宿舍同学毕业时都将自己的照片向全宿舍其他同学各送一张表示留念，全宿舍共送56张照片，设该宿舍共有x名同学，根据题意，列出方程为（）

A、 $x (x + 1) = 56$ B、 $x (x - 1) = 56$ C、 $2 x (x + 1) = 56$ D、 $x (x - 1) = 56 \times 2$

查看试题解析
9. 小亮、小明、小刚三名同学中，小亮的年龄比小明的年龄小2岁，小刚的年龄比小明的年龄大1岁，并且小亮与小刚的年龄的乘积是130.你知道这三名同学的年龄各是多少岁吗？设小明的年龄为x岁，则可列方程为（）

A、 $(x + 2) (x - 1) = 130$ B、 $(x - 2) (x + 1) = 130$ C、 $x (x - 2) = 130$ D、 $x (x + 1) = 130$

查看试题解析
10. 在一次同学聚会上，参加的每个人都与其他人握手一次，共握手95次，设参加这次同学聚会的有x人，可得方程（）

A、x（x﹣1）＝190 B、x（x﹣1）＝380 C、x（x﹣1）＝95 D、（x﹣1）²＝380

查看试题解析

二、填空题

11. 在一次同学聚会上，每两个人之间都互相赠送了一份礼物，若一共送出了 $380$ 份礼物，则参加聚会的同学的人数是.

查看试题解析
12. 两个相邻偶数a，b（a＞0，b＞0）的积是168，这两个偶数的和为.

查看试题解析
13. 某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是13，则每个支干长出个小分支.

查看试题解析
14. 学校秋季运动会上，九年级准备队列表演，一开始排成8行12列，后来又有84名同学积极参加，使得队列增加的行数比增加的列数多1．现在队列表演时的列数是．

查看试题解析
15. 有x支球队参加篮球比赛，共比赛21场，每两个队之间只比赛一场，则关于x的方程是．

查看试题解析

三、解答题

16. 我们知道，传销能扰乱一个地方正常的经济秩序，是国家法律明令禁止的．某非法传销组织现有一名头目计划每人发展若干数目的下线，每个下线再发展同样数目的下线成员．经过两轮发展后，非法传销组织成员共有57人，间每个人计划发展下线多少人？

查看试题解析
17. 小知识：古希腊的毕达哥拉斯，在2500年前曾经大胆断言，一条线段（AB）的某一短线段（比如AC）与另一长线段（比如BC）之比，如果正好等于另一长线段（比如BC）同整个线段（AB）的比（即 $B C^{2} = A C \cdot A B$ ），那么这样的比例会给人一种美感，后来我们将分割这条线段（AB）的点C称为线段AB的“黄金分割点”.
在主持节目时，主持人站在舞台的黄金分割点处最自然得体，那么在长20米的舞台AB上，主持人从A点到B点走多少米，他的站台最得体？（取 $\sqrt{2}$ ＝1.4， $\sqrt{3}$ ＝1.7， $\sqrt{5}$ ＝2.2）

查看试题解析
18. 如图，A、B、C、D为矩形的4个顶点，AB＝30cm，BC＝21cm，动点P从点B出发，沿BA方向运动，动点Q同时从点C出发，沿CB方向运动，如果点P、Q的运动速度均为1cm/s．经过多长时间P、Q两点之间的距离是15cm？

查看试题解析
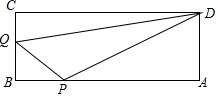19. 某小组要求每两名同学之间都要写评语，小组所有同学一共写了42份评语，这个小组共有学生多少人？

查看试题解析

四、综合题

20. 某校团体操表演队伍有6行8列，后又增加了51人，使得团体操表演队伍增加的行、列数相同，

(1)、求增加了多少行或多少列？

(2)、若团体操表演队在某次文艺汇演，租表演服装每套要50元，化妆每人10元，需支付经费多少元？

查看试题解析
21. 已知关于x的方程x²-(m+1)x+2(m-1)=0，

(1)、求证：无论m取何值时，方程总有实数根；

(2)、若等腰三角形腰长为4，另两边恰好是此方程的根，求此三角形的另外两条边长.

查看试题解析
22. 如图，有长为30m的篱笆，一面利用墙（墙的最大可用长度为10m），围成中间隔有一道篱笆（平行于AB）的长方形花圃．

(1)、设花圃的一边AB为xm，则BC的长可用含x的代数式表示为m；

(2)、当AB的长是多少米时，围成的花圃面积为63平方米？

查看试题解析
23. 如图，四边形 ACDE 是证明勾股定理时用到的一个图形，a 、b 、c 是 Rt△ABC和 Rt△BED 的边长，已知 $A E = \sqrt{2} c$ ，这时我们把关于 x 的形如 $a x^{2} + \sqrt{2} c x + b = 0$ 二次方程称为“勾系一元二次方程”.

请解决下列问题：

(1)、写出一个“勾系一元二次方程”；

(2)、求证：关于 x 的“勾系一元二次方程” $a x^{2} + \sqrt{2} c x + b = 0$ ，必有实数根；

(3)、若 x = -1是“勾系一元二次方程” $a x^{2} + \sqrt{2} c x + b = 0$ 的一个根，且四边形 ACDE 的周长是6 $\sqrt{2}$ ，求△ABC的面积.

查看试题解析

（人教版）2023-2024学年九年级数学上册21.3 实际问题与一元二次方程 同步分层训练（提升卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年九年级数学上册21.3 实际问题与一元二次方程同步分层训练（提升卷）