(人教版)2023-2024学年九年级数学上册21.3 实际问题与一元二次方程 同步分层训练(基础卷)
试卷更新日期:2023-07-15 类型:同步测试
一、选择题
-
1. “绿水青山就是金山银山”,某地为打造绿色产业,实行退耕还林,若计划2022年退耕还林10万公顷,以后退耕还林面积逐年递减,递减率均为10%,那么预计2024年退耕还林的面积为( )A、10万公顷 B、9万公顷 C、8.1万公顷 D、7.29万公顷2. 2022年北京冬奥会女子冰壶比赛,有若干支队伍参加了单循环比赛(每两队之间都赛一场),单循环比赛共进行了45场,共有多少支队伍参加比赛?设共有x支队伍参加比赛,则所列方程为( )A、x(x+1)=45 B、=45 C、x(x-1)=45 D、=453. 在学校举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,某小组成员之间共互赠了30本图书,若设该组共有名同学,那么依题意可列出的方程是( )A、 B、 C、 D、4. 九年(5)班文学小组在举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,全组共互赠了 本图书,如果设全组共有 名同学,依题意,可列出的方程是( )A、 B、 C、 D、5. 一次围棋比赛,参赛的每两位棋手之间都要比赛一场,根据赛程计划共安排45场比赛,设本次比赛共有x个参赛棋手,则可列方程为( )A、 x(x﹣1)=45 B、 x(x+1)=45 C、x(x﹣1)=45 D、x(x+1)=456. 某校九年级学生毕业时,每个同学都将自己的相片向全班其他同学各送一张留作纪念,全班共送了2070张相片,如果全班有x名学生,根据题意,列出方程为( )A、x(x-1)=2070 B、x(x+1)=2070 C、2x(x+1)=2070 D、 =20707. 初三、三班同学在临近毕业时,每一个同学都将自己的照片向全班其他同学各送一张以表示纪念,全班共送了1640张照片,如果设全班有x名学生,则根据题意,可列方程( )A、x(x+1)=1640 B、x(x-1)=1640 C、2x(x+1)=1640 D、x(x-1)=2×16408. 某校九年级(1)班学生毕业时,每个同学都将自己的相片向全班其他同学各送一张留作纪念,全班共送了1980张相片,如果全班有x名学生,根据题意,列出方程为A、 B、x(x+1)=1980 C、2x(x+1)=1980 D、x(x-1)=19809. 某校组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件赛程计划安排7天,每天安排4场比赛,设比赛组织者应邀请x个队参赛,则x满足的关系式是( )A、x(x+1)=28 B、 x(x-1)=28 C、x(x-1)=28 D、2x(x-1)=2810. 如果抛物线y=-x2+2(m-1)x+m+1与x轴交于A、B两点,且A点在x轴正半轴上,B点在x轴的负半轴上,则m的取值范围应是( )A、m>1 B、m>-1 C、m<-1 D、m<1
二、填空题
-
11. 某种植物的主干长出若干数目的枝干,每个枝干又长出同样数目的小分支,主干、支干和小分支的总数是91,那么每个支干长出小分支.12. 某校九(1)班的学生互赠新年贺卡,共用去1560张贺卡,则九(1)班有名学生.13. 某种植物的主干长出若干数目的支干,每个支干又长出同样数量的小分支. 若主干、支干和小分支的总数是 57,设每个支干长出 x 个小分支,则可列方程为14. 有三个连续的自然数,已知其中最大的一个数比另外两个数的积还大1,那么这个最大的数是 .
15. 某种植物的主干长出a个支干,每个支干又长出同样数目的小分支,则主干、支干和小分支的总数为.
三、解答题
-
16. 将一段铁丝围成面积为 的矩形,且它的长比宽多
 ,求矩形的长.
,求矩形的长.
17. 把小圆形场地的半径增加5m得到大圆形场地,大圆形场地面积是小圆形场地的4倍,求小圆形场地的半径.18. 新冠病毒肆虐全球,我国的疫情很快得到了控制,并且研发出安全性、有效性均非常高的疫苗.经调查发现,北京生物制药厂有1条生产线,最大产能是42万支/天,若每增加1条生产线,每条生产线的最大产能将减少2万支/天,现该厂要保证每天生产疫苗144万支,在既增加产能的同时又节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?19. 某校“研学”活动小组在一次野外实践时,发现一种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是43,求这种植物每个支干长出的小分支个数四、综合题
-
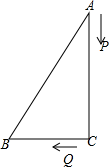
20. 如图,中, , , , , , 是方程的两根.
 (1)、求 , ;(2)、 , 两点分别从 , 出发,分别以每秒2个单位,1个单位的速度沿边 , 向终点 , 运动,(有一个点达到终点则停止运动),求经过多长时间后?21. 某市为鼓励居民节约用水,对居民用水实行阶梯收费,每户居民用水量每月不超过a吨时,每吨按0.3a元缴纳水费;每月超过a吨时,超过部分每吨按0.4a元缴纳水费.(1)、若a=12,某户居民3月份用水量为22吨,则该用户应缴纳水费多少元?(2)、若如表是某户居民4月份和5月份的用水量和缴费情况:
(1)、求 , ;(2)、 , 两点分别从 , 出发,分别以每秒2个单位,1个单位的速度沿边 , 向终点 , 运动,(有一个点达到终点则停止运动),求经过多长时间后?21. 某市为鼓励居民节约用水,对居民用水实行阶梯收费,每户居民用水量每月不超过a吨时,每吨按0.3a元缴纳水费;每月超过a吨时,超过部分每吨按0.4a元缴纳水费.(1)、若a=12,某户居民3月份用水量为22吨,则该用户应缴纳水费多少元?(2)、若如表是某户居民4月份和5月份的用水量和缴费情况:月份
用水量(吨)
交水费总金额(元)
4
18
62
5
24
86
根据上表数据,求规定用水量a的值