（人教版）2023-2024学年九年级数学上册21.2 解一元二次方程同步分层训练（培优卷）

试卷更新日期：2023-07-15 类型：同步测试

进入出卷网下载

一、选择题

1. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0),$ 下列说法：①当 $b = a + c$ 时，则方程 $a x^{2} + b x + c = 0$ 一定有一根为 $x = - 1$ ；②若 $a b > 0 ， b c < 0 ，$ 则方程 $a x^{2} + b x + c = 0$ 一定有两个不相等的实数根；③若c是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ ；④若 $b = 2 a + 3 c$ ，则方程 $a x^{2} + b x + c = 0$ 有两个不相等的实数根．其中正确的是（）

A、①② B、①③ C、①②④ D、②③④

查看试题解析
2. 对于两个不相等的实数 $a ， b$ ，我们规定符号 $max {a ， b}$ 表示 $a ， b$ 中较大的数，如 $\max {2 ， 4} = 4$ ，按这个规定，方程 $\max {x ， - x} = \frac{2 x + 1}{x}$ 的解为（）

A、 $1 - \sqrt{2}$ B、 $2 - \sqrt{2}$ C、 $1 - \sqrt{2} 或 1 + \sqrt{2}$ D、 $1 + \sqrt{2}$ 或-1

查看试题解析
3. 已知菱形ABCD的边长为5，两条对角线交于O点，且OA、OB的长分别是关于 $x$ 的方程 $x^{2} + (2 m - 1) x + m^{2} + 3 = 0$ 的根，则m等于（）

A、 $- 3$ B、 $5$ C、 $5 或 - 3$ D、 $- 5 或 3$

查看试题解析
4. 有两个一元二次方程M：ax²＋bx＋c=0，N：cx²＋bx＋a＝0，其中a·c≠0，a≠c，下列四个结论：① 如果M有两个相等的实数根，那么N也有两个相等实数根；② 如果M与N有实数根，则M有一个根与N的一个根互为倒数；③ 如果M与N有实数根，且有一根相同，那么这个根必是1；④ 如果M的两根符号相同，那么N的两根符号也相同；其中正确的是（）

A、①②③ B、①②④ C、②③④ D、①③④

查看试题解析
5. 关于x的一元二次方程 $x^{2} + 2 m x + 2 n = 0$ 有两个整数根且乘积为正，关于y的一元二次方程 $y^{2} + 2 n y + 2 m = 0$ 同样也有两个整数根且乘积为正．给出四个结论：①这两个方程的根都是负根；② ${(m - 1)}^{2} + {(n - 1)}^{2} \geq 2$ ；③ $- 1 \leq 2 m - 2 n \leq 1$ ．其中正确结论的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
6. 已知α，β是方程x²+2014x+1=0的两个根，则（1+2016α+α²）（1+2016β+β²）的值为（　　）

A、1 B、2 C、3 D、4

查看试题解析
7. 如果关于x的一元二次方程x²﹣4|a|x+4a²﹣1=0的一个根是5，则方程的另一个根是（　　）

A、1 B、5 C、7 D、3或7

查看试题解析
8. 若α、β是方程x²+2x﹣2007=0的两个实数根，则α²+3α+β的值（　　）

A、2007 B、2005 C、﹣2007 D、4010

查看试题解析
9. 用配方法解一元二次方程 $3 x^{2} + 6 x - 1 = 0$ 时，将它化为 ${(x + a)}^{2} = b$ 的形式，则a+b的值为（）

A、 $\frac{10}{3}$ B、 $\frac{7}{3}$ C、2 D、 $\frac{4}{3}$

查看试题解析
10. 已知 $a$ ， $b$ ， $c$ 为常数，点 $P (a ， c)$ 在第四象限，则关于x的一元二次方程 $a x^{2} + b x + c = 0$ 的根的情况为（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法判定

查看试题解析

二、填空题

11. 如图，△ABC中，CD是AB边上的高，AC=8，∠ACD=30°，tan∠ACB= $\frac{5 \sqrt{3}}{3}$ ，点P为CD上一动点，当BP+ $\frac{1}{2}$ CP最小时，DP= ．

查看试题解析
12. 定义：有一组邻边相等的凸四边形叫做等邻边四边形.如图，在Rt△ABC中，∠ABC=90°，AB=2，BC=1，将△ABC沿∠ABC的平分线 $B B'$ 的方向平移，得到△ $A' B' C'$ ，连接 $A C'$ ， $C C'$ ，若四边形 $A B C C'$ 是等邻边四边形，则平移距离 $B B'$ 的长度是.

查看试题解析
13. 若关于x一元二次方程 $(m + 2) x^{2} + 5 x + m^{2} + 3 m + 2 = 0$ 的常数项为0，则m的值等于．

查看试题解析
14. 已知一元二次方程 $x^{2} - 14 x + 48 = 0$ 的两个根是菱形的两条对角线长，则这个菱形的周长．

查看试题解析
15. 已知 $x_{1}$ 、 $x_{2}$ 是方程 $2 x^{2} - 3 x + 1 = 0$ 的两根，则代数式 $\frac{x_{1} + x_{2}}{1 + x_{1} x_{2}}$ 的值为．

查看试题解析

三、解答题

16. 已知△ABC的两边AB、AC的长是关于x的一元二次方程x²－（2k＋3）x＋k²＋3k＋2＝0的两个实数根，第三边BC的长为5，试问：k取何值时，△ABC是以BC为斜边的直角三角形？

查看试题解析
17. 阅读下面的材料，并完成相应的任务．
材料：解含绝对值的方程： $x^{2} - 5 | x | - 6 = 0$ ．

解：分两种情况：

（ 1 ）当 $x \geq 0$ 时，原方程可化为： $x^{2} - 5 x - 6 = 0$ ，解得 $x_{1} = 6$ ， $x_{2} = - 1$ （舍去）；

（ 2 ）当 $x < 0$ 时，原方程可化为： $x^{2} + 5 x - 6 = 0$ ，解得 $x_{1} = - 6$ ， $x_{2} = 1$ （舍去）．

综上所述：原方程的解是 $x_{1} = 6$ ， $x_{2} = - 6$ ．任务：请参照上述方法解方程： $x^{2} - | x | - 2 = 0$ ．

查看试题解析
18. 已知： ABCD的两边AB，AD的长是关于x的方程x²-mx+ $\frac{m}{2}$ - $\frac{1}{4}$ =0的两个实数根．

(1)、当m为何值时，四边形ABCD是菱形?求出这时菱形的边长；

(2)、若AB的长为2，那么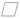 ABCD的周长是多少?

查看试题解析
19. 黄岩某校搬迁后，需要增加教师和学生的寝室数量，寝室有三类，分别为单人间（供一个人住宿），双人间（供两个人住宿），四人间（供四个人住宿）．因实际需要，单人间的数量在20至30之间（包括20和30），且四人间的数量是双人间的5倍．

(1)、若2018年学校寝室数为64个，以后逐年增加，预计2020年寝室数达到121个，求2018至2020年寝室数量的年平均增长率；

(2)、若三类不同的寝室的总数为121个，则最多可供多少师生住宿？

查看试题解析

四、综合题

20. 为了响应国家“自主创业”的号召，某大学毕业生开办了一个装饰品商店，采购了一种今年刚上市的饰品进行了30天的试销，购进价格为20元/件，销售结束后，得知日销售量P（件）与销售时间x（天）之间的关系如图（1）所示，销售价格Q（元/件）与销售时间x（天）之间的关系如图（2）所示．

(1)、根据图象直接写出：日销售量P（件）与销售时间x（天）之间的函数关系式为；销售单价Q（元/件）与销售时间x（天）的函数关系式为．（不要求写出自变量的取值范围）

(2)、写出该商品的日销售利润W（元）和销售时间x（天）之间的函数关系式；（不要求写出自变量的取值范围）

(3)、请问在30天的试销售中，哪一天的日销售利润最大？并求出这个最大利润．

查看试题解析
21. 已知关于x的一元二次方程(a+b)x²+2cx+(b-a)=0，其中a、b、c分别为 $△ A B C$ 三边的长.

(1)、如果 $x = - 1$ 是方程的根，试判断 $△ A B C$ 的形状，并说明理由.

(2)、如果方程有两个相等的实数根，试判断 $△ A B C$ 的形状，并说明理由.

(3)、如果 $△ A B C$ 是等边三角形，试求这个一元二次方程的根.

查看试题解析
22. 矩形ABCD中，M、N为边AD上两点，连接BM、CN，MN=BM=CN，∠BMD=120°。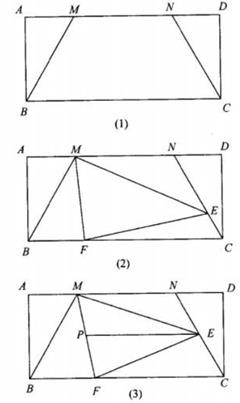

(1)、如图1，求证：AM=DN；

(2)、如图2，点E、F分别在NC、BC上，∠FME=60°，求证：EF"= BF+NE；

(3)、如图3，在(2)的条件下，过E作EP∥BC交MF于P，2MN=3BF，EP=7，求CE的长。

查看试题解析
23. 阅读材料：
材料1 若一元二次方程ax²+bx+c＝0（a≠0）的两个根为x₁ ， x₂则x₁+x₂＝﹣ $\frac{b}{a}$ ，x₁x₂＝ $\frac{c}{a}$ .

材料2 已知实数m，n满足m²﹣m﹣1＝0，n²﹣n﹣1＝0，且m≠n，求 $\frac{n}{m} + \frac{m}{n}$ 的值.

解：由题知m，n是方程x²﹣x﹣1＝0的两个不相等的实数根，根据材料1得m+n＝1，mn＝﹣1，所以 $\frac{n}{m} + \frac{m}{n} = \frac{m^{2} + n^{2}}{m n} = \frac{{(m + n)}^{2} - 2 m n}{m n} = \frac{1 + 2}{- 1}$ ＝﹣3.

根据上述材料解决以下问题：

(1)、材料理解：一元二次方程5x²+10x﹣1＝0的两个根为x₁ ， x₂ ，则x₁+x₂＝， x₁x₂＝.

(2)、类比探究：已知实数m，n满足7m²﹣7m﹣1＝0，7n²﹣7n﹣1＝0，且m≠n，求m²n+mn²的值：

(3)、思维拓展：已知实数s、t分别满足19s²+99s+1＝0，t²+99t+19＝0，且st≠1.求 $\frac{s t + 4 s + 1}{t}$ 的值.

查看试题解析

（人教版）2023-2024学年九年级数学上册21.2 解一元二次方程 同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年九年级数学上册21.2 解一元二次方程同步分层训练（培优卷）