（人教版）2023-2024学年九年级数学上册21.2 解一元二次方程 同步分层训练（基础卷）

试卷更新日期：2023-07-15 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 把方程x2−4x−5=0化成(x+a)2=b的形式，则a、b的值分别是（    ）
    A、2，9 B、2，7 C、-2，9 D、-2，7

    查看试题解析

  • 2. 用配方法解一元二次方程x2−6x=5时，此方程可变形为（　　）
    A、(x+3)2=14 B、(x−3)2=4 C、(x+3)2=9 D、(x−3)2=14

    查看试题解析

  • 3. 一元二次方程（x﹣1）2＝25可以转化为两个一元一次方程，其中一个一元一次方程是x﹣1＝5，则另一个一元一次方程是（  ）
    A、x+1＝﹣5 B、x+1＝5 C、x﹣1＝﹣5 D、x﹣1＝5

    查看试题解析

  • 4. 若关于x的一元二次方程x2−2x+k=0有两个不相等的实数根，则k的值可以是（   ） 
    A、-1 B、1 C、2 D、3

    查看试题解析

  • 5. 一元二次方程有两个不相等的实数根，则（       ）
    A、Δ=0 B、Δ<0 C、Δ>0 D、与Δ的取值无关

    查看试题解析

  • 6. 方程x2+4x+3=0的两个根为（    ）
    A、x1=1 ， x2=3 B、x1=-1 ， x2=3 C、x1=1 ， x2=-3 D、x1=﹣1 ， x2=﹣3

    查看试题解析

  • 7. 解方程4（3x+2）2＝3x+2，较恰当的解法是（  ）
    A、直接开方法 B、因式分解法 C、配方法 D、公式法

    查看试题解析

  • 8. 若x1 ， x2是一元二次方程x2−3x−10=0的两个根.则x1⋅x2的值为（    ）
    A、3 B、10 C、−3 D、−10

    查看试题解析

  • 9. 已知x2+3x−1=0的两个根为x1、x2 ， 则x1+x2的值为（    ）
    A、2 B、－2 C、3 D、－3

    查看试题解析

  • 10. 若α、β是方程x2+2x﹣2017＝0的两个实数根，则α•β的值为（  ）
    A、2017 B、2 C、﹣2 D、﹣2017

    查看试题解析

二、填空题

  • 11. 方程x2+1=2的解是.

    查看试题解析

  • 12. 一元二次方程x2−6x+1=0根的情况为.

    查看试题解析

  • 13. 一个等腰三角形的两条边长分别是方程x2−7x+10=0的两根，则该等腰三角形的周长为.

    查看试题解析

  • 14. 若实数a ， b是一元二次方程x2−3x−1=0的两根，则2a+2b−ab+1=.

    查看试题解析

  • 15. 已知关于x的方程x2+mx−3=0的一个根为x1=1 ， 则方程的另一个根x2= ．

    查看试题解析

三、解答题

  • 16. 已知关于x的一元二次方程（a﹣1）x2﹣2x＋1＝0有两个实数根，求a的非负整数解．

    查看试题解析

  • 17. 若方程（c2＋a2）x2＋2（b2-c2）x＋c2-b2=0有两个相等的实数根，且a，b，c是三角形ABC的三边，证明此三角形是等腰三角形.

    查看试题解析

  • 18. x为何值时，两个代数式x2+1，4x+1的值相等？

    查看试题解析

  • 19. 已知 α , β 是关于x的一元二次方程 x2+(2m+3)x+m2=0 的两个不相等的实数根，且满足 1α + 1β=−1 ，求m的值.

    查看试题解析

四、综合题

  • 20.

    不解方程，求下列方程的两根 的和与积．

    (1)、


    (2)、


    查看试题解析

  • 21. 已知关于x的一元二次方程x2﹣3x+m＝0有两个不相等的实数根x1 ， x2.
    (1)、求m的取值范围.
    (2)、当x1＝5时，求另一个根x2的值.

    查看试题解析

  • 22. 关于x的方程x2﹣2（k﹣1）x+k2＝0有两个实数根x1、x2 ．
    (1)、求k的取值范围；
    (2)、若x1+x2＝1﹣x1x2 ， 求k的值．

    查看试题解析

  • 23.

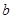    如图所示，在长和宽分别是 、 的矩形纸片的四个角都剪去一个边长为 的正方形．


    (1)、

    用 ， ， 表示纸片剩余部分的面积；

    (2)、

    当 ＝6， ＝4，且剪去部分的面积等于剩余部分的面积时，求剪去的正方形的边长．

    查看试题解析