广东省惠州市惠城区2022-2023学年八年级下册数学期末考试试卷
试卷更新日期:2023-07-14 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 函数中自变量x的可能取值是( )A、 B、 C、 D、2. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、3. 下列四组线段中,可以构成直角三角形的是( )A、1,1,1 B、2,3,4 C、1,2,3 D、5,12,134. 下列运算正确的是( )A、 B、 C、 D、5. 下列函数中,y是x的正比例函数的是( )A、y=5x﹣1 B、y= x C、y=x2 D、y=6. 在“我的中国梦”演讲比赛中,有5名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前3名,不仅要了解自己的成绩,还要了解这5名学生成绩的( )A、中位数 B、众数 C、平均数 D、方差7. 如图,下列哪组条件不能判定四边形ABCD是平行四边形( )
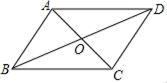 A、AB∥CD , AB=CD B、AB∥CD , AD∥BC C、OA=OC , OB=OD D、AB∥CD , AD=BC8. 在平面直角坐标系xOy中,将直线y=2x+1向上平移2个单位长度后,所得的直线的解析式为( )A、y=2x-1 B、y=2x+2 C、y=2x+3 D、y=2x-29. 如图,在△ABC中,点D、点E分别是AB,AC的中点,点F是DE上一点,且∠AFC=90°,若BC=12,AC=8,则DF的长为( )
A、AB∥CD , AB=CD B、AB∥CD , AD∥BC C、OA=OC , OB=OD D、AB∥CD , AD=BC8. 在平面直角坐标系xOy中,将直线y=2x+1向上平移2个单位长度后,所得的直线的解析式为( )A、y=2x-1 B、y=2x+2 C、y=2x+3 D、y=2x-29. 如图,在△ABC中,点D、点E分别是AB,AC的中点,点F是DE上一点,且∠AFC=90°,若BC=12,AC=8,则DF的长为( ) A、1 B、2 C、3 D、410. 一次函数的图象上有两点A、B , 则的大小关系是( )A、 B、 C、 D、
A、1 B、2 C、3 D、410. 一次函数的图象上有两点A、B , 则的大小关系是( )A、 B、 C、 D、二、填空题(本大题共5小题,每小题3分,共15分)
-
11. = .12. 甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是s甲2=1.2,s乙2=1.1,s丙2=0.6,s丁2=0.9,则射击成绩最稳定的是(填“甲、乙、丙、丁”中的一位).13. 如图,菱形ABCD的边长是4cm,∠ABC=60°,则菱形ABCD的面积为cm2 .
 14. 如图,分别以数轴的单位长度1和3为直角边的长作直角三角形,以数轴上的原点O为圆心,这个直角三角形的斜边长为半径作弧与数轴交于一点A,则点A表示的数为
14. 如图,分别以数轴的单位长度1和3为直角边的长作直角三角形,以数轴上的原点O为圆心,这个直角三角形的斜边长为半径作弧与数轴交于一点A,则点A表示的数为 15. 如图,正方形的边长为2,点是上的动点,以为边在正方形内部作等腰直角三角形 , 连接 , 当点从运动到时,则扫过的面积为
15. 如图,正方形的边长为2,点是上的动点,以为边在正方形内部作等腰直角三角形 , 连接 , 当点从运动到时,则扫过的面积为
三、解答题(一)(本大题共3小题,每小题8分,共24分)
-
16. 计算:17. .如图,点在△ABC中, , , , .
 (1)、求BC的长;(2)、求图中阴影部分的面积.18. 如图是由边长为1的小正方形构成的6×4的网格,点A,B均在格点上.
(1)、求BC的长;(2)、求图中阴影部分的面积.18. 如图是由边长为1的小正方形构成的6×4的网格,点A,B均在格点上.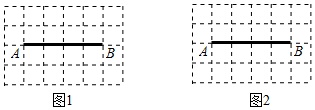
⑴在图1中画出以AB为边且周长为的平行四边形ABCD,且点C和点D均在格点上(画出一个即可);
⑵在图2中画出以AB为对角线的正方形AEBF,且点E和点F均在格点上.
四、解答题(二)(本大题共3小题,每小题9分,共27分)
-
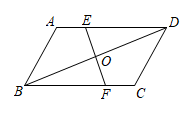
19. 如图,在▱ABCD中,点E、F分别在AD、BC上,且AE=CF,EF、BD相交于点O,求证:OE=OF.
 20. 已知直线y=kx+b经过点A(5,0),B(1,4).
20. 已知直线y=kx+b经过点A(5,0),B(1,4).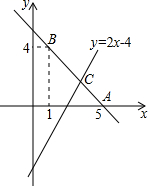 (1)、求直线AB的解析式;(2)、若直线y=2x-4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式 kx+b >2x-的解集.21. 惠城区横沥镇陈大叔承包了甲.乙两座小山,各栽100棵荔枝树,发现成活率均为97%,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的荔枝,每棵的产量如折线统计图所示.
(1)、求直线AB的解析式;(2)、若直线y=2x-4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式 kx+b >2x-的解集.21. 惠城区横沥镇陈大叔承包了甲.乙两座小山,各栽100棵荔枝树,发现成活率均为97%,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的荔枝,每棵的产量如折线统计图所示. (1)、直接写出甲山4棵荔枝树产量的中位数;(2)、分别计算甲、乙两座山荔枝样本的平均数,并判断哪座山的样本的产量高;(3)、用样本平均数估计甲乙两座山荔枝的产量总和.
(1)、直接写出甲山4棵荔枝树产量的中位数;(2)、分别计算甲、乙两座山荔枝样本的平均数,并判断哪座山的样本的产量高;(3)、用样本平均数估计甲乙两座山荔枝的产量总和.五、解答题(三)(本大题共2小题,每小题12分,共24分)
-
22. 小美奶茶店厂生产A.B两种奶茶,由于地处五湖、六桥、八景而闻名的惠州西湖景区,每天都供不应求.经过数学计算,小美发现A种奶茶每杯生产时间为4分钟,B种奶茶每杯生产时间为1分钟,由于原料和运营时间限制,每天生产的总时间为300分钟.(1)、设A种奶茶生产x杯,B种奶茶生产y杯,则y与x之间的函数关系式y= .(2)、由于A种奶茶比较受顾客青睐,小美决定每天生产A种奶茶不少于73杯,那么不同的生产方案有多少种?并写出每种生产方案.(3)、在(2)情况下,若A种奶茶每杯利润为3元,B种奶茶每杯利润为1元,直接写出小美每天获得的最大利润为 .23. 如图,直线交于点 , 交于点 , 直线上有一个动点 , 当点的纵坐标为时,连接 , 过点作轴,过点作 , 交于点。
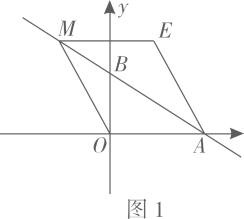
 (1)、求点坐标;(2)、试判断四边形的形状,并说明理由;(3)、点从四边形的顶点出发沿以每秒个单位的速度运动,求的面积与运动时间的函数关系式。
(1)、求点坐标;(2)、试判断四边形的形状,并说明理由;(3)、点从四边形的顶点出发沿以每秒个单位的速度运动,求的面积与运动时间的函数关系式。