浙江省绍兴市新昌县2022-2023学年八年级下册数学期末检测试卷

试卷更新日期：2023-07-14 类型：期末考试

进入出卷网下载

一、选择题（本大题有10小题，每小题3分，共30分．请选出每小题中一个符合题意的正确选项，不选、多选、错选，均不给分）

1. 志愿服务，传递爱心，传递文明，下列志愿服务标志为中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 要使得二次根式 $\sqrt{x - 2}$ 有意义，字母 $x$ 的取值可以是（）

A、 $- 2$ B、0 C、1 D、3

查看试题解析
3. 在反比例函数 $y = \frac{- 2}{x}$ 图象上的点的坐标是（）

A、 $(- 1 ， - 2)$ B、 $(- \frac{1}{2} ， 4)$ C、 $(- 2 ， - 1)$ D、 $(- \frac{1}{2} ， - 4)$

查看试题解析
4. 下列各式计算正确的是（）

A、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ B、 $\sqrt{2} \times \sqrt{5} = \sqrt{7}$ C、 $\sqrt{2} \times \sqrt{5} = \sqrt{10}$ D、 $\sqrt{5} + \sqrt{2} = \sqrt{3}$

查看试题解析
5. 若 $x = 0$ 是方程 $x^{2} - x + m = 0$ 的一个根，则此方程的另一个根是（）

A、 $- 2$ B、0 C、1 D、2

查看试题解析
6. 为考察甲、乙、丙、丁四种小麦的长势，在同一时期分别从中随机抽取部分麦苗，获得苗高（单位： $c m$ ）的平均数与方差分别为： $\bar{x_{甲}} = \bar{x_{丙}} = 13 c m$ ， $\bar{x_{乙}} = \bar{x_{丁}} = 15 c m$ ， $S_{乙}^{2} = S_{丙}^{2} = 3.6 c m^{2}$ ， $S_{甲}^{2} = S_{丁}^{2} = 6.3 c m^{2}$ ，则麦苗又高又整齐的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 已知一个多边形的内角和等于540°，则这个多边形是（）

A、三角形 B、四边形 C、五边形 D、六边形

查看试题解析
8. 在四边形 $A B C D$ 中，已知 $A B ∥ C D$ ，如再加上一个条件，不能判定它是平行四边形的是（）

A、 $A D ∥ B C$ B、 $A B = C D$ C、 $∠ B = ∠ D$ D、 $A C = B D$

查看试题解析
9. 用配方法解一元二次方程ax²+bx+c=0（a≠0），此方程可变形为（）

A、 ${(x + \frac{b}{2 a})}^{2} = \frac{b^{2} - 4 a c}{4 a^{2}}$ B、 ${(x + \frac{b}{2 a})}^{2} = \frac{4 a c - b^{2}}{4 a^{2}}$ C、 ${(x - \frac{b}{2 a})}^{2} = \frac{b^{2} - 4 a c}{4 a^{2}}$ D、 ${(x - \frac{b}{2 a})}^{2} = \frac{4 a c - b^{2}}{4 a^{2}}$

查看试题解析
10. 如图，在矩形 $A B C D$ 中， $A D = 2 A B = 8$ ，对角线 $A C$ 的垂直平分线与边 $A D$ ， $B C$ 分别交于点 $E$ ， $F$ ，则 $E F$ 的长为（）

A、 $\sqrt{5}$ B、 $2 \sqrt{5}$ C、 $\frac{8}{3} \sqrt{3}$ D、5

查看试题解析

二、填空题（本大题有6小题，每小题3分，共18分．）

11. $- 3$ 的相反数是.

查看试题解析
12. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x + m = 0$ 有两个相等的实数根，则 $m$ 的值为．

查看试题解析
13. 某校举办广播体操比赛，评分项目包括精神面貌、整齐程度、动作规范这三项，这三项在总分中所占的比例分别为20%，50%，30%，已知八（1）班在比赛中三项得分依次是8分，9分，10分，则八（1）班这次比赛的总成绩为分．

查看试题解析
14. 如图，在平行四边形 $A B C D$ 中， $∠ A = 45 °$ ， $B C = 2$ ，则 $A B$ 与 $C D$ 之间的距离为．

查看试题解析
15. 已知点 $A (1 ， y_{1})$ ， $B (2 ， y_{2})$ ， $C (- 2 ， y_{3})$ 都在反比例函数 $y = \frac{k}{x}$ （ $k < 0$ ）的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 之间的大小关系为．（请用“＜”连接）

查看试题解析
16. 在一张边长为 $4 c m$ 的正方形纸片上剪下一个一边长为 $5 c m$ 的等腰三角形，要求：等腰三角形的三个顶点都落在正方形的边上，且其中一个顶点与正方形的顶点重合，则所的等腰三角形的面积可能是 $c m^{2}$ （写出至少三个）

查看试题解析

三、解答题（本大题共有8题，第17～18题每题5分，第19～22题每题6分，第23题8分，第24题10分，共52分．解答需写出必要的文字说明、演算步骤或证明过程．）

17. 计算：

(1)、 $\sqrt{48} \div \sqrt{3}$

(2)、 $(2 - \sqrt{2}) (3 + 2 \sqrt{2})$

查看试题解析
18. 解方程：

(1)、 $x^{2} - 9 = 0$

(2)、 $x^{2} - 2 x = 1$

查看试题解析
19. 某工厂车问共有10名工人，调查每个工人的日均生产件数，获得数据如下表：
日均生产件数（件）
10
11
12
13
14
15
人数
1
1
5
1
1
1

(1)、求这10名工人日均生产件数的众数、中位数、平均数．

(2)、若要使80%的工人都能完成任务，应选什么统计量（平均数、中位数、众数）作为日生产件数的定额？并说明理由．

查看试题解析
20. 随着科技水平的提高，电子产品的价格呈下降趋势．某款手机首发日价格为3000元，两个月之后价格为2430元，求这款手机的价格在两个月中平均每月下降的百分率．

查看试题解析
21. 如图，四边形 $A B C D$ 各边的中点分别是 $E$ ， $F$ ， $G$ ， $H$ ，四边形 $E F G H$ 是菱形，且 $A B ⊥ A C$ ．

(1)、求证： $A C = B D$ ．

(2)、已知 $A B = 3$ ， $B C = 5$ ，求菱形 $E F G H$ 的周长．

查看试题解析
22. 在学习多边形的相关知识时，小张同学和小王同学对老师布置“探究多边形的对角线条数”的作业很盛兴趣，小张同学探究得到了 $n$ 边形的对角线条数的公式，并通过上网查证自己探究的结论是正确的．下图是两位同学进行交流的情景．

小王同学把哪个多边形对角线的条数数错了？请你通过计算或者画图来说明．

查看试题解析
23. 如图1，两张纸片正方形 $A B C D$ 与正方形 $B E F G$ 拼在一起，在 $A B$ 边上取 $A M = B E$ ，沿 $D M$ ， $M F$ 分别剪一刀，将 $△ D A M$ 拼至 $△ D C N$ ， $△ M E F$ 拼至 $△ N G F$ ，无缝隙无重叠，如图2．

(1)、求证： $D M = M F$ ．

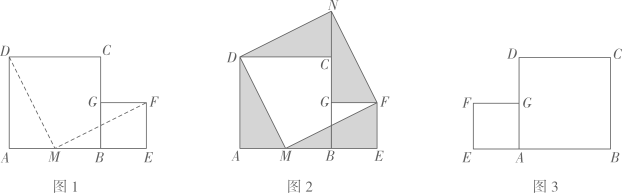(2)、求证：四边形 $D M F N$ 是正方形．

(3)、仿照题中的剪拼方法，剪两刀把图3中两个正方形剪拼成一个更大的正方形，在图中作出剪拼线，并完成拼图．

查看试题解析
24. 如图，过原点的直线 $l$ 交双曲线 $y = \frac{k}{x}$ 于点 $A$ 和点 $B$ ，点 $A$ 的坐标为 $(2 ， 3)$ ，点 $C$ 是双曲线上异于点 $A$ 的动点，且点 $C$ 在第一象限，作直线 $O C$ 交双曲线于点 $D$ ．连结 $A D$ ， $D B$ ， $B C$ ， $C A$ ．

(1)、以下是小明同学探究四边形 $A D B C$ 是平行四边形的过程，请你补充完整：
∵双曲线 $y = \frac{k}{x}$ 关于原点成中心对称，且过原点的直线 $l$ 与双曲线交于点 $A$ 和点 $B$ ，

∴ ．

同理 $O C = O D$ ．

∴四边形 $A D B C$ 是平行四边形．

(2)、问题探究：
① $▱ A D B C$ 是否可能为矩形？请说明理由．
② $▱ A D B C$ 是否可能为菱形？请说明理由．

(3)、当 $▱ A D B C$ 的面积为18时，求点 $C$ 的坐标．

查看试题解析

日均生产件数（件）	10	11	12	13	14	15
人数	1	1	5	1	1	1