广东省肇庆市封开县2022-2023学年七年级下册数学期末考试试卷
试卷更新日期:2023-07-14 类型:期末考试
一、选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的,请把正确选项涂在答题卡上.
-
1. 在 , 0, , 2这四个实数中,最大的数是( )A、0 B、 C、2 D、2. 点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 估计12的算术平方根介于( )A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间4. 方程组的解是( )A、 B、 C、 D、5. 不等式的解集在数轴上表示正确的是( )A、
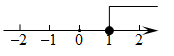 B、
B、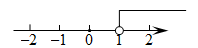 C、
C、 D、
D、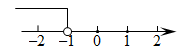 6. 下列命题中,真命题是( )A、4的平方根是2 B、同旁内角互补 C、同位角相等,两直线平行 D、0没有立方根7. 如图, , 射线交于点 , , 则的度数是( )
6. 下列命题中,真命题是( )A、4的平方根是2 B、同旁内角互补 C、同位角相等,两直线平行 D、0没有立方根7. 如图, , 射线交于点 , , 则的度数是( ) A、 B、 C、 D、8. 如图,平分 , 若 , 则( )
A、 B、 C、 D、8. 如图,平分 , 若 , 则( ) A、 B、 C、 D、9. 下列说法正确的是( )A、为了解人造卫星的设备零件的质量情况,应选择抽样调查 B、购买一张体育彩票中奖是不可能事件 C、了解九年级(1)班同学的视力情况,应选择全面调查 D、抛郑一枚质地均匀的硬币刚好正面朝上是必然事件10. 如图, , 为上一点, , 且平分 , 过点作于点 , 且 , 则下列结论:
A、 B、 C、 D、9. 下列说法正确的是( )A、为了解人造卫星的设备零件的质量情况,应选择抽样调查 B、购买一张体育彩票中奖是不可能事件 C、了解九年级(1)班同学的视力情况,应选择全面调查 D、抛郑一枚质地均匀的硬币刚好正面朝上是必然事件10. 如图, , 为上一点, , 且平分 , 过点作于点 , 且 , 则下列结论:①;②;③平分;④平分 . 其中正确的是( )
 A、①② B、①②③ C、②③④ D、①②③④
A、①② B、①②③ C、②③④ D、①②③④二、填空题(本大题5小题,每小题3分,共15分)请将下列各题的正确答案填写在答题卡相应的位置上.
-
11. 计算: = .12. 比较大小: . (填“>”、“<"或“=")13. 如图,直线AB与直线CD相交于点O, , 则 .
 14. 已知和是二元一次方程的两个解,则 .15. 如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFG=65°,则∠2= .
14. 已知和是二元一次方程的两个解,则 .15. 如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFG=65°,则∠2= .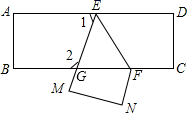
三、解答题(一)(本大题3小题,每小题8分,共24分)
-
16. 计算: .17. 如图
 (1)、写出平面直角坐标系内点M,N,L,P的坐标.(2)、在平面直角坐标系内描出点、、、 .18. 如图.已知 , 垂足为点 , , 垂足为点 , . 请填写的理由.
(1)、写出平面直角坐标系内点M,N,L,P的坐标.(2)、在平面直角坐标系内描出点、、、 .18. 如图.已知 , 垂足为点 , , 垂足为点 , . 请填写的理由.
, , , , (垂直的定义)
,
▲ ( )
, ( )
(已知)
▲ ( ),
▲ ( ),
( )
四、解答题(二)(本大题3小题,每小题9分,共27分)
-
19. 解不等式组 , 把它的解集在数轴上表示出来,并写出其整数解.20. 某市举办“创建全国文明城市”知识竞赛,已知购买一件甲种奖品和2件乙种奖品共需220元,购买2件甲种奖品和3件乙种奖品共需360元.(1)、求每件甲种奖品和每件乙种奖品的价格分别为多少元?(2)、若计划购买甲种奖品和乙种奖品共30件,总费用不多于2300元,那么最少可购买甲种奖品多少件?21. 某校开展了“文明城市”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题活动,每个学生限选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下图所示的不完整的条形统计图和扇形统计图.
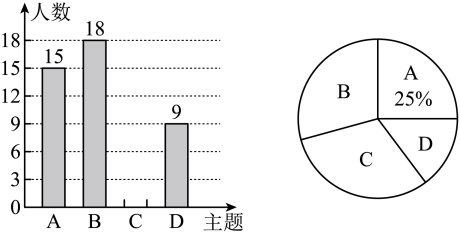 (1)、本次随机调查的学生人数是人;(2)、补全条形统计图;(3)、在扇形统计图中,“B”主题对应扇形的圆心角为度;(4)、若该校共有名学生,试估计该校参与“生态环境”主题的学生人数.
(1)、本次随机调查的学生人数是人;(2)、补全条形统计图;(3)、在扇形统计图中,“B”主题对应扇形的圆心角为度;(4)、若该校共有名学生,试估计该校参与“生态环境”主题的学生人数.五、解答题(三)(本大题2小题,每小题12分,共24分)

