陕西省榆林市绥德县2022-2023学年七年级下册数学期末监测试卷

试卷更新日期：2023-07-14 类型：期末考试

进入出卷网下载

一、选择题（共8小题，每小题3分，计24分，每小题只有一个选项是符合题意的）

1. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 计算： $- x^{4} \cdot (- x^{5})$ 的结果是（）

A、 $x^{9}$ B、 $- x^{9}$ C、 $x^{20}$ D、 $- x^{20}$

查看试题解析
3. 下列事件中，不是必然事件的是（）

A、垂线段最短 B、同位角相等 C、等腰三角形的两个底角相等 D、三角形任意两边之和大于第三边

查看试题解析
4. 如图，在 $△ A B C$ 中，BD是 $△ A B C$ 的中线，BE是 $△ A B D$ 的中线．若 $A E = 3$ ，则AC的长度为（）

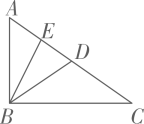A、3 B、6 C、9 D、12

查看试题解析
5. 一副直角三角板按如图所示的方式放置，点E在边BC的延长线上， $B E ∥ D F$ ， $∠ B = ∠ D E F = 90 °$ ，则 $∠ C D E$ 的度数为（）

A、30° B、25° C、20° D、15°

查看试题解析
6. 已知 $a b = 7$ ， $a - b = 5$ ，则 $a^{2} + b^{2}$ 的值为（）

A、39 B、23 C、18 D、9

查看试题解析

7. 一根高18厘米的蜡烛点燃后剩余的高度h（厘米）与燃烧时间t（时）

(0 \leq t \leq 6)

的关系如下表．已知平均每小时蜡烛燃掉3厘米，则蜡烛点燃后剩余的高度h（厘米）与燃烧时间t（时）

(0 \leq t \leq 6)

之间的关系式是（）

燃烧时间t（时）	0	1	2	3	4
剩余的高度h（厘米）	18	15	12	9	6

A、

h = 18 - t

B、

h = 18 + t

C、

h = 18 - 3 t

D、

h = 18 + 3 t

查看试题解析

8. 如图，在四边形ABCD中， $A D ∥ B C$ ，若 $∠ D A B$ 的角平分线AE交CD于E，连接BE，且BE平分 $∠ A B C$ ，延长AE交BC的延长线于F．以下结论不正确的是（）

A、 $B C + A D = A B$ B、 $B C = C E$ C、E为CD的中点 D、 $∠ A E B = 90 °$

查看试题解析

二、填空题（共5小题，每小题3分，计15分）

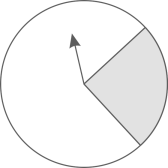
9. 我国自主研发的北斗导航系统的卫星上配置的新一代国产原子钟，其授时精度达到0.000000001秒．将0.000000001用科学记数法表示为．

查看试题解析

10. 如图，某试验小组做了转动转盘，当转盘停止转动后，“指针落在灰色区域内”的试验，试验数据如下表：

试验次数 $n$	20	40	60	80	100	1000
“指针落在灰色区域内”的次数 $m$	6	11	15	21	25	250
“指针落在灰色区域内”的频率 $\frac{m}{n}$	0.3	0.275	0.25	0.2625	0.25	0.25

根据表格，可以估计出转动转盘一次，当转盘停止转动后，“指针落在灰色区域内”的概率是．（精确到百分位）

查看试题解析

11. 已知 $2 x + 5 y + 3 = 0$ ，则 ${(2^{x})}^{2} \cdot {(2^{5})}^{y}$ 的值为．

查看试题解析
12. 如图，在 $∠ M O N$ 中，AB与OM相交于点A，与ON相交于点B， $O P ⊥ A B$ ，垂足为P，添加一个条件，使 $△ A O P ≌ △ B O P$ ．（填一个即可）

查看试题解析
13. 如图，点N是四边形ABCD的DC边上一点，沿BN折叠四边形，使点C落在边AD上的点M处，再沿BM，NM折叠这个四边形，若点A，D恰好同时落在BN上的点P处，则 $∠ M B N$ 的度数为°．

查看试题解析

三、解答题（共13小题，计81分．解答应写出过程）

14. 计算： ${(3.14 - 5)}^{0} + 3^{3} \div 3 - {(- \frac{1}{3})}^{- 2}$ ．

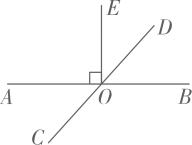
查看试题解析
15. 如图，直线AB，CD相交于点O， $O E ⊥ A B$ ，垂足为O．若 $∠ E O D = 42 °$ ，求 $∠ A O C$ 和 $∠ C O B$ 的度数．

查看试题解析
16. 化简： $(2 x + 1) (2 x - 1) - (8 x^{3} - 4 x^{2}) \div 2 x$ ．

查看试题解析
17. 如图，在四边形ABDC中， $∠ C = 90 °$ ，连接AD，且AD平分 $∠ C A B$ ，过点D作 $D E ⊥ A B$ 于点E．若 $C D = 6$ ， $A E = 8$ ，求四边形ACDE的面积．

查看试题解析
18. 如图，以直线l为对称轴，画出轴对称图形的另一半．

查看试题解析
19. 如图，已知 $△ A B C$ ，利用尺规作 $∠ B A C$ 的平分线AD交BC于点D．（保留作图痕迹，不写作法）

查看试题解析
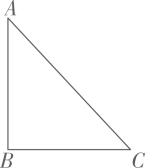20. 如图，AD、AE分别为 $△ A B C$ 的高线和角平分线， $∠ B = 30 °$ ， $∠ A C D = 50 °$ ，求 $∠ E A D$ 的度数．

查看试题解析
21. 奇思利用一根长3m的竿子来测量电线杆AB的高度．他的方法如下：如图，在电线杆前选一点P，使 $B P = 3 m$ ，并测得 $∠ A P B = 70 °$ ，然后把竖直的竿子 $C D (C D = 3 m)$ 在BP的延长线上左右移动，使 $∠ C P D = 20 °$ ，此时测量 $B D = 11.2 m$ ．已知 $C D ⊥ B D$ ， $A B ⊥ B D$ ，计算出电线杆AB的高度．

查看试题解析
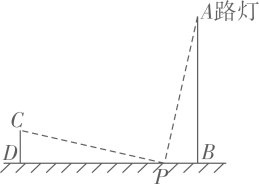22. 笑笑做掷骰子游戏，她掷一枚质地均匀的骰子．

(1)、求笑笑掷出的点数小于1的概率；

(2)、求笑笑掷出的点数是质数的概率；

(3)、求笑笑掷出的点数不小于3的概率．

查看试题解析
23. 大自然中的大部分物质具有热胀冷缩现象，而水则具有反膨胀现象，如图所示是当温度在0℃~15℃时，水的密度 $ρ$ （单位： $k g / m^{3}$ ）随着温度t（单位：℃）的变化关系图象．看图回答问题．

(1)、图中的自变量是什么？因变量是什么？

(2)、图中A点表示的意义是什么？

(3)、当温度在0℃~15℃变化时，水的密度 $ρ$ 是如何变化的？

查看试题解析
24. 如图， $A B ∥ C D$ ，点M、N分别在AB、CD上，连接MN，点P、Q分别在 $∠ A M N$ 、 $∠ D N M$ 的内部，连接MP、PQ、QN，NQ平分 $∠ M N D$ ．

(1)、若 $∠ A M N = 60 °$ ，求 $∠ D N Q$ 的度数；

(2)、若 $∠ P = ∠ Q$ ，试说明MP平分 $∠ A M N$ ．

查看试题解析
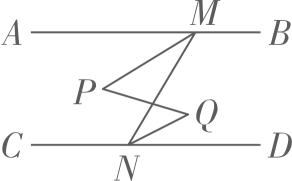25. 如图，在某高铁站广场前有一块长为 $2 a + b$ ，宽为 $a + b$ 的长方形空地，计划在中间留两个长方形喷泉池（图中阴影部分），两个长方形喷泉池及周边留有宽度为b的人行通道．

(1)、求该长方形空地的面积；（用代数式表示）

(2)、求这两个长方形喷泉池的总面积；（用代数式表示）

(3)、当 $a = 200$ ， $b = 100$ 时，求这两个长方形喷泉池的总面积．

查看试题解析
26. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，点D为BC边上一点，E为AC延长线上的一点， $C E = C D$ ， F为CB边上一点，连接EF，延长AD交EF于点K， $E F ⊥ A K$ ，过点D作直线 $D G ⊥ A B$ 于G，延长GD交EF于点H，作 $G M$ 平分 $∠ A G H$ 交AD于点M，过点M作 $M N ∥ A B$ 交EF于点N，交GD于点O，交BC于点Q， $M O = N O$ ，连接GN．

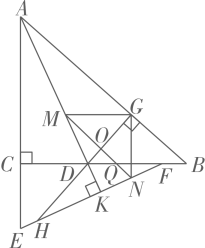(1)、 $∠ D H K$ 与 $∠ B A K$ 相等吗？为什么？

(2)、试说明 $M D = E H + N F$ ．

查看试题解析