陕西省渭南市潼关县2022-2023学年七年级下册数学期末检测试卷

试卷更新日期：2023-07-14 类型：期末考试

进入出卷网下载

一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是符合题意的）

1. 下列调查中最适合用全面调查的方式是（）

A、了解来西安游客满意度调查 B、乘坐地铁时进站安检 C、了解黄河内现有鱼的种类 D、某批次灯泡的平均使用寿命

查看试题解析
2. 若 $a > b$ ，则 $- 2 a □ - 2 b$ ， “ $□$ ”中应填的符号是（）

A、< B、> C、 $\geq$ D、=

查看试题解析
3. 如图，三角板的直角顶点落在长方形纸片的一边上．若 $∠ 1 = 42 °$ ，则 $∠ 2$ 的度数是（）

A、84° B、58° C、48° D、42°

查看试题解析
4. 如图是丁丁画的一张脸的示意图，如果用（0，2）和（2，2）分别表示左、右眼睛，那么嘴的位置可以表示成（）

A、（l，0） B、 $(- 1 ， 0)$ C、 $(- 1 ， 1)$ D、 $(1 ， - 1)$

查看试题解析
5. 如图，已知BF，CD相交于点O， $∠ D = 40 °$ ，下列说法正确的是（）

A、当 $∠ C = 40 °$ 时， $A B ∥ C D$ B、当 $∠ B = 40 °$ 时， $A C ∥ D E$ C、当 $∠ E = 120 °$ 时， $C D ∥ E F$ D、当 $∠ B O C = 140 °$ 时， $B F ∥ D E$

查看试题解析
6. 给出下面一组数据：19，20，25，31，28，27，26，21，20，22，24，23，25，29，27，28，27，30，18，20．若组距为2，则这组数据的组数为（）

A、4 B、5 C、6 D、7

查看试题解析
7. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} 4 x + 3 y = 1 \\ (k - 1) x + 3 k y = 3 \end{array}$ 的解中 $x$ 与 $y$ 互为相反数，则 $k$ 的值为（）

A、2 B、0 C、 $- 2$ D、 $- 4$

查看试题解析
8. 若关于 $x$ 的不等式组 ${\begin{array}{l} 3 x - 2 < 1 \\ m - x < 1 \end{array}$ ，恰有两个整数解，则m的取值范围是（）

A、 $- 1 < m \leq 0$ B、 $- 1 \leq m < 0$ C、 $- 1 < m < 0$ D、 $- 1 < m \leq 1$

查看试题解析

二、填空题（共5小题，每小题3分，计15分）

9. 双减政策下，为了解某学校七年级1260名学生的睡眠情况，抽查了其中200名学生的睡眠时间进行统计，则本次抽样调查的样本容量是．

查看试题解析
10. 如图，数轴上A、B两点对应的实数是 $- \sqrt{2}$ 和1，则两点间的距离为．

查看试题解析
11. 《九章算术》是我国古代数学的经典书，书中有一个方程问题：“五只雀、六只燕，共重1斤（等于16两），雀重燕轻．互换其中一只，恰好一样重，问：每只雀、燕的重量各为多少？”设每只雀的重量为 $x$ 两、每只燕的重量为 $y$ 两，可列方程组为．

查看试题解析
12. 当 $x$ 时，式子 $\frac{6 x - 1}{4} - 2 x$ 的值是非正数．

查看试题解析
13. 如图，已知 $A B ∥ C D$ ，直线 $M N$ 分别与直线 $A B$ 、 $C D$ 交于点 $Q$ 、 $E$ ， $Q F$ 平分 $∠ E Q A$ ，交 $C D$ 于点 $F$ ， $F G ⊥ F Q$ 交 $A B$ 于点 $G$ ，若 $∠ M E C = 36 °$ ，则 $∠ G F E =$ ．

查看试题解析

三、解答题（共13小题，计81分．解答应写出过程）

14. 计算： $\sqrt{(- 2)^{2}} + | \sqrt{2} - \sqrt{3} | - | \sqrt{3} - 1 |$ ．

查看试题解析
15. 解方程组： ${\begin{array}{l} 7 x - 3 y = 2 \\ 2 x + y = 8 \end{array}$

查看试题解析
16. 在平面直角坐标系中，点M的坐标为 $(a - 3 ， a + 4)$ ，点N的坐标为 $(\sqrt{5} ， 9)$ ．若 $M N ∥ y$ 轴，求点M的坐标．

查看试题解析
17. 解不等式组 ${\begin{array}{l} 2 (x - 1) < x + 1 ， \\ 1 - \frac{2 x + 5}{3} \leq x ， \end{array}$ 并写出它的正整数解．

查看试题解析
18. 如图，AF与BD相交于点C， $∠ B = ∠ A C B$ ，且CD平分 $∠ E C F$ ．求证： $A B ∥ C E$ ．

查看试题解析
19. 如图，在平面直角坐标系中，A、B、C三点的坐标分别为 $(- 5 ， 4)$ 、 $(- 3 ， 0)$ 、 $(0 ， 2)$ ．

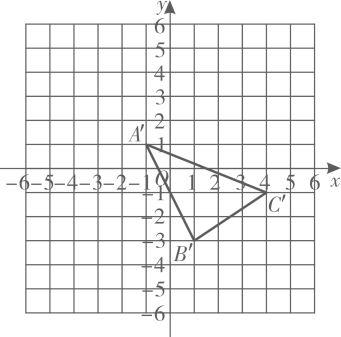(1)、画出三角形ABC；

(2)、如图，三角形 $A^{'} B^{'} C^{'}$ 是由三角形ABC经过平移得到的．已知点 $P (a ， b)$ 为三角形ABC内的一点，则点P在三角形 $A^{'} B^{'} C^{'}$ 内的对应点 $P^{'}$ 的坐标是．

查看试题解析
20. 如图，直线AB，CD相交于点O，已知 $∠ B O C = 75 °$ 、ON将 $∠ A O D$ 成两个角，且 $∠ A O N ： ∠ N O D = 2 ： 3$ ．求 $∠ A O N$ 的度数．

查看试题解析
21. 教育兴则国家兴，教育强则国家强．某校计划增添一批电脑和电子白板，经过市场考察得知，每台电脑0.5万元，每台电子白板1.5万元．根据学校实际，需购进电脑和电子白板共30台，且总费用不超过30万元，该校至少购进电脑多少台？

查看试题解析
22. 已知 $5 x + 2$ 的立方根是3， $3 x + y - 1$ 的算术平方根是4．求 $x + 2 y$ 的平方根．

查看试题解析
23. 为引导广大青少年树立正确的世界观、人生观、价值观，传承红色基因，某校组织480名师生去红色革命圣地-延安开展研学旅行，学校向租车公司租赁A、B两种车型接送师生往返，已知每辆A型车有45个座位，每辆B型车有60个座位．若租车公司最多能提供7辆B型车，且学校两种车型都要租用，没有剩余座位，请问有几种租车方案？并写出符合题意的所有租车方案．

查看试题解析

24. 中国是世界文明发源地之一，是举世闻名的礼仪之邦．一个民族，之所以在世界文明？之林享誉千年，在于它独特而充满魅力的文化．为了弘扬优秀传统文化，某中学举办了传统文化知识大赛（全体同学都参为），其规则是：每位参赛选手回答100道选择题，答对一题得1分，不答或错答得0分，赛后抽取部分参赛选手的答题成绩（单位：分）进行了相关统计，整理并绘制成如下的统计图表：

组别	成绩 $(x)$	频数（人）	百分比
1	$50 \leq x < 60$	30	$a$
2	$60 \leq x < 70$	45	15%
3	$70 \leq x < 80$	60	$b$
4	$80 \leq x < 90$	$m$	40%
5	$90 \leq x \leq 100$	45	15%

请根据以上信息，解答下列问题：

(1)、表中

m =

，

a =

，

b =

；

(2)、补全频数分布直方图；

(3)、如果将其绘制成扇形统计图，请求出参赛成绩不低于90分这组所在扇形圆心角的度数．

查看试题解析

25. 端午节是中国传统节日，人们有吃粽子的习俗．某商场从5月1日起开始打折促销，购买4盒肉粽和5盒红枣粽需440元，购买5盒肉棕和10盒红枣粽需700元．

(1)、每盒肉粽和红枣粽各多少元？

(2)、轩轩想在端午节为敬老院送粽子，他带了1000元钱去该商场买粽子，已知购买的红枣粽比肉棕的2倍多6盒，则他最多可以买多少盒肉棕？

查看试题解析
26. 问题背景
如图，直线 $M N ∥ O B$ ，直角三角板CDE的顶点C，D分别在直线OB，MN上，且 $∠ C E D = 90 °$ ， $∠ D C E = 60 °$ ，设 $∠ A O B = α (0 ° < α < 90 °)$ ．

(1)、问题提出
如图1，若 $C E ∥ O A$ ， $∠ M D C = 110 °$ ，求 $α$ 的度数；

(2)、问题探究
若 $∠ M D C$ 的平分线DF交OB于点F．
①如图2，当 $C E ∥ O A$ ，且 $∠ M D C = 120 °$ 时，求证： $D F ∥ O A$ ；
②如图3，当 $C E ∥ O A$ 保持不变时，试求出 $∠ D F C$ 与 $α$ 之间的数量关系．

查看试题解析