黑龙江省齐齐哈尔市龙沙区2022-2023学年八年级下册数学期末试卷
试卷更新日期:2023-07-14 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 下列式子一定是二次根式是( )A、 B、 C、 D、2. 计算:( )A、 B、 C、 D、3. 如图,在平行四边形中,若 , 则的度数为( )
 A、 B、 C、 D、4. 下列函数是正比例函数的是( )A、 B、 C、 D、5. 一组数据:3,4,5,6,6的中位数是(A、4 B、4.5 C、5 D、66. 如图,网格中的每个小正方形的边长为1,的顶点均在网格的格点上,于点 , 则的长为( )
A、 B、 C、 D、4. 下列函数是正比例函数的是( )A、 B、 C、 D、5. 一组数据:3,4,5,6,6的中位数是(A、4 B、4.5 C、5 D、66. 如图,网格中的每个小正方形的边长为1,的顶点均在网格的格点上,于点 , 则的长为( )
 A、 B、 C、 D、7. 如图,在中, , 点为斜边上的中点,则为( )
A、 B、 C、 D、7. 如图,在中, , 点为斜边上的中点,则为( ) A、10 B、3 C、5 D、48. 一组数据的方差为 , 如果把这组数据中的每个数据都扩大为原来的3倍,那么所得到的一组新数据的方差为( )A、 B、 C、 D、9. 如图,在平面直角坐标系中,正方形的边长为1,边的中点处有一动点 , 动点沿运动一周,则点的纵坐标与点走过的路程之间的函数关系用图象表示大致是( )
A、10 B、3 C、5 D、48. 一组数据的方差为 , 如果把这组数据中的每个数据都扩大为原来的3倍,那么所得到的一组新数据的方差为( )A、 B、 C、 D、9. 如图,在平面直角坐标系中,正方形的边长为1,边的中点处有一动点 , 动点沿运动一周,则点的纵坐标与点走过的路程之间的函数关系用图象表示大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在中, , 于点D,平分 , 且于点E,与交于点F,H是的中点,连接 , 与交于点G.有下列结论:①是等腰三角形;②;③;④ , 其中,正确的有( )
10. 如图,在中, , 于点D,平分 , 且于点E,与交于点F,H是的中点,连接 , 与交于点G.有下列结论:①是等腰三角形;②;③;④ , 其中,正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每通3分,共30分)
-
11. 化简的结果为12. 函数的自变量的取值范围是 .13. 计算的结果等于 .14. 如图,中为的角平分线, .
 15. 已知甲、乙两支篮球队的人数相同,且平均身高都是 , 身高的方差分别是 , , 则身高比较整齐的篮球队是 . (填“甲”或“乙”)16. 如图,在平行四边形中,E,F是对角线上的两点,请添加一个条件 , 使四边形是平行四边形(填一个即可)
15. 已知甲、乙两支篮球队的人数相同,且平均身高都是 , 身高的方差分别是 , , 则身高比较整齐的篮球队是 . (填“甲”或“乙”)16. 如图,在平行四边形中,E,F是对角线上的两点,请添加一个条件 , 使四边形是平行四边形(填一个即可)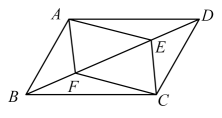 17. 如图,已知菱形的边长为 , , 为的中点,若为对角线上一动点,则的最小值为.
17. 如图,已知菱形的边长为 , , 为的中点,若为对角线上一动点,则的最小值为.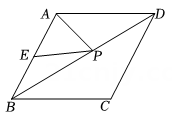 18. 平面直角坐标系中,直线上有一点A,已知点A的横坐标等于2,经过点A的直线与轴夹角等于 , 与轴交于点 , 则点坐标为19. 如图,在矩形中,是边上的中点,是边上的一动点.连接 , 特沿折叠,点的对应点为点 , 连接 . 当为直角三角形时,的长为 .
18. 平面直角坐标系中,直线上有一点A,已知点A的横坐标等于2,经过点A的直线与轴夹角等于 , 与轴交于点 , 则点坐标为19. 如图,在矩形中,是边上的中点,是边上的一动点.连接 , 特沿折叠,点的对应点为点 , 连接 . 当为直角三角形时,的长为 .
 20. 如图,在平面直角坐标系中,直线交轴于点 , 交轴于点 , 且在直线上,点在轴的正半轴上, , 依次均为等腰直角三角形,直角顶点都在轴上,则点的横坐标为 .
20. 如图,在平面直角坐标系中,直线交轴于点 , 交轴于点 , 且在直线上,点在轴的正半轴上, , 依次均为等腰直角三角形,直角顶点都在轴上,则点的横坐标为 .
三、解答题(共60分)
-
21. 计算: .22. 为了了解某校初中各年级学生每天的平均睡眠时间(单位:h,精确),抽样调查了部分学生,并用得到的数据绘制了下而两幅不完整的统计图。
请你根据图中提供的信息,回答下列问题:
 (1)、求出扇形统计图中百分数a的值为 , 所抽查的学生人数为 .(2)、求出平均睡眠时间为8小时的人数,并补全条形图.(3)、求出这部分学生的平均睡眠时间的众数和平均数.(4)、如果该校共有学生1200名,请你估计睡眠不足((少于8小时)的学生数.23. 计划将甲、乙两厂的生产设备运往A,B两地,甲厂设备有60台,乙厂设备有40台,A地需70台,B地需30台,每台设备的运输费(单位:百元)如表格所示,设从甲厂运往A地的有x台设备(x为整数).
(1)、求出扇形统计图中百分数a的值为 , 所抽查的学生人数为 .(2)、求出平均睡眠时间为8小时的人数,并补全条形图.(3)、求出这部分学生的平均睡眠时间的众数和平均数.(4)、如果该校共有学生1200名,请你估计睡眠不足((少于8小时)的学生数.23. 计划将甲、乙两厂的生产设备运往A,B两地,甲厂设备有60台,乙厂设备有40台,A地需70台,B地需30台,每台设备的运输费(单位:百元)如表格所示,设从甲厂运往A地的有x台设备(x为整数).A地
B地
甲厂
7
10
乙厂
10
15
(1)、用含x的式子直接填空:甲厂运往B地台,乙厂运往A地台,乙厂运往B地台.(2)、请你设计一种调运的运输方案,使总费用最低,并求出最低费用为多少?(3)、因客观原因,从甲到A的运输费用每台增加了m百元,从乙到B的运输费用每台减小了百元,其它不变,若要使费用最低的调运方案不变,请直接写出m的取值范围。24. 小亮和姐姐周末去体育场观看比赛,姐姐骑共享单车保持匀速从家到体育场,到达赛场后观看比赛用了 , 看完比赛后骑车以同样的速度沿原路返回家中,姐姐从家出发的同时,小亮刚看完上一场比赛从体育场步行返回家中,结果比姐姐早到家,姐姐从家出发开始计时,两人离家的距离y(m)与所用时间t(min)之间的关系图像如图所示,请结合图像信息解答下列问题: (1)、 , ;(2)、求出姐姐从家出发直到返回家的过程中,姐姐离家的距离与时间t之间的关系式;(3)、在姐姐去体育场的过程中,直接写出t为何值时,两人相距 .25. 综合与实践
(1)、 , ;(2)、求出姐姐从家出发直到返回家的过程中,姐姐离家的距离与时间t之间的关系式;(3)、在姐姐去体育场的过程中,直接写出t为何值时,两人相距 .25. 综合与实践 (1)、如图1,正方形的对角线相交于点 , 点又是正方形的一个顶点,而且这两个正方形的边长都为1,四边形为两个正方形重叠部分.正方形可绕点转动.则下列结论正确的是(填序号即可).
(1)、如图1,正方形的对角线相交于点 , 点又是正方形的一个顶点,而且这两个正方形的边长都为1,四边形为两个正方形重叠部分.正方形可绕点转动.则下列结论正确的是(填序号即可).①;②;③四边形的面积总等于;④连接 , 总有 .
(2)、如图2,矩形的对角线中点是矩形的一个顶点,与边相文于点与边相交于点 , 连接 , 矩形可绕着点旋转.①猜想之间的数量关系,并进行证明;
②直接写出线段之间的数量关系为 ▲ .
(3)、如图3,在中, , 直角的顶点在边的中点处,它的两条边和分别与直线相交于点可绕着点旋转,当时,线段的长度为 .26. 综合与探索【探索发现】如图1,等腰直角三角形中, , 过点作交于点 , 过点作交于点 , 易得 , 我们称这种全等模型为“型全等”.(不需要证明)
【迁移应用】如图2,在直角坐标系中,真线分别与轴,轴交于点 ,
 (1)、直接写出 , ;(2)、在第二象限构造等腰直角 , 使得 , 则点的坐标为;(3)、如图3,将直线绕点顺时针旋转得到 , 求的函数表达式;(4)、【拓展应用】
(1)、直接写出 , ;(2)、在第二象限构造等腰直角 , 使得 , 则点的坐标为;(3)、如图3,将直线绕点顺时针旋转得到 , 求的函数表达式;(4)、【拓展应用】如图4,直线分别交轴和轴于两点,点在第二象限内一点,在平面内是否存在一点 , 使以为顶点的四边形为正方形?若存在,请直接写出点的坐标;若不存在,请说明理由.