黑龙江省双鸭山市2022-2023学年八年级下册数学期末试卷

试卷更新日期：2023-07-14 类型：期末考试

进入出卷网下载

一、选择题（每题3分，满分30分）

1. 下列各式计算正确的是（）

A、 $\sqrt{24} \div \sqrt{6} = 4$ B、 $\sqrt{54} \div \sqrt{9} = \sqrt{6}$ C、 $\sqrt{30} \div \sqrt{6} = 5$ D、 $\sqrt{\frac{4}{7}} \div \sqrt{\frac{1}{49}} = 7 \sqrt{2}$

查看试题解析
2. 满足下列条件的 $△ A B C$ ，其中不是直角三角形的是（）

A、 $b^{2} = (a + c) (a - c)$ B、 $a ： b ： c = 1 ： \sqrt{3} ： 2$ C、 $∠ C = ∠ A - ∠ B$ D、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$

查看试题解析

3. 某校男子足球队的年龄分布如下表：

年龄/岁	13	14	15	16	17	18
人数	2	6	8	3	2	1

则这些队员年龄的平均数是（）

A、13 B、14 C、14.5 D、15

查看试题解析

4. 同一平面直角坐标系中，一次函数 $y_{1} = m x + n$ 与 $y_{2} = n x + m$ （m，n为常数）的图象可能是（）

A、 B、 C、 D、

查看试题解析
5. 如图，在正方形ABCD中，E是对角线上一点，连接AE，CE，若 $D E = A B$ ，则 $∠ A E C$ 的度数为（）

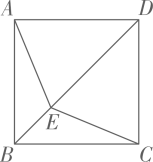A、105° B、120° C、135° D、150°

查看试题解析
6. 我们规定：对于任意的正数m，n的运算“ $Φ$ ”为当 $m < n$ 时， $m Φ n = 2 \sqrt{m} + \sqrt{n}$ ；当 $m \geq n$ 时， $m Φ n = 2 \sqrt{m} - \sqrt{n}$ ，其他运算符号意义不变，按上述规定，计算 $(3 Φ 2) - (8 Φ 12)$ 的结果为（）

A、 $5 \sqrt{2}$ B、 $- 5 \sqrt{2}$ C、 $4 \sqrt{2}$ D、 $- 4 \sqrt{2}$

查看试题解析
7. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，按以下步骤作图：①以点B为圆心，任意长为半径作弧，分别交BA，BC于M，N两点；②分别以点M，N为圆心，以大于 $\frac{1}{2} M N$ 的长为半径作弧，两弧相交于点P；③作射线BP，交边AC于点D.若 $A B = 10$ ， $B C = 6$ ，则线段CD的长为（）

A、3 B、 $\frac{10}{3}$ C、 $\frac{8}{3}$ D、 $\frac{16}{5}$

查看试题解析
8. 数形结合是解决数学问题常用的思想方法.如图，直线y=x+5和直线y=ax+b，相交于点P ，根据图象可知，方程x+5=ax+b的解是（）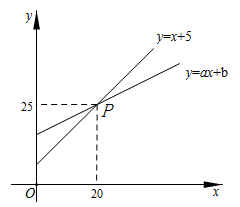

A、x=20 B、x=5 C、x=25 D、x=15

查看试题解析
9. 如图，在△ABC中，D、E分别为AB、AC的中点，CF平分∠ACB，交DE于点F，若AC＝4，则EF的长为（）

A、1 B、2 C、3 D、4

查看试题解析
10. 某市举办中小学生春季越野大赛，小明、小颖两名同学同时从起点出发，他们所跑的路程y（单位：千米）与时间x（单位：分钟）的函数关系如图所示.小刚由图象得出下列信息：①出发后，途中小明和小颖有3次相遇；②小明在比赛中的速度始终比小颖快，所以小明先到达终点；③比赛开始20分钟时小颖跑了2500米；④越野全程为6000米.在小刚得出的信息中，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题3分，满分24分）

11. 在函数 $y = \frac{\sqrt{x + 2}}{x - 3}$ 中，自变量x的取值范围为.

查看试题解析
12. 已知 $x = \sqrt{3} + \sqrt{2}$ ， $y = \sqrt{3} - \sqrt{2}$ ，则 $x^{2} y + x y^{2} =$ .

查看试题解析
13. 从甲、乙、丙三人中选一人参加环保知识决赛，经过两轮测试，他们的平均成绩都是88.9，方差分别是 $s_{甲}^{2} = 2.25$ ， $s_{乙}^{2} = 1.81$ ， $s_{丙}^{2} = 3.42$ ，你认为最适合参加决赛的选手是（填“甲”“乙”或“丙”）.

查看试题解析
14. 如图所示，直线a经过正方形ABCD的顶点A，分别过正方形的顶点B、D作BF⊥a于点F，DE⊥a于点E，若DE＝5，BF＝8则EF的长为.

查看试题解析
15. 如图，已知直线 $y = - \frac{4}{3} x + 8$ 与x轴、y轴分别交于点A和点B，M是OB上一点，若将 $△ A B M$ 沿AM翻折，点B恰好落在x轴上的点 $B'$ 处，则直线AM所对应的函数解析式是.

查看试题解析
16. 小明在某次投篮中刚好把球打到篮板的点D处后进球.已知小明与篮板底的距离 $B C = \sqrt{6}$ 米，眼睛与地面的距离 $A B = 1.7$ 米，眼睛与篮板的点D的距离 $A D = 2.5$ 米，则点D到地面的距离CD是米.

查看试题解析
17. 如图，在菱形 $A B C D$ 中，对角线 $A C ， B D$ 交于点 $O$ ，过点 $A$ 作 $A H ⊥ B C$ 于点 $H$ ，已知BO=4，S_菱形ABCD=24，则 $A H =$ ．

查看试题解析
18. 如图，点 $A_{0}$ 位于坐标原点，点 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， …， $A_{n}$ 在y轴的正半轴上，点 $B_{1}$ ， $B_{2}$ ， $B_{3}$ ， …， $B_{n}$ 在第一象限，点 $C_{1}$ ， $C_{2}$ ， $C_{3}$ ， …， $C_{n}$ 在第二象限，四边形 $A_{0} B_{1} A_{1} C_{1}$ 、四边形 $A_{1} B_{2} A_{2} C_{2}$ 、四边形 $A_{2} B_{3} A_{3} C_{3}$ ……四边形 $A_{n - 1} B_{n} A_{n} C_{n}$ 都是菱形， $∠ A_{0} B_{1} A_{1} = ∠ A_{1} B_{2} A_{2} = ∠ A_{2} B_{3} A_{3} = ⋯ = ∠ A_{n - 1} B_{n} A_{n} = 60 °$ .若 $A_{0} A_{1} ： A_{1} A_{2} ： A_{2} A_{3} ： ⋯ ： A_{n - 1} A_{n} = 1 ： 2 ： 4 ： ⋯ ： 2^{n - 1}$ ，且 $A_{0} A_{1} = 2$ ，则点 $B_{n}$ 的横坐标为.

查看试题解析

三、解答题（满分66分）

19. 先化简，再求值： $(\frac{5 x + 3 y}{x^{2} - y^{2}} + \frac{2 x}{y^{2} - x^{2}}) \div \frac{1}{x^{2} y - x y^{2}}$ ，其中 $x = \sqrt{5} + 1$ ， $y = \sqrt{5} - 1$ .

查看试题解析
20. 如图，在▱ABCD中，已知 $A D > A B$ .

(1)、作 $∠ B A D$ 的平分线交BC于点E，在AD上截取 $A F = A B$ ，连接EF；（要求：尺规作图，保留作图痕迹，不写作法.）

(2)、直接写出四边形ABEF的形状.

查看试题解析
21. 某校八年级甲、乙两班各有学生50人，为了解这两个班学生的身体素质情况，进行了抽样调查，过程如下，请补充完整.
⑴收集数据
从甲、乙两个班各随机抽取10名学生进行身体素质测试，测试成绩（百分制）如下：
甲班：65 75 75 80 60 50 75 90 85 65
乙班：90 55 80 70 55 70 95 80 65 70
⑵整理、描述数据
按如下分数段整理、描述这两组样本数据：

成绩x/分
          $50 \leq x < 60$
          $60 \leq x < 70$
          $70 \leq x < 80$
          $80 \leq x < 90$
          $90 \leq x < 100$
甲班
1
3
3
2
1
乙班
2
1
m
2
n
则 $m =$       ▲       ， $n =$       ▲      ；
⑶分析数据
①两组样本数据的平均数、中位数、众数如下表：

班级
平均数
中位数
众数
甲班
72
x
75
乙班
73
70
y
则 $x =$       ▲       ， $y =$       ▲      .
②若规定测试成绩在80分（含80分）以上的学生的身体素质为优秀，请估计乙班50名学生中身体素质为优秀的学生人数.

查看试题解析
22. 如图，正方形纸片ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G处，已知BE=1，求EF的长.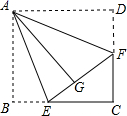

查看试题解析
23. 联想中垂线的性质，我们可引入如下概念：
定义：到三角形的两个顶点距离相等的点，叫做此三角形的“智慧心”.

(1)、举例：如图①，在 $△ A B C$ 中， $∠ P A B = ∠ P B A$ ，判断：点 $P$ （填“是”或“不是”） $△ A B C$ 的“智慧心”；

(2)、应用：如图②，若CD为等边三角形ABC的高，“智慧心”P在高CD上，且 $P D = \frac{1}{2} A B$ ，则 $∠ A P B$ 的度数为；

(3)、探究：已知 $△ A B C$ 为直角三角形， $∠ A = 90 °$ ， $∠ A B C = 60 °$ ， $A C = 4$ ， “智慧心”P在AC边上，则PA的长为.

查看试题解析
24. 某药店销售A，B两种型号的口罩，已知销售80只A型和45只B型的利润为21元；销售40只A型和60只B型的利润为18元.

(1)、求每只A型口罩和每只B型口罩的销售利润；

(2)、该药店计划一次购进两种型号的口罩共2000只，其中B型口罩的进货量不少于A型口罩的进货量且不超过它的3倍，设购进A型口罩x只，这2000只口罩的销售总利润为y元，求y关于x的函数关系式，并求出自变量x的取值范围；

(3)、在（2）的条件下，该药店购进A型、B型口罩各多少只，才能使销售总利润最大？

查看试题解析
25.

(1)、【感知】
如图①，四边形ABCD和四边形CEFG均为正方形.BE与DG的数量关系为；

(2)、【拓展】
如图②，四边形ABCD和四边形CEFG均为菱形，且 $∠ A = ∠ F$ .请判断BE与DG的数量关系，并说明理由；

(3)、【应用】
如图③，四边形ABCD和四边形CEFG均为菱形，点E在边AD上，点G在AD的延长线上.若 $A E = 2 E D$ ， $∠ A = ∠ F$ ， $△ E B C$ 的面积为9，求菱形CEFG的面积.

查看试题解析
26. 如图所示，在平面直角坐标系中，四边形ABCD是菱形，点A的坐标为 $(- 5 ， 4)$ ，点B，C在x轴上，点D在y轴上.

(1)、求点B的坐标；

(2)、动点P以每秒1个单位长度的速度从点O出发，沿射线OB方向运动，设点P运动的时间为t秒，连接PD，BD，设 $△ P B D$ 的面积为 $S (S \neq 0)$ ，求S与t的函数关系式（请直接写出自变量t的取值范围）；

(3)、在（2）的条件下，平面内是否存在点Q，使以A，C，P，Q为顶点的四边形为矩形？若存在，请直接写出点Q的坐标；若不存在，请说明理由.

查看试题解析

成绩x/分	$50 \leq x < 60$	$60 \leq x < 70$	$70 \leq x < 80$	$80 \leq x < 90$	$90 \leq x < 100$
甲班	1	3	3	2	1
乙班	2	1	m	2	n

班级	平均数	中位数	众数
甲班	72	x	75
乙班	73	70	y