黑龙江省齐齐哈尔市讷河市2022-2023学年七年级下册数学期末考试试卷

试卷更新日期：2023-07-14 类型：期末考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 下列各数是无理数的是（）

A、0 B、1 C、－1 D、 $\sqrt{2}$

查看试题解析
2. 下列说法不正确的是（）

A、0.09的平方根是±0.3 B、 $\sqrt{\frac{1}{9}} = \frac{1}{3}$ C、1的立方根是±1 D、0的立方根是0

查看试题解析
3. 如图，两条平行线 $a ， b$ 被直线 $c$ 所截，若 $∠ 1 = 5 0^{∘}$ ，则 $∠ 5$ 的度数为（）

A、 $5 0^{∘}$ B、 $13 0^{∘}$ C、 $12 0^{∘}$ D、 $15 0^{∘}$

查看试题解析
4. 估计 $\sqrt{14}$ 的值在（）

A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间

查看试题解析
5. 为了证明数轴上的点可以表示无理数，老师给学生设计了如下材料：如图，直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上一点由原点（记为点O）到达点A，点A对应的数是（）

A、 $π$ B、3.14 C、 $ - π$ D、－3.14

查看试题解析
6. 足球比赛中，每场比赛都要分出胜负，每队胜1场得3分，负一场扣1分，某队在8场比赛中得12分，若设该队胜的场数为 $x$ ，负的场数为 $y$ ，则可列方程组为（）

A、 ${\begin{array}{l} x + y = 8 \\ 3 x - y = 12 \end{array}$ B、 ${\begin{array}{l} x - y = 8 \\ 3 x - y = 12 \end{array}$ C、 ${\begin{array}{l} x + y = 8 \\ 3 x + y = 12 \end{array}$ D、 ${\begin{array}{l} x - y = 8 \\ 3 x + y = 12 \end{array}$

查看试题解析
7. 若 $x < y$ ，且 $(a - 3) x > (a - 3) y$ ，则a的取值范围是（）

A、 $a > 3$ B、 $a \leq 3$ C、 $a \geq 3$ D、 $a < 3$

查看试题解析
8. 已知点A坐标为4（5，4），将点A向下平移3个单位长度，再向左平移4个单位长度，得到A，则A点的坐标为（）

A、（2，0） B、（9，1） C、（1，1） D、（2，－1）

查看试题解析
9. 如图，把长方形 $A B C D$ 沿 $E F$ 折叠后，点D，C分别落在 $D^{'}$ ， $C^{'}$ 的位置．若 $∠ D^{'} E F = 65 °$ ，则 $∠ C^{'} F B$ 是（）

A、 $45 °$ B、 $50 °$ C、 $60 °$ D、 $65 °$

查看试题解析
10. 下列说法正确的有（）
①带根号的数都是无理数；
②立方根等于本身的数是0和1；
③－a一定没有平方根；
④实数与数轴上的点是一一对应的；
⑤两个无理数的差还是无理数

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每小题3分，共21分）

11. 16的算数平方根是．

查看试题解析
12. 如图，现要从村庄P修建一条连接公路AB的最短小路，过点P作 $P C ⊥ A B$ 于点C，沿PC修建公路就能满足小路最短，这样做的依据是．

查看试题解析
13. 已知一个有40个数据的样本，把它分成六组，第一组到第四组的频数分别为10，5，7，6，第五组的频率是0.10，则第六组的频率为．

查看试题解析
14. 已知点P（3，m）到x轴的距离为4，则点P的坐标为．

查看试题解析
15. 如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，AB＝6，DH＝2，平移距离为3，则阴影部分的面积为．

查看试题解析
16. 若不等式组 ${\begin{matrix} 2 x - 1 > 3 \\ x \leq a \end{matrix}$ 的整数解共有三个，则a的取值范围是．

查看试题解析
17. 如图，在平面直角坐标系中，一动点沿箭头所示的方向，每次移动一个单位长度，依次得到点 $P_{1} (0 ， 1)$ ， $P_{2} (1 ， 1)$ ， $P_{3} (1 ， 0)$ ， $P_{4} (1 ， - 1)$ ， $P_{5} (2 ， - 1)$ ， …，则 $P_{2023}$ 的坐标是．

查看试题解析

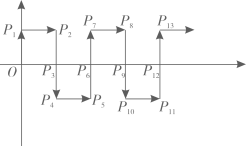
三、解答题（共69分）

18.

(1)、计算： $2 (\sqrt{3} - 1) - | \sqrt{3} - 2 | - \sqrt[3]{- 64}$ ．

(2)、解方程组： ${\begin{array}{l} x - 2 = 2 (y - 1) ， \\ 2 (x - 2) + (y - 1) = 5 ； \end{array}$

查看试题解析
19. 解不等式组： ${\begin{array}{l} 2 x + 3 > \frac{3 + x}{2} \\ 2 x - 6 \leq 6 - 2 x \end{array}$ ；并写出它的整数解．

查看试题解析
20. 如图是由边长为1的小正方形组成的网格，每个小正方形的顶点叫做格点，点A，B，C均在格点上．若点A，B的坐标分别为A（1，1），B（4，0），请解答下列问题：

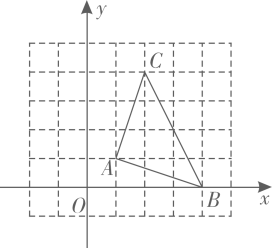(1)、直接写出点C的坐标；

(2)、将△ABC先向左平移2个单位长度，再向下平移1个单位长度得到△DEF，（点A，B，C的对应点分别为D，E，F），画出△DEF，并直接写出点F的坐标；

(3)、直接写出（2）中四边形DBCF的面积为．

查看试题解析
21. 家庭过期药品属于“国家危险废物”，处理不当将污染环境，危害健康。某市药监部门为了了解市民家庭处理过期药品的方式，决定对全市家庭作一次简单随机抽样调查：

(1)、下列选取样本的方法最合理的一种是（只需填上正确答案的序号）
①在市中心某个居民区以家庭为单位随机抽取
②在全市医务工作者中以家庭为单位随机抽取
③在全市常住人口中以家庭为单位随机抽取

(2)、本次抽样调查发现，接受调查的家庭都有过期药品，现将有关数据呈现如下图：
①m= ▲ ， n= ▲ ；
②补全条形统计图；
③根据调查数据，你认为该市市民家庭处理过期药品最常见的方式是什么？
④家庭过期药品的正确处理方式是送回收点，若该市有180万户家庭，请估计大约有多少户家庭处理过期药品的方式是送回收点．

查看试题解析
22. 已知：如图，AD⊥BC，EF⊥BC ，∠1=∠2.求证：DG∥AB.

查看试题解析
23. 为更好地落实“双减”要求，提高课后延时服务质量，某校根据学校实际，决定增设更多运动课程，让更多学生参加体育锻炼，各班自主选择购买两种体育器材．

(1)、七年一班准备统一购买新的足球和跳绳。请你根据上图中班长和售货员的对话信息，分别求出每个足球和每根跳绳的售价；

(2)、由于运动课程得到同学们的喜欢，足球和跳绳需求量增大，学校计划再次购买足球和跳绳一共10个，合计费用不超过650元，其中足球至少购买3个，则有哪几种购买方案？并求出每种方案所花的费用．

查看试题解析
24. 在平面直角坐标系中，已知点A（a，0），B（b，3），C（4，0），且满足 $| a + b | + {(a - b + 6)}^{2} = 0$ ，线段AB交y轴于点F，点D是y轴正半轴上的一点．

(1)、求出点A，B的坐标；

(2)、如图2，若 $D B ∥ A C$ ， $∠ B A C = α$ ，且AM，DM分别平分 $∠ C A B$ ， $∠ O D B$ ，求 $∠ A M D$ 的度数；（用含a的代数式表示）

(3)、如图3，三角形ABC向右平移，使点A与原点O重合，此时坐标轴上是否存在一点P（不与点C重合），使得△ABP的面积和△ABC的面积相等？若存在，请直接写出P点坐标；若不存在，请说明理由．

查看试题解析