（人教版）2023-2024学年九年级数学上册21.1一元二次方程同步分层训练（培优卷）

试卷更新日期：2023-07-13 类型：同步测试

进入出卷网下载

一、选择题

1. 设a，b是方程 $x^{2} + x - 2023 ＝ 0$ 的两个实数根，则 $a^{2} + 2 a + b$ 的值为（）

A、2024 B、2021 C、2023 D、2022

查看试题解析
2. 已知 $\frac{a^{2} - c}{a} - 1 = 0$ ， $\frac{b^{2} - c}{b} - 1 = 0$ ，若 $a \neq b$ ，则下列等式成立的是（）

A、 $a + b = - 1$ B、 $a + b = 1$ C、 $a - b = 1$ D、 $a - b = - 1$

查看试题解析
3. 如图1，矩形ABCD中，点E为BC的中点，点P沿BC从点B运动到点C，设B，P两点间的距离为x，PA﹣PE＝y，图2是点P运动时y随x变化的关系图象，则BC的长为（）

A、4 B、5 C、6 D、7

查看试题解析
4. 下列说法：
$①$ 若一元二次方程 $x^{2} + b x + a = 0$ 有一个根是 $- a (a \neq 0)$ ，则代数式 $a - b$ 的值是 $- 1$ $②$ 若 $a + b + c = 0$ ，则 $x = a + b + c$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的一个根 $③$ 若 $b = 2 a + 3 c$ ，则一元二次方程 $a x^{2} + b x + c = 0$ 有不相等的两个实数根 $④$ 当m取整数 $- 1$ 或1时，关于x的一元二次方程 $m x^{2} - 4 x + 4 = 0$ 与 $x^{2} - 4 m x + 4 m^{2} - 4 m - 5 = 0$ 的解都是整数.其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 欧几里得的《原本）记载，形如x²+ax=b²的方程的图解法是：画Rt△ABC，∠ACB=90°，BC= $\frac{a}{2}$ ，AC=b，再在斜边AB上截取BD= $\frac{a}{2}$ ，则该方程的一个正根是（）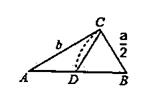

A、AC的长 B、AD的长 C、BC的长 D、CD的长

查看试题解析
6. 如图，某校劳动实践课程试验园地是长为 $20 m$ ，宽为 $18 m$ 的矩形，为方便活动，需要在园地中间开辟一横两纵共三条等宽的小道．如果园地余下的面积为 $306 m^{2}$ ，则小道的宽为多少？设小道的宽为 $x m$ ，根据题意，可列方程为（）

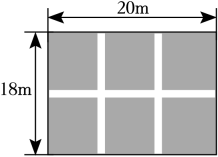A、 $(20 - 2 x) (18 - x) = 306$ B、 $(20 - x) (18 - 2 x) = 306$ C、 $20 \times 18 - 2 \times 18 x - 20 x + x^{2} = 306$ D、 $20 \times 18 - 2 \times 20 x - 18 x + x^{2} = 306$

查看试题解析
7. 如图，某校生物兴趣小组用长为18米的篱笆，一面利用墙（墙的最大可用长度为11米），围成中间隔有一道篱笆的长方形花圃 $A B C D$ ，为了方便出入，建造篱笆花圃时在 $B C$ 边留了宽为1米的两个进出口（不需材料），若花圃的面积刚好为40平方米，设 $A B$ 的长为x米，则可列方程为（）

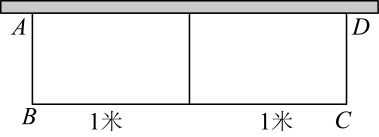A、 $x (18 - 3 x) = 40$ B、 $x (20 - 2 x) = 40$ C、 $x (22 - 3 x) = 40$ D、 $x (20 - 3 x) = 40$

查看试题解析
8. 关于x的一元二次方程 $a x^{2} + b x = c (a c \neq 0)$ 一个实数根为2022，则方程 $c x^{2} + b x = a$ 一定有实数根（）

A、2022 B、 $\frac{1}{2022}$ C、−2022 D、− $\frac{1}{2022}$

查看试题解析
9. 已知关于x的一元二次方程 $m {(x - h)}^{2} - k = 0$ （m，h，k均为常数且 $m \neq 0$ ）的解是 $x_{1} = 2$ ， $x_{2} = 5$ ，则关于x的一元二次方程 $m {(x - h + 1)}^{2} = k$ 的解是（）

A、 $x_{1} = - 2$ ， $x_{2} = - 5$ B、 $x_{1} = - 4$ ， $x_{2} = - 1$ C、 $x_{1} = 1$ ， $x_{2} = 4$ D、 $x_{1} = - 3$ ， $x_{2} = - 6$

查看试题解析
10. 如果关于x的一元二次方程 $a x^{2} + b x + 1 = 0$ 的一个解是x＝1，则代数式2022－a－b的值为（）

A、－2022 B、2021 C、2022 D、2023

查看试题解析

二、填空题

11. 等腰三角形的三边的长是a 、b、4，其中a、b是方程x²-6x+c=0两个根，则此三角形的三边长是．

查看试题解析
12. 若边长为5的菱形的两条对角线的长分别是关于x的一元二次方程 $x^{2} + (2 m + 1) x + m^{2} - 4 = 0$ 两根的2倍，则m的值为．

查看试题解析
13. 已知关于x的一元二次方程 $x^{2} + (2 k + 1) x + k^{2} - 2 = 0$ 的两根x₁和x₂ ，且 $(x_{1} - 2) (x_{1} - x_{2}) = 0$ ，则k的值是.

查看试题解析
14. 若关于x的三个方程x²+4mx+4m²+2m+3=0，x²+（2m+1）x+m²=0，（m﹣1）x²+2mx+m﹣1=0中至少有一个方程有实根，则m的取值范围是．

查看试题解析
15. 关于x的方程（1-m²）x²+2mx-1=0的所有根都是比1小的正实数，则实数m的取值范围是．

查看试题解析

三、解答题

16. 已知关于x的一元二次方程（a+1）x²+2x+1﹣a²＝0有一个根为﹣1，求a的值．

查看试题解析
17. 关于x的方程 $x^{2} - 2 x + 2 m - 1 = 0$ 有实数根，且m为正整数，求m的值及此时方程的根．

查看试题解析
18. 已知m是方程x²﹣x-2=0的一个根，求代数式 $(m^{2} - m)(m - \frac{2}{m} + 1)$ 的值.

查看试题解析
19. 已知关于x的一元二次方程（m﹣3）x²﹣6x+m²﹣9＝0的常数项为0，求m的值及此方程的解.

查看试题解析

四、综合题

20. 如图，在△ABD中，AB=AD，AO平分∠BAD，过点D作AB的平行线交AO的延长线于点C，连接BC

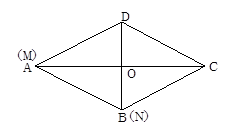(1)、求证：四边形ABCD是菱形．

(2)、如果OA，OB(OA>OB)的长（单位：米）是一元二次方程 $x^{2} - 7 x + 12 = 0$ 的两根，求AB的长以及菱形ABCD的面积．

(3)、若动点M从A出发，沿AC以2m/S的速度匀速直线运动到点C，动点N从B 出发，沿BD以1m/S的速度匀速直线运动到点D，当M运动到C点时运动停止．若M、N同时出发，问出发几秒钟后，△MON的面积为 $\frac{1}{4} m^{2}$ ？

查看试题解析
21. 已知m ， n分别是关于x的一元二次方程ax²+bx+c＝a与ax²+bx+c＝b的一个根，且m＝n+1．

(1)、当m＝2，a＝﹣1时，求b与c的值；

(2)、用只含字母a ， n的代数式表示b；

(3)、当a＜0时，函数y＝ax²+bx+c满足b²﹣4ac＝a ， b+c≥2a ， n≤﹣ $\frac{1}{2}$ ，求a的取值范围．

查看试题解析
22. 小明解关于 $x$ 的一元二次方程 $x^{2} + b x + 5 = 0$ 时，在解答过程中写错了常数项，因而得到方程的两个根是4和2．

(1)、求 $b$ 的值；

(2)、若菱形的对角线长是关于 $x$ 的一元二次方程 $x^{2} + b x + 5 = 0$ 的解，求菱形的面积．

查看试题解析
23.

(1)、已知m是方程x²-x-1=0的一个根，求m（m+1）²-m²（m+3）+4的值；

(2)、一次函数y=2x+2与反比例函数y= $\frac{k}{x}$ （k≠0）的图象都经过点A（1，m），y=2x+2的图象与x轴交于点B。

①求点B的坐标及反比例函数的表达式；

②点C（0，-2），若四边形ABCD是平行四边形，请在直角坐标系内画出 $▱$ ABCD，直接写出点D的坐标，并判断D点是否在此反比例函数的图象上，并说明理由。

查看试题解析
24. 在平面直角坐标系中，矩形 $O A B C$ 的边 $O A$ 、 $O C$ 分别在x轴的正半轴、y轴的正半轴上，且 $O A$ 、 $O C$ 的长是方程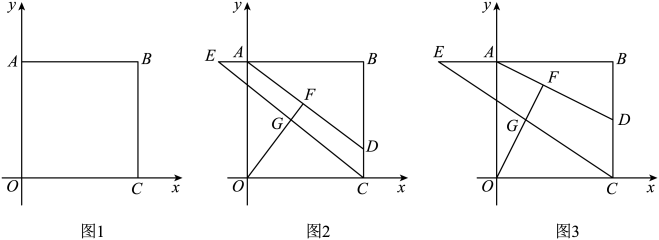 $x^{2} - 20 x + 100 = 0$ 的两个根．

(1)、如图1，求点C坐标；

(2)、如图2，点D在 $C B$ 上，点E在 $B A$ 的延长线上，且 $C D = A E$ ．连接 $A D 、 C E$ ，过点O作 $O F ⊥ A D$ 交 $C E$ 于点G，垂足为点F．设 $C D$ 长为m，点G的横坐标为n，求n与m的函数关系式（不要求写出自变量m的取值范围）；

(3)、如图3，在（2）的条件下，当 $F G ： G O = 3 ： 5$ 时，求直线 $A D$ 的解析式．

查看试题解析

（人教版）2023-2024学年九年级数学上册21.1一元二次方程 同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年九年级数学上册21.1一元二次方程同步分层训练（培优卷）