（人教版）2023-2024学年八年级数学上册12.3角的平分线的性质 同步分层训练（培优卷）
试卷更新日期：2023-07-13 类型：同步测试
一、选择题
-
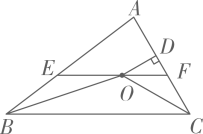
1. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EFBC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：①∠BOC＝90°∠A，②∠EBO∠AEF，③∠DOC+∠OCB＝90°，④设OD＝m，AE+AF＝n，则S△AEF ． 其中正确的结论有（ ）
A、1个 B、2个 C、3个 D、4个2. 如图， ， 平分交于点 ， ， ， ， 分别是 ， 延长线上的点，和的平分线交于点下列结论：；；平分；为定值其中结论正确的有（ ）
A、1个 B、2个 C、3个 D、4个3. 如图，在△ABC中，若分别以AB、AC为边作△ABD和△ACE，且∠DAB＝∠CAE＝α，AD＝AB，AC＝AE，DC、BE交于点P，连接AP，则∠APC的度数为（ ）
A、90°﹣α B、90°+α C、90°﹣α D、90°+α4. 如图，点E是的中点， ， ， 平分 ， 下列结论：①；②；③；④.其中正确的是（ ）
A、①②④ B、①②③④ C、②③④ D、①③5. 如图， 的外角 ， 的平分线 ， 相交于点P， 于E， 于F，下列结论：（1） ；（2）点P在 的平分线上；（3） ；（4）若 ，则 ，其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个6. 如图，△ABC中，∠ABC、∠EAC的角平分线BP、AP交于点P，延长BA、BC，PM⊥BE，PN⊥BF，则下列结论中正确的个数（ ）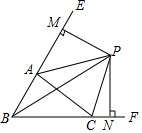
①CP平分∠ACF；②∠ABC+2∠APC=180°；③∠ACB=2∠APB；④S△PAC=S△MAP+S△NCP.
A、1个 B、2个 C、3个 D、4个7. 如图 是 的角平分线， 于E，点F，G分别是 ， 上的点，且 ， 与 的面积分别是10和3，则 的面积是（ ）
A、4 B、5 C、6 D、78. 如图，在△ABC中，∠BAC和∠ABC的平分线AE，BF相交于点O，AE交BC于E，BF交AC于F，过点O作OD⊥BC于D，下列四个结论：①∠AOB＝90°+ ∠C；②当∠C＝60°时，AF+BE＝AB； ③若OD＝a，AB+BC+CA＝2b，则S△ABC＝ab.其中正确的是（ ）
A、①② B、②③ C、①②③ D、①③9. 如图，在△OAB和△OCD中，OA＝OB，OC＝OD，OA＞OC，∠AOB＝∠COD＝30°，连接AC，BD交于点M，AC与OD相交于E，BD与OA相交于F，连接OM.则下列结论中：①AC＝BD；②∠AMB＝30°；③△OEM≌△OFM；④MO平分∠BMC.正确的个数有（ ）
A、4个 B、3个 C、2个 D、1个10. 如图，点P为定角∠AOB平分线上的一个定点，且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：①PM=PN；②OM+ON的值不变；③MN的长不变；④四边形PMON的面积不变，其中，正确结论的是（ ）
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
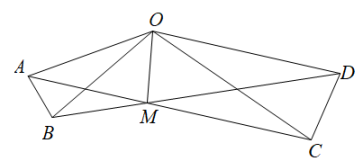
11. 如图，在△AOB和△COD中，OA＝OB ， OC＝OD（OA＜OC），∠AOB＝∠COD＝α ， 直线AC ， BD交于点M ， 连接OM ． 以下结论：①AC＝BD；②∠OAM＝∠OBM；③∠AMB＝α；④OM平分∠BOC ． 其中正确的是 ． （填序号）
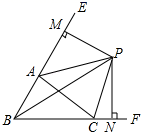
12. 如图， ABC中，∠ABC、∠EAC的角平分线BP、AP交于点P，延长BA、BC，PM⊥BE，PN⊥BF，则下列结论中正确的是.①CP平分∠ACF；②∠ABC＋2∠APC＝180°；③∠ACB＝2∠APB；④S△PAC＝S△MAP＋S△NCP.
13. 如图，AP，BP分别平分△ABC内角∠CAB和外角∠CBD，连接CP，若∠ACP＝130°，则∠APB＝ ．
14. 如图，R△ABC中，∠C=90°，∠BAC的角平分线AE与AC的中线BD交于点F，P为CE中点，连结PF，若CP=2，S△BFP=15，则AB的长度为。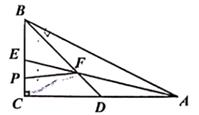
15. 在数学活动课上，小明提出这样一个问题：∠B＝∠C＝90°，E是BC的中点，DE平分∠ADC ， ∠CDE＝55°．如图，则∠EAB的度数为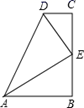
三、解答题
-
16. 如图，四边形ABCD中AD=AB，∠DAB+∠BCD=180°，求证：CA平分∠DCB
17. 如图，在 中， 和 的平分线交于点 ，过点 作 ，交 于 ，交 于 ，若 ， ，试求 的值．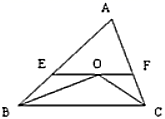
18. 如图（a），∠DAB+∠ABC+∠BCE=360°
(1)、求证：AD∥CE(2)、如图（b），AG、CG分别平分∠BAD、∠BCE，BF∥AG交GC的延长线于F，判断∠ABC与∠F的数量关系，并证明；(3)、如图（c），AN平分∠HAB，BP平分∠ABC，BQ∥AN，CM平分∠BCT交BQ的反向延长线于M，① 的值不变，② 的值不变；其中只有一个结论正确，请择一证明．19. 已知：△ABC中，记∠BAC=α，∠ACB=β．
(1)、如图1，若AP平分∠BAC，BP，CP分别平分△ABC的外角∠CBM和∠BCN，BD⊥AP于点D，用α的代数式表示∠BPC的度数，用β的代数式表示∠PBD的度数.
(2)、如图2，若点P为△ABC的三条内角平分线的交点，BD⊥AP于点D，猜想（1）中的两个结论是否发生变化，补全图形并直接写出你的结论．四、综合题
-
20. 综合与实践：
问题情境：已知是的平分线，P是射线上的一点，点C，D分别在射线 ， 上，连接 ．
(1)、初步探究：如图1，当 ， 时，与的数量关系是；(2)、深入探究：如图2，点C，D分别在射线 ， 上运动，且 ， 当时，与在（1）中的数量关系还成立吗？请说明理由；(3)、拓展应用：如图3，如果点C在射线上运动，且 ， 当时，点D落在了射线的反向延长线上，若点P到的距离为3， ， 求的长（直接写出答案）．21. 【概念认识】如图①，在∠ABC中，若∠ABD＝∠DBE＝∠EBC，则BD，BE叫做∠ABC的“三分线”．其中，BD是“邻AB三分线”，BE是“邻BC三分线”．
(1)、【问题解决】
如图②，在△ABC中，∠A＝80°，∠B＝45°，若∠B的三分线BD交AC于点D，求∠BDC的度数；(2)、如图③，在△ABC中，BP、CP分别是∠ABC邻BC三分线和∠ACB邻BC三分线，且∠BPC＝140°，求∠A的度数；(3)、【延伸推广】
在△ABC中，∠ACD是△ABC的外角，∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P．若∠A＝m°（m＞54），∠B＝54°，直接写出∠BPC的度数．（用含m的代数式表示）
