(人教版)2023-2024学年八年级数学上册12.3角的平分线的性质 同步分层训练(提升卷)
试卷更新日期:2023-07-13 类型:同步测试
一、选择题
-
1. 下列四个命题:①直线外一点到这条直线的垂线段叫做点到直线的距离;②角平分线上的点到角两边的距离相等;③过一点有且只有一条直线与这条直线平行;④如果一个角的两边分别垂直于另一个角的两边,那么这两个角相等.其中真命题的个数是( )A、0个 B、1个 C、2个 D、4个2. 如图,在中, , 以顶点为圆心,适当长为半径画弧,分别交边、于点、 , 再分别以点、为圆心,大于的长为半径画弧,两弧交于点 , 作射线交边于点 , 若 , , 则的面积是( )
 A、15 B、30 C、45 D、603. 如图,是中的平分线,交于点 , 交于点 , 若 , , , 则的长为( )
A、15 B、30 C、45 D、603. 如图,是中的平分线,交于点 , 交于点 , 若 , , , 则的长为( ) A、 B、4 C、5 D、64. 如图,在中, , 以点A为圆心,适当长为半径画弧,分别交、于点D,E,再分别以点D、E为圆心,大于为半径画弧,两弧交于点F,作射线交边于点G,若 , , 则的面积是( )
A、 B、4 C、5 D、64. 如图,在中, , 以点A为圆心,适当长为半径画弧,分别交、于点D,E,再分别以点D、E为圆心,大于为半径画弧,两弧交于点F,作射线交边于点G,若 , , 则的面积是( ) A、2 B、3 C、4 D、55. 如图,在四边形中, , 平分 , , 则的面积是( )
A、2 B、3 C、4 D、55. 如图,在四边形中, , 平分 , , 则的面积是( ) A、6 B、8 C、10 D、126. 如图.点P是的角平分线上的一点,于点E,已知 , 则点P到的距离是( )
A、6 B、8 C、10 D、126. 如图.点P是的角平分线上的一点,于点E,已知 , 则点P到的距离是( ) A、18 B、12 C、6 D、97. 如图,中, , 平分交于点P,若 , , 则的面积是( )
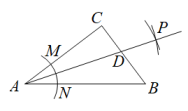
A、18 B、12 C、6 D、97. 如图,中, , 平分交于点P,若 , , 则的面积是( ) A、 B、 C、 D、8. 如图,点是的外角平分线上一点,且满足 , 过点D作于点E,交的延长线于点F,则下列结论中,其中正确的结论有( )①;②平分;③;④.
A、 B、 C、 D、8. 如图,点是的外角平分线上一点,且满足 , 过点D作于点E,交的延长线于点F,则下列结论中,其中正确的结论有( )①;②平分;③;④. A、1个 B、2个 C、3个 D、4个9. 如图,在四边形中, , , 连接 , , 垂足为C,并且 , 点E是边上一动点,则的最小值是( )
A、1个 B、2个 C、3个 D、4个9. 如图,在四边形中, , , 连接 , , 垂足为C,并且 , 点E是边上一动点,则的最小值是( ) A、1.5 B、3 C、3.5 D、410. 如图,中, , 平分 , , , 则的面积为( )
A、1.5 B、3 C、3.5 D、410. 如图,中, , 平分 , , , 则的面积为( )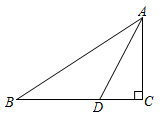 A、20 B、10 C、15 D、30
A、20 B、10 C、15 D、30二、填空题
-
11. 如图,在中,是边上的高,平分 , 交于点E, , 若的面积为9,则的长为.
 12. 如图,在四边形中, , , , , 则点到边的距离等于 .
12. 如图,在四边形中, , , , , 则点到边的距离等于 . 13. 如图,在中, , 是的角平分线,如果 , , 那么 .
13. 如图,在中, , 是的角平分线,如果 , , 那么 . 14. 如图,是的角平分线,于 , 的面积为 , , 则.
14. 如图,是的角平分线,于 , 的面积为 , , 则. 15. 如图所示,点O是内一点,平分 , 于点D,连接 , 若 , 则的面积是 .
15. 如图所示,点O是内一点,平分 , 于点D,连接 , 若 , 则的面积是 .
三、解答题
-
16. 如图,AD=BD,∠CAD+∠CBD=180°,求证:CD平分∠ACB.
 17. 如图, , M是的中点,平分 , 且 , 求的度数
17. 如图, , M是的中点,平分 , 且 , 求的度数 18. 如图,∠ACB=90°,BD平分∠ABC交AC于D,DE⊥AB于E,ED的延长线交BC的延长线于F. 求证:AE=CF.
18. 如图,∠ACB=90°,BD平分∠ABC交AC于D,DE⊥AB于E,ED的延长线交BC的延长线于F. 求证:AE=CF. 19. 如图:在 , , 于 , 于 , 、相交于求证:平分 .
19. 如图:在 , , 于 , 于 , 、相交于求证:平分 .
四、综合题
-
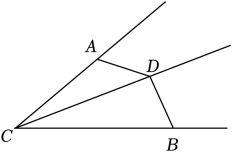
20. 如图,在中,的平分线交于点 , 过点作交于点 , 过点作交于点.
 (1)、求证:是的平分线;(2)、若 , 若 , 求的度数.
(1)、求证:是的平分线;(2)、若 , 若 , 求的度数.