(人教版)2023-2024学年八年级数学上册12.3角的平分线的性质 同步分层训练(基础卷)
试卷更新日期:2023-07-13 类型:同步测试
一、选择题
-
1. 如图, , 以点为圆心,小于的长为半径作圆弧,分别交 , 于 , 两点,再分别以 , 为圆心,以大于长为半径作圆弧两条弧交于点 , 作射线交于点 , 若 , 则( )
 A、 B、 C、 D、2. 如图,的三边AB,BC,CA长分别是20,30,40,其三条角平分线将分为三个三角形,则等于( ).
A、 B、 C、 D、2. 如图,的三边AB,BC,CA长分别是20,30,40,其三条角平分线将分为三个三角形,则等于( ). A、1∶1∶1 B、1∶2∶3 C、2∶3∶4 D、3∶4∶53. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D.已知AB=16,CD=5,则△ABD的面积为( )
A、1∶1∶1 B、1∶2∶3 C、2∶3∶4 D、3∶4∶53. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D.已知AB=16,CD=5,则△ABD的面积为( )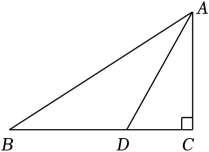 A、80 B、40 C、20 D、104. 如图,平分 , 于点 , 若 , 点是边上一动点,关于线段叙述正确的是( )
A、80 B、40 C、20 D、104. 如图,平分 , 于点 , 若 , 点是边上一动点,关于线段叙述正确的是( ) A、 B、 C、 D、5. 如图,OP平分∠AOB,点E为OA上一点,OE=4,点P到OB的距离是2,则△POE的面积为( )
A、 B、 C、 D、5. 如图,OP平分∠AOB,点E为OA上一点,OE=4,点P到OB的距离是2,则△POE的面积为( ) A、4 B、5 C、6 D、76. 如图,△ABC中, ,∠CAB的角平分线AD交BC于D, 于E, ,且 ,则BC的长是( )
A、4 B、5 C、6 D、76. 如图,△ABC中, ,∠CAB的角平分线AD交BC于D, 于E, ,且 ,则BC的长是( ) A、6cm B、4cm C、10cm D、以上都不对7. 已知:在 中, , 平分 交BC于D,若 ,且 ,则点D到AB边的距离为( )A、18 B、12 C、14 D、168. 如图①,已知∠AOB,用直尺和圆规作∠AOB的平分线.
A、6cm B、4cm C、10cm D、以上都不对7. 已知:在 中, , 平分 交BC于D,若 ,且 ,则点D到AB边的距离为( )A、18 B、12 C、14 D、168. 如图①,已知∠AOB,用直尺和圆规作∠AOB的平分线.如图②,步骤如下:
第一步,以点O为圆心,适当长为半径画弧,交OA于M,交OB于点N.
第二步,分别以点M,N为圆心,以a为半径画弧,两弧在∠AOB的内部相交于点C.
第三步,画射线OC.射线OC即为所求.
下列说法正确的是( )
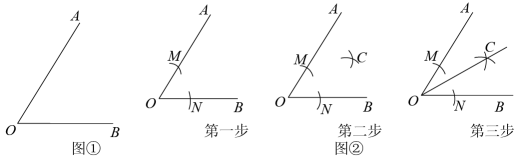 A、a>0 B、 C、 D、9. 如图,在Rt△ABC中,∠C=90°,AD是∠BAC平分线,DE⊥AB,垂足为E,若CD=10,则DE的长度为( )
A、a>0 B、 C、 D、9. 如图,在Rt△ABC中,∠C=90°,AD是∠BAC平分线,DE⊥AB,垂足为E,若CD=10,则DE的长度为( ) A、 B、 C、 D、10. 在中, , 的角平分线交于点 , 则点到的距离是( )
A、 B、 C、 D、10. 在中, , 的角平分线交于点 , 则点到的距离是( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
11. 如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E.若S△ABC=7,DE=2,AB=4,则AC的长是
 12. 如图,在△ABC中,∠C=90°,BD平分∠ABC,DC=5,则点D到AB的距离为 .
12. 如图,在△ABC中,∠C=90°,BD平分∠ABC,DC=5,则点D到AB的距离为 .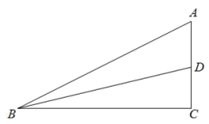 13. 如图,在中,平分交于点 , , 垂足为若 , , 则的面积为.
13. 如图,在中,平分交于点 , , 垂足为若 , , 则的面积为. 14. 如图,在△ABC中,∠C=90°,AD平分∠CAB,BD=4,点D到AB的距离为2,则BC= .
14. 如图,在△ABC中,∠C=90°,AD平分∠CAB,BD=4,点D到AB的距离为2,则BC= . 15. 如图,BD平分∠ABC,DE⊥AB于点E,DF⊥BC于点F,AB=7,BC=8.若 , 则DE= .
15. 如图,BD平分∠ABC,DE⊥AB于点E,DF⊥BC于点F,AB=7,BC=8.若 , 则DE= .
三、解答题
-
16. 如图,在中,是的中点, , , 垂足分别是点、 , . 求证:平分 .
 17. 已知,如图AC平分∠BAD,CE⊥AB于E点,CF⊥AD于F点,且BC=DC.求证:BE=DF.
17. 已知,如图AC平分∠BAD,CE⊥AB于E点,CF⊥AD于F点,且BC=DC.求证:BE=DF. 18. 如图, 是 的平分线,点 是线段 上的一点, , .
18. 如图, 是 的平分线,点 是线段 上的一点, , .
求证: .
19. 如图,在 中, 是高, 是角平分线, , 交于点F, = 0°, =70°,求 的度数
四、综合题
-
20. 如图,在Rt△ABC中,∠C=90°.
 (1)、作∠BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法).(2)、在(1)的条件下,若∠BAC=28°,求∠ADB的度数.
(1)、作∠BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法).(2)、在(1)的条件下,若∠BAC=28°,求∠ADB的度数.


