（人教版）2023-2024学年八年级数学上册12.2三角形全等的判定同步分层训练（培优卷）

试卷更新日期：2023-07-13 类型：同步测试

进入出卷网下载

一、选择题

1. 如图， $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ 、 $B M$ 是 $A C$ 边的中线，有 $A D ⊥ B M$ ；垂足为点 $E$ 交 $B C$ 于点 $D$ ．且 $A H$ 平分 $∠ B A C$ 交 $B M$ 于 $N$ ．交 $B C$ 于 $H$ ．连接 $D M$ ．则下列结论：
① $∠ A M B = ∠ C M D$ ；② $H N = H D$ ；③ $B N = A D$ ；④ $∠ B N H = ∠ M D C$ ；

错误的有（）个．

A、0 B、1 C、3 D、4

查看试题解析
2. 如图，在 $△ A O B$ 和 $△ C O D$ 中， $O A = O B ， O C = O D ， O A < O C ， ∠ A O B = ∠ C O D = 36 °$ ．连接AC，BD交于点M，连接OM．则下列结论：① $∠ A M B = 36 °$ ；② $A C = B D$ ；③ $O M$ 平分 $∠ A O D$ ；④ $M O$ 平分 $∠ A M D$ ．其中正确结论的个数为（　　）

A、4 B、3 C、2 D、1

查看试题解析
3. 如图，在四边形ABCD中，AD∥BC，若∠DAB的角平分线AE交CD于E，连结BE，且BE平分∠ABC，则以下命题不正确的是（）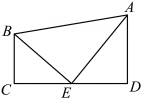

A、BC+AD＝CD B、E为CD中点 C、∠AEB＝90° D、S_△_ABE＝ $\frac{1}{2}$ S_四边形_ABCD

查看试题解析
4. 如图， $△ ABC$ 中， $∠ BAC = 60 °$ ， $∠ ABC < 60 °$ ，三条角平分线 $AD$ 、 $BE$ 、 $CF$ 交于 $O$ ， $OH ⊥ BC$ 于 $H .$ 下列结论： $① ∠ BOC = 120 °$ ； $② ∠ DOH = ∠ OCB - ∠ OBC$ ； $③ OD$ 平分 $∠ BOC$ ； $④ BF + CE = BC .$ 其中正确的结论个数有（）

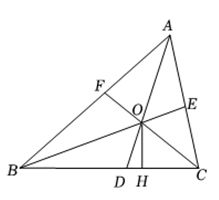A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，在 $△ A B C$ 中 $A B = A C$ ， $∠ B = ∠ A C D = 45 °$ ，D，E是BC上两点，且 $∠ D A E = 45 °$ ，过点A作 $A F ⊥ A D$ ，垂足是A，过点C作 $C F ⊥ B C$ ，垂足是C，CF交AF于点F，连接EF.给出下列结论：① $△ A B D ≌ △ A C F$ ；② $D E = E F$ ；③若 $S_{△ A D E} = 10$ ， $S_{△ C E F} = 4$ ，则 $S_{△ A B C} = 24$ ；④ $B D + C E = D E$ .其中正确结论的字号是（）

A、①②③ B、②③④ C、①③④ D、①②④

查看试题解析
6. 如图，在 $3 \times 3$ 的网格中，每一个小正方形的边长都是1，点 $A$ ， $B$ ， $C$ ， $D$ 都在格点上，连接 $A C$ ， $B D$ 相交于 $P$ ，那么 $∠ A P B$ 的大小是（）

A、 $80 °$ B、 $60 °$ C、 $45 °$ D、 $30 °$

查看试题解析
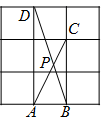7. 如图，Rt△ACB中，∠ACB=90°，△ACB的角平分线AD，BE相交于点P，过P作PF⊥AD交BC的延长线于点F，交AC于点H，则下列结论：①∠APB=135°；②AD=PF+PH；③DH平分∠CDE；④S_{四边形ABDE}= $\frac{7}{4}$ S_△ABP；⑤S_△APH=S_△ADE ，其中正确的结论有（）个

A、2 B、3 C、4 D、5

查看试题解析
8. 如图，在 $△ A B C$ 中， $A D$ 是 $B C$ 边上的高， $∠ B A F = ∠ C A G = 90 °$ ， $A B = A F$ ， $A C = A G$ .连接 $F G$ ，交 $D A$ 的延长线于点E，连接 $B G$ ， $C F$ .则下列结论：① $B G = C F$ ；② $B G ⊥ C F$ ；③ $B C = 2 A E$ ；④ $E F = E G$ ，其中正确的有（）

A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析
9. 如图，在 $△ A B C$ 中，已知 $A D ⊥ B C$ 于点 $D$ ， $A E$ 平分 $∠ C A D$ ，交 $B C$ 于点 $E$ ，过点 $E$ 作 $E F // A C$ ，分别交 $A B$ 、 $A D$ 于点 $F$ 、 $G$ ， $G D = G F$ .则下列结论：① $∠ C = ∠ B A D$ ；② $∠ B A C = 90 °$ ；③点 $E$ 是 $B C$ 的中点；④ $∠ B = 2 ∠ A E F$ ；⑤ $△ A B E$ 为等边三角形.其中结论正确的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
10. 程老师制作了如图1所示的学具，用来探究“边边角条件是否可确定三角形的形状”问题，操作学具时，点Q在轨道槽AM上运动，点P既能在以A为圆心、以8为半径的半圆轨道槽上运动，也能在轨道槽QN上运动，图2是操作学具时，所对应某个位置的图形的示意图．

有以下结论：

①当∠PAQ=30°，PQ=6时，可得到形状唯一确定的△PAQ

②当∠PAQ=30°，PQ=9时，可得到形状唯一确定的△PAQ

③当∠PAQ=90°，PQ=10时，可得到形状唯一确定的△PAQ

④当∠PAQ=150°，PQ=12时，可得到形状唯一确定的△PAQ

其中所有正确结论的序号是（）

A、②③ B、③④ C、②③④ D、①②③④

查看试题解析

二、填空题

11. 如图，点F坐标为 $(- 4 ， - 4)$ ，点 $G (0 ， m)$ 在y轴负半轴，点 $H (n ， 0)$ 在 $x$ 且轴的正半轴，且 $F H ⊥ F G$ ， $F H = F G$ ，则 $m + n$ 的值为．

查看试题解析
12. 如图是5×5的正方形网格，△ABC的顶点都在小正方形的顶点上，像△ABC这样的三角形叫格点三角形，画与△ABC有一条公共边且全等的格点三角形，这样的格点三角形最多可以画个.

查看试题解析
13. 如图，在△ABC中，BD、CE是△ABC的角平分线，BD，CE交于点O.过点O作OF⊥BC，垂足为F，若∠BAC=120°，OD•OE=12，BC−BE−CD=5，则OF=.

查看试题解析
14. 如图，D为等腰Rt△ABC的斜边AB的中点，E为BC边上一点，连接ED并延长交CA的延长线于点F，过D作DH⊥EF交AC于G，交BC的延长线于H，则以下结论：①BE=CG；②DF=DH；③BH=CF；④AF=CH．其中正确的是.

查看试题解析
15. 如图，在四边形 $A B C D$ 中， $A C ⊥ B C$ 于点 $C$ ，且 $A C$ 平分 $∠ B A D$ ，若 $△ A D C$ 的面积为 $10 {cm}^{2}$ ，则 $△ A B D$ 的面积为 ${cm}^{2}$ .

查看试题解析

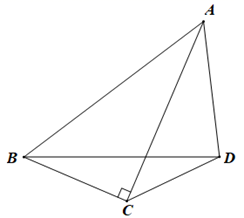
三、解答题

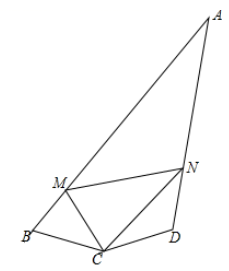
16. 如图，四边形 $A B C D$ 中， $∠ B + ∠ D = 180 °$ ， $∠ B C D = 150 °$ ， $C B = C D$ ，M、N分别为AB、AD上的动点，且 $∠ M C N = 75 °$ ．求证： $M N = B M + D N$ ．

查看试题解析
17. 如图，在 $△ A B C$ 中，∠BAC＝90°，AB＝AC ， ∠ABC的平分线交AC于点D ，过点C作BD的垂线交BD的延长线于点E ，交BA的延长线于点F ．求证：BD＝2CE ．

查看试题解析
18. （问题背景）
在四边形 $A B C D$ 中， $A B = A D$ ， $∠ B A D = 120 °$ ， $∠ B = ∠ A D C = 90 °$ ， $E$ 、 $F$ 分别是 $B C$ 、 $C D$ 上的点，且 $∠ E A F = 60 °$ ，试探究图1中线段 $B E$ 、 $E F$ 、 $F D$ 之间的数量关系．

（初步探索）

小晨同学认为：延长 $F D$ 到点 $G$ ，使 $D G = B E$ ，连接 $A G$ ，先证明 $△ A B E ≌ △ A D G$ ，再证明 $△ A E F ≌ △ A G F$ ，则可得到 $B E$ 、 $E F$ 、 $F D$ 之间的数量关系是．

（探索延伸）

在四边形 $A B C D$ 中如图2， $A B = A D$ ， $∠ B + ∠ D = 180 °$ ， $E$ 、 $F$ 分别是 $B C$ 、 $C D$ 上的点， $∠ E A F = \frac{1}{2} ∠ B A D$ ，上述结论是否仍然成立？说明理由．

（结论运用）

如图3，在某次南海海域军事演习中，舰艇甲在指挥中心（ $O$ 处）北偏西30°的 $A$ 处，舰艇乙在指挥中心南偏东70°的 $B$ 处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以80海里/小时的速度前进，舰艇乙沿北偏东50°的方向以100海里/小时的速度前进1.2小时后，指挥中心观测到甲、乙两舰艇分别到达 $E$ ， $F$ 处，且两舰艇之间的夹角（ $∠ E O F$ ）为70°，试求此时两舰艇之间的距离．

查看试题解析
19. 如图，AD是 $△ A B C$ 的角平分线，且AB>AC，E为AD上任意一点，
求证： $A B - A C > E B - E C$ .

查看试题解析

四、综合题

20. 在四边形 $A B C D$ 中.

(1)、如图1， $A B = A D$ ， $∠ A B C = ∠ A D C = 90 °$ ， $E$ ， $F$ 分别是 $B C$ ， $C D$ 上的点，且 $∠ E A F = \frac{1}{2} ∠ D A B$ ，探究图中 $E F$ ， $B E$ ， $D F$ 之间的数量关系.
小林同学探究此问题的方法是：延长 $C B$ 到点 $G$ ，使 $B G = D F$ .连接 $A G$ ，先对比 $△ A B G$ 与 $△ A D F$ 的关系，再对比 $△ A E F$ 与 $△ A E G$ 的关系，可得出 $E F$ 、 $B E$ 、 $D F$ 之间的数量关系，他的结论是；

(2)、如图2，在四边形 $A B C D$ 中， $A B = A D$ ， $∠ B + ∠ A D F = 180 °$ ， $E$ 、 $F$ 分别是 $B C$ ， $C D$ 上的点，且 $∠ E A F = \frac{1}{2} ∠ D A B$ ，则上述结论是否仍然成立，请说明理由.

(3)、如图3，在四边形 $A B C D$ 中， $∠ A B C + ∠ A D C = 180 °$ ， $A B = A D$ ，若点 $F$ 在 $C B$ 的延长线上，点 $E$ 在 $C D$ 的延长线上，若 $E F = B F + D E$ ，请写出 $∠ E A F$ 与 $∠ D A B$ 的数量关系，并给出证明过程.

查看试题解析
21. 如图

(1)、问题背景：
如图1：在四边形 $A B C D$ 中， $A B = A D$ ， $∠ B A D = 120 °$ ， $∠ B = ∠ A D C = 90 °$ .E，F分别是 $B C ， C D$ 上的点.且 $∠ E A F = 60 °$ .探究图中线段 $B E ， E F ， F D$ 之间的数量关系.小王同学探究此问题的方法是，延长 $F D$ 到点G.使 $D G = B E$ .连接 $A G$ ，先证明 $△ A B E ≌ △ A D G$ ，再证明 $△ A E F ≌ △ A G F$ ，可得出结论，他的结论应是.

(2)、探索延伸：
如图2，若在四边形 $A B C D$ 中， $A B = A D$ ， $∠ B + ∠ D = 180 °$ .E，F分别是 $B C ， C D$ 上的点，且 $∠ E A F = \frac{1}{2} ∠ B A D$ ，上述结论是否仍然成立，并说明理由.

查看试题解析
22. 在四边形ABCD中.

(1)、如图1，AB＝AD，∠ABC＝∠ADC＝90°，E，F分别是BC，CD上的点，且∠EAF＝ $\frac{1}{2}$ ∠DAB，探究图中EF，BE，DF之间的数量关系.
小林同学探究此问题的方法是：延长CB到点G，使BG＝DF.连接AG，先对比△ABG与△ADF的关系，再对比△AEF与△AEG的关系，可得出EF、BE、DF之间的数量关系，他的结论是；

(2)、如图2，在四边形ABCD中，AB＝AD，∠B+∠ADF＝180°，E、F分别是BC，CD上的点，且∠EAF＝ $\frac{1}{2}$ ∠DAB，则上述结论是否仍然成立，请说明理由.

(3)、如图3，在四边形ABCD中，∠ABC+∠ADC＝180°，AB＝AD，若点F在CB的延长线上，点E在CD的延长线上，若EF＝BF+DE，请写出∠EAF与∠DAB的数量关系，并给出证明过程.

查看试题解析
23. 【阅读理解】如图1．在 $△ A B C$ 中，若 $A B = 10$ ， $A C = 6$ ，求 $B C$ 边上的中线 $A D$ 的取值范围．解决此问题可以用如下方法：延长 $A D$ 到点E，使 $D E = A D$ ，再连接 $B E$ （或将 $△ A C D$ 绕着点D逆时针旋转 $180 °$ 得到 $△ E B D$ ），把 $A B$ ， $A C$ ， $2 A D$ 集中在 $△ A B E$ 中，

(1)、利用三角形的三边关系直接写出中线 $A D$ 的取值范围是；

(2)、【问题解决】如图2，在 $△ A B C$ 中，D是 $B C$ 边上的中点， $D E ⊥ D F$ 于点D， $D E$ 交 $A B$ 于点E， $D F$ 交 $A C$ 于点F，连接 $E F$ ，求证： $B E + C F > E F$ ；

(3)、【问题拓展】如图3，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， D为 $B C$ 边的中点，求证： $A D = \frac{1}{2} B C$ ．

查看试题解析

（人教版）2023-2024学年八年级数学上册12.2三角形全等的判定 同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年八年级数学上册12.2三角形全等的判定同步分层训练（培优卷）