(人教版)2023-2024学年八年级数学上册12.2三角形全等的判定 同步分层训练(提升卷)
试卷更新日期:2023-07-13 类型:同步测试
一、选择题
-
1. 如图是用尺规作的平分线的示意图,那么这样作图的依据是( )
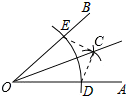 A、SSS B、SAS C、ASA D、AAS2. 如图,已知∠ACB=∠DBC,添加以下条件,不能判定△ABC≌△DCB的是( )
A、SSS B、SAS C、ASA D、AAS2. 如图,已知∠ACB=∠DBC,添加以下条件,不能判定△ABC≌△DCB的是( ) A、∠A=∠D B、AC=DB C、∠ABC=∠DCB D、AB=DC3. 如图,已知 , 以点B为圆心,适当长为半径作弧,分别交于D,P;作一条射线 , 以点F圆心,长为半径作弧l,交于点H;以H为圆心,长为半径作弧,交弧于点Q;作射线.这样可得 , 其依据是( )
A、∠A=∠D B、AC=DB C、∠ABC=∠DCB D、AB=DC3. 如图,已知 , 以点B为圆心,适当长为半径作弧,分别交于D,P;作一条射线 , 以点F圆心,长为半径作弧l,交于点H;以H为圆心,长为半径作弧,交弧于点Q;作射线.这样可得 , 其依据是( ) A、 B、 C、 D、4. 如图,将两块大小相同的三角板(∠B=∠C=30°的直角三角形)按图中所示的位置摆放.若BE交CF于点D交AC于点M,AB交CF于点N,则下列结论:①∠EAM=∠FAN;②△ACN≌△ABM;③∠EAF+∠BAC=120°;④EM=FN;⑤CF⊥BE中,正确的结论有( )
A、 B、 C、 D、4. 如图,将两块大小相同的三角板(∠B=∠C=30°的直角三角形)按图中所示的位置摆放.若BE交CF于点D交AC于点M,AB交CF于点N,则下列结论:①∠EAM=∠FAN;②△ACN≌△ABM;③∠EAF+∠BAC=120°;④EM=FN;⑤CF⊥BE中,正确的结论有( ) A、5个 B、4个 C、3个 D、2个5. 如图,点E、F在线段AC上,AF=CE,AD=CB,下列不能推断△ADF≌△CBE是( )
A、5个 B、4个 C、3个 D、2个5. 如图,点E、F在线段AC上,AF=CE,AD=CB,下列不能推断△ADF≌△CBE是( ) A、∠D=∠B B、∠A=∠C C、BE=DF D、AD//BC6. 如图,小亮进行以下操作:以点A为圆心,适当长为半径作圆弧分别交AB, AC于点D,E;分别以点D,E为圆心,大于DE长为半径作圆弧,两条圆弧交于∠BAC内一点F,作射线AF.若∠BDF=50°,∠EFD-∠BAC=24°,则∠BAC等于( )
A、∠D=∠B B、∠A=∠C C、BE=DF D、AD//BC6. 如图,小亮进行以下操作:以点A为圆心,适当长为半径作圆弧分别交AB, AC于点D,E;分别以点D,E为圆心,大于DE长为半径作圆弧,两条圆弧交于∠BAC内一点F,作射线AF.若∠BDF=50°,∠EFD-∠BAC=24°,则∠BAC等于( ) A、26° B、31° C、37° D、38°7. 如图,已知 , 添加下列条件不能判定的是( )
A、26° B、31° C、37° D、38°7. 如图,已知 , 添加下列条件不能判定的是( ) A、 B、 C、 D、8. 如图,在中, , , , 一条线段 , , 两点分别在线段和的垂线上移动,若以 , , 为顶点的三角形与以 , , 为顶点的三角形全等,则的值为( )
A、 B、 C、 D、8. 如图,在中, , , , 一条线段 , , 两点分别在线段和的垂线上移动,若以 , , 为顶点的三角形与以 , , 为顶点的三角形全等,则的值为( ) A、6cm B、12cm C、12cm或6cm D、以上答案都不对9. 小华同学周末在家做家务,不慎把家里的一块三角形玻璃打碎成如图所示的四块,现在要去玻璃店配一块完全一样的玻璃,可以选择的方法是( )
A、6cm B、12cm C、12cm或6cm D、以上答案都不对9. 小华同学周末在家做家务,不慎把家里的一块三角形玻璃打碎成如图所示的四块,现在要去玻璃店配一块完全一样的玻璃,可以选择的方法是( ) A、带①②去 B、带②③去 C、带③④去 D、带②④去10. 如图, , 于 , 于E,与交于点 . 有下列结论:
A、带①②去 B、带②③去 C、带③④去 D、带②④去10. 如图, , 于 , 于E,与交于点 . 有下列结论:①;②;③点在的平分线上;④点在的中垂线上.以上结论正确的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,已知 , 若以“”判定 , 需添加的条件是
 12. 如图,已知 AB//CF,E为DF的中点,若AB=13cm,CF=7cm,则BD=cm .
12. 如图,已知 AB//CF,E为DF的中点,若AB=13cm,CF=7cm,则BD=cm . 13. 如图,在中, , 于点D,于点C, . 点E,点F分别在线段上, , 连接 .
13. 如图,在中, , 于点D,于点C, . 点E,点F分别在线段上, , 连接 . (1)、图中与相等的线段是;(2)、当取最小值时°14. 如图,点D,E分别在线段上,与相交于O点,已知 , 添加一个条件能直接用“”判定 , 符合要求的条件是 .
(1)、图中与相等的线段是;(2)、当取最小值时°14. 如图,点D,E分别在线段上,与相交于O点,已知 , 添加一个条件能直接用“”判定 , 符合要求的条件是 . 15. 在中,已知 , 的平分线与的平分线相交于点O,的平分线交于F,则:
15. 在中,已知 , 的平分线与的平分线相交于点O,的平分线交于F,则: (1)、的度数是 .(2)、若 , , 则的长是 .
(1)、的度数是 .(2)、若 , , 则的长是 .三、解答题
-
16. 已知:如图,点在同一条直线上,.求证:.
 17. 如图,点在同一直线上, , 求证:.
17. 如图,点在同一直线上, , 求证:. 18. 如图,已知在和中,.求证:.
18. 如图,已知在和中,.求证:.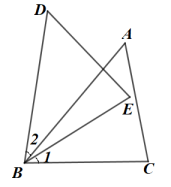 19. 如图,A,D两点在所在直线同侧, , 垂足分别为A,D.的交点为E, . 求证: .
19. 如图,A,D两点在所在直线同侧, , 垂足分别为A,D.的交点为E, . 求证: .
四、综合题
-
20. 如图,在△ABC中,D是AB上一点,CF//AB,DF交AC于点E,.
 (1)、求证:(2)、若 , , 求BD的长.21. 在中, , 直线经过点C,且于D,于E.
(1)、求证:(2)、若 , , 求BD的长.21. 在中, , 直线经过点C,且于D,于E. (1)、当直线绕点C旋转到图1的位置时,求证:
(1)、当直线绕点C旋转到图1的位置时,求证:①;
② .
(2)、当直线绕点C旋转到图2的位置时,求证:;(3)、当直线绕点C旋转到图3的位置时,试问具有怎样的等量关系?请写出这个等量关系,并加以证明.22. 阅读下面材料:小明遇到这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系.小明发现,在BC上截取CA′=CA,连接DA′,从而将问题解决(如图2).
 (1)、求证:△ADC≌△A′DC;(2)、试猜想写出BC和AC、AD之间的数量关系,并给出证明.23. 如图
(1)、求证:△ADC≌△A′DC;(2)、试猜想写出BC和AC、AD之间的数量关系,并给出证明.23. 如图 (1)、证明角平分线具有的性质:角平分线上的点到角的两边的距离相等.为了更直观、清楚地表达题意,我们通常在证明之前画出图形,并用符号表示已知和求证.如图1,已知:平分 , 点在上, , , 垂足分别为 , . 求证: .(2)、如图2,在中,平分 , 交于点 , 于点 , 于点 , , 若 , 求的长.
(1)、证明角平分线具有的性质:角平分线上的点到角的两边的距离相等.为了更直观、清楚地表达题意,我们通常在证明之前画出图形,并用符号表示已知和求证.如图1,已知:平分 , 点在上, , , 垂足分别为 , . 求证: .(2)、如图2,在中,平分 , 交于点 , 于点 , 于点 , , 若 , 求的长.