广东省阳江市江城区2022-2023学年八年级第二学期数学期末试题

试卷更新日期：2023-07-13 类型：期末考试

进入出卷网下载

一、选择题:本大题共10小题，每小题3分，共30分.在每小题列出的四个选项中，只有一项是符合题目要求的.

1. 要使式子 $\sqrt{x + 4}$ 有意义，则 $x$ 必须满足（）

A、 $x ⩾ 0$ B、 $x \neq - 4$ C、 $x ⩾ - 4$ D、 $x > - 4$

查看试题解析
2. 下列四个图象中， $y$ 不是 $x$ 的函数的是（）

A、 B、 C、 D、

查看试题解析
3. 为庆祝中国共产党建党102周年，某校开展主题为《党在我心中》的绘画、书法、摄影等艺术作品征集活动，从八年级5个班收集到的作品数量(单位：件)分别为50、45、42、46、50，则这组数据的众数是（）

A、46 B、45 C、50 D、42

查看试题解析
4. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{\frac{1}{14}}$ B、 $\sqrt{14}$ C、 $\sqrt{0.1}$ D、 $\sqrt{50}$

查看试题解析
5. 双减政策落地，各地学校大力提升学生核心素养，学生的综合评价含文化课、体育和艺术三部分，文化课成绩、体育成绩与艺术成绩按5：3：2计入综合评价，若宸宸文化课成绩为90分，体育成绩为80分，艺术成绩为85分，则他的综合评价得分为（）

A、84 B、85 C、86 D、87

查看试题解析
6. 已知 $△ A B C$ 中，a、b、c分别是 $∠ A 、 ∠ B 、 ∠ C$ 的对边，下列条件中不能判断 $△ A B C$ 是直角三角形的是（）

A、 $∠ A = ∠ C - ∠ B$ B、 $a^{2} = b^{2} - c^{2}$ C、 $a = 3 ， b = 5 ， c = 4$ D、 $a ： b ： c = 2 ： 3 ： 4$

查看试题解析
7. 平行四边形的周长为24，相邻两边的差为2，则平行四边形的各边长为（）．

A、4，4，8，8 B、5，5，7，7 C、5.5，5.5，6.5，6.5 D、3，3，9，9

查看试题解析
8. 在函数 $y = - 2 x + b$ 的图象上有 $A (1 ， y_{1}) ， B (- 2 ， y_{2})$ 两个点，则下列各式中正确的是（）

A、 $y_{1} < y_{2}$ B、 $y_{1} ⩽ y_{2}$ C、 $y_{1} > y_{2}$ D、 $y_{1} ⩾ y_{2}$

查看试题解析
9. 如图，所有四边形都是正方形，所有三角形都是直角三角形，若正方形A、B、D的面积依次为6、10、24，则正方形 $C$ 的面积为（）

A、4 B、6 C、8 D、12

查看试题解析
10. 如图，正方形ABCD的面积为1， $△ A B E$ 是等边三角形，点 $E$ 在正方形ABCD内，在对角线AC上有一点 $P$ ，使 $P D + P E$ 的和最小，则这个最小值为（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、不能确定

查看试题解析

二、填空题:本大题共5小题，每小题3分，共15分.请将下列各题的正确答案填写在答题卡相应的位置上.

11. 已知 $a$ 为正整数，且 $\sqrt{12 a}$ 也为正整数，则 $a$ 的最小值为.

查看试题解析
12. 甲、乙两个芭蕾舞团的女学员身高的方差分别是 $s_{甲}^{2} = 1.5$ 、 $s_{乙}^{2} = 2.5$ ，则女学员身高更整齐的是芭蕾舞团（填“甲”或“乙”）．

查看试题解析
13. 在菱形ABCD中，对角线AC和BD相交于点 $O ， A C = 4 c m ， B D = 8 c m$ ，则这个菱形的面积是 $c m^{2}$ .

查看试题解析
14. 将直线 $y = 2 x$ 向上平移5个单位，得到直线的解析式.

查看试题解析
15. 如图1，在矩形ABCD中， $A B > A D$ ，对角线AC，BD相交于点 $O$ ，动点 $P$ 由点 $A$ 出发，沿 $A \to B \to C$ 运动.设点 $P$ 的运动路程为 $x ， △ A O P$ 的面积为y，y与 $x$ 的函数关系图象如图(2)所示，则BC边的长为.

查看试题解析

三、解答题(一):本大题共3小题，每小题8分，共24分.

16. 计算： $\sqrt{48} \div \sqrt{2} - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{(- 2)^{2}} - | 2 - \sqrt{6} |$ .

查看试题解析
17. 如图，在平行四边形ABCD中，点E、F分别在BC、AD上，且 $B E = D F$ .请判断AE与CF的数量关系，并说明理由.

查看试题解析
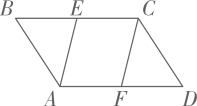18. 已知，直线y=kx+b与直线 $y = \frac{1}{2} x$ 相交于点 $P (2 ， m)$ ，与 $x$ 轴、 $y$ 轴分别交于点A、B，点 $B$ 的坐标为 $(0 ， 2)$ .求直线 $y = k x + b$ 的函数解析式及点 $A$ 的坐标.

查看试题解析

四、解答题(二):本大题共3小题，每小题9分，共27分.

19. 为切实做好校内“午托”工作，某学校食堂为参加“午托”的学生提供了四种价格的午餐供其选择，四种价格分别是A：6元；B：7元；C：8元；D：10元.为了解学生对四种午餐的购买情况，学校随机抽样调查了一部分学生某天四种午餐的购买情况，依统计数据绘制成了如下两幅尚不完整的统计图，根据图中信息解决下列问题：

(1)、求被抽查的学生人数及m的值，并补全条形统计图；

(2)、被抽查学生购买午餐费用的平均价为，众数为，中位数为；

(3)、若该校参加“午托”的学生有1200人，请估计购买7元午餐的学生有多少人?

查看试题解析
20. 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》；“平地秋千未起，踏板一尺离地。行二步恰竿齐，五尺板高离地…”翻译成现代文为：如图，秋千OA静止的时候，踏板离地高一尺(AC=1尺)，将它往前推进两步（EB=10尺)，此时踏板升高离地五尺（BD=5尺)，求秋千绳索（OA或OB）的长度.

查看试题解析
21. 为响应国家“全民阅读，建设学习型社会”的倡议，营造读书好，好读书，读好书的氛围，某校图书馆购进甲、乙两种图书，已知甲、乙两种图书的单价分别是25元和8元．

(1)、学校第一次购买甲、乙两种图书共100本，且恰好支出1820元，求第一购买了甲、乙两种图书各多少本？

(2)、若学校准备再次购买甲、乙两种图书共210本，且甲种图书的数量不低于乙种图书数量的一半，请问怎么购买费用最少？最少费用是多少元？

查看试题解析

五、解答题(三):本大题共2小题，每小题12分，共24分.

22. 如图，在 $□ A B C D$ 中，AC，BD相交于点 $O ， A B = A D ， A C = 8 ， B D = 6 ， C E / / B D ， B E / /$ AC，连接OE，BC与OE相交于点 $P$ ，连接DP.

(1)、求AB的长；

(2)、求证： OE=AD ；

(3)、求DP的长.

查看试题解析
23. 如图，在平面直角坐标系中，直线 $l_{1} ： y = - x + 5$ 与 $y$ 轴交于点 $A$ ，直线 $l_{2}$ 与 $x$ 轴、 $y$ 轴分别交于点 $B (- 4 ， 0)$ 和点 $C$ ，且与直线 $l_{1}$ 交于点 $D (2 ， m)$ .

(1)、求直线 $l_{2}$ 的解析式；

(2)、若点 $E$ 为线段BC上一个动点，过点 $E$ 作 $E F ⊥ x$ 轴，垂足为 $F$ ，且与直线 $l_{1}$ 交于点 $G$ ，当 $E G = 6$ 时，求点 $G$ 的坐标；

(3)、若在平面上存在点 $H$ ，使得以点A，C，D，H为顶点的四边形是平行四边形，请直接写出点 $H$ 的坐标.

查看试题解析