广西柳州市2022-2023学年八年级下册数学期末考试质量监测卷

试卷更新日期：2023-07-13 类型：期末考试

进入出卷网下载

一、选择题（本题共10小题，每小题3分，满分30分。在每个小题给出的四个选项中，只有一项是正确的，每小题选对得3分，选错、不选或多选均得零分，请把选择题的答案填入下面的表格中）

1. 二次根式 $\sqrt{x - 2}$ 有意义的条件是（）

A、 $x ⩾ 2$ B、 $x < 2$ C、 $x > 2$ D、 $x ⩽ 2$

查看试题解析
2. 下列各组数中能作为直角三角形的三边长的是（　　）

A、1，2，3 B、3，4，5 C、4，5，6 D、7，8，9

查看试题解析
3. 下列计算结果正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 $3 \sqrt{2} - \sqrt{2} = 3$ C、 $\frac{\sqrt{6}}{\sqrt{3}} = 2$ D、 ${(- \sqrt{5})}^{2} = 5$

查看试题解析
4. 若一次函数 $y = x + 4$ 的图象上有两点 $A (- \frac{1}{2} ， y_{1}) 、 B (1 ， y_{2})$ ，则下列说法正确的是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} ⩾ y_{2}$ C、 $y_{1} < y_{2}$ D、 $y_{1} ⩽ y_{2}$

查看试题解析
5. 一次函数 $y = - x + 1$ 的图象不经过的象限是 $($ ）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 如图，四边形ABCD的对角线AC和BD交于点 $O$ ，则下列不能判断四边形ABCD是平行四边形的条件是（）

A、 $A B = D C ， A D = B C$ B、 $O A = O C ， O B = O D$ C、 $A D = B C ， A D / / B C$ D、 $A B = C D ， A D / / B C$

查看试题解析
7. 如图，在平面直角坐标系中， $▱ A B C D$ 的顶点A，B，D的坐标分别是 $(0 ， 0) ， (5 ， 0) ， (2 ， 3)$ ，则顶点 $C$ 的坐标是（）

A、 $(7 ， 3)$ B、 $(5 ， 3)$ C、 $(3 ， 7)$ D、 $(8 ， 2)$

查看试题解析
8. 如图，在Rt $△ A B C$ 中， $∠ A C B = 9 0^{°}$ ，分别以AC、BC为边作正方形，若 $A B = 12$ ，则正方形ADEC和正方形BCFG的面积和为（）

A、144 B、120 C、100 D、无法计算

查看试题解析
9. 如图为一次函数y=kx+b（k和 $b$ 为常数且 $k \neq 0 ， b \neq 0$ ）的图象，则一次函数 $y = b x + k$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在四边形ABCD中， $A D = B C ， ∠ D A B = 5 0^{°} ， ∠ C B A = 7 0^{°} ， P 、 M 、 N$ 分别是AB、AC、BD的中点，若 $B C = 8$ .则 $△ P M N$ 的周长是（）

A、10 B、12 C、16 D、18

查看试题解析

二、填空题（每小题3分，共18分）

11. 计算： $\sqrt{9}$ = ．

查看试题解析
12. 将直线 $y = 2 x$ 向下平移2个单位长度，所得直线的函数解析式是.

查看试题解析
13. 甲、乙两名射击运动员10次射击训练成绩的方差为 $S_{甲}^{2} = 1.5$ ， $S_{乙}^{2} = 1.8$ ，则运动员的成绩比较稳定（填甲或乙）.

查看试题解析
14. 如图，矩形ABCD的对角线相交于点 $O ， A B = 3 ， A D = 4$ ，则线段AO的长度为.

查看试题解析
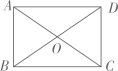15. 如图，在Rt $△ A B C$ 中， $∠ C = 9 0^{°} ， A C = 3 ， B C = 5$ ，分别以A，B为圆心，大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧交点分别为点P，Q，过P，Q两点作直线交BC于点 $D$ ，则线段CD的长是.

查看试题解析
16. 已知一次函数 $y_{1} = k x + 2$ （ $k$ 为常数， $k \neq 0) ， y_{2} = x - 3$ ，若当 $x < 1$ 时有 $y_{1} > y_{2}$ ，则 $k$ 的取值范围是.

查看试题解析

三、解答题（本题共7小题，满分52分，解答时应写出必要的文字说明、演算步骤或推理过程）

17. 计算： $\sqrt{24} \div \sqrt{3} - \sqrt{2}$

查看试题解析
18. 如图，四边形ABCD的对角线AC、BD相交于点 $O$ ，且 $A B = A D ， A D / / B C$ ， $O A = O C$ .求证：四边形 $A B C D$ 是菱形.

查看试题解析
19. 如图，在平面直角坐标系中， $O$ 为坐标原点，一次函数 $y = k x + 2$ （ $k$ 为常数， $k \neq 0)$ 的图象经过 $A (- 2 ， - 1)$ ，并且交 $x$ 轴于点 $B$ ，交 $y$ 轴于点 $C$ .

(1)、求 $k$ 的值；

(2)、求 $△ B O C$ 的面积.

查看试题解析
20. 某校为了了解九年级男生的体能情况，规定参加测试的每名男生从“仰卧起坐”、“引体向上”、“耐力跑1000米”三个项目中随机抽取一项作为测试项目.

(1)、九（1）班的全体25名男生积极参加本次活动，具体各项测试项目的统计结果如图所示，则参加“引体向上”测试的男生有名；

(2)、九（1）班所有参加“耐力跑1000米”测试的8名男生的成绩分别为：（单位：分）100，82，90，95，82，90，95，90.
①九（1）班所有参加“耐力跑1000米”测试的男生成绩的中位数是分；

②如果将不低于90分的成绩评为优秀，请你估计该校九年级抽中“耐力跑1000米”的160名男生的成绩为优秀的约有多少人?

查看试题解析
21. 我国明代有一位杰出的数学家提出一道“荡秋千”的数学问题：“平地秋千末起，踏板一尺离地，送行二步与人齐，五尺人高曾记；仕女佳人争蹴，终朝笑语欢嬉，良工高士素好奇，算出索长有几？”其意思为：如图，当秋千静止在地面上时，秋千的踏板离地的距离为一尺（ $C E = 1$ 尺），将秋千的踏板往前推两步（每一步合五尺，即 $E F = 10$ 尺），秋千的踏板离地面的距离与人一样高，这个人的身高为五尺（ $D F = 5$ 尺），求这个秋千的绳索AC的长.

查看试题解析
22. 阅读下面的材料并解决问题.
      $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$

      $\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$

      $\frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$

……

(1)、观察上式并填空： $\frac{1}{\sqrt{6} + \sqrt{5}} =$ .

(2)、观察上式并猜想：当n是正整数时， $\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ ；（用含 $n$ 的式子表示）

(3)、请利用（2）的结论计算下列式子：
      $(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \dots \dots + \frac{1}{\sqrt{2022} + \sqrt{2021}} + \frac{1}{\sqrt{2023} + \sqrt{2022}}) \times (\sqrt{2023} + 1)$

查看试题解析
23. 如图，在平面直角坐标系中， $O$ 为坐标原点，正方形OABC的OA、OC边分别在 $x$ 轴、 $y$ 轴上，其中 $O A = 4 ， D$ 为射线CA上一动点，以BD为边向右作正方形BDMN（整个正方形位于直线AC的右侧）.

(1)、求A、C两点所在的直线解析式.

(2)、当点D是线段AC的中点时，点 $N$ 的坐标为.（直接写出结果，不用写解题过程）

(3)、连接AN，当 $A D = \frac{1}{3} A N$ 时，求此时点 $N$ 的坐标。

查看试题解析